Vector Calculus & Partial Differential Equations (2/2)
https://www.youtube.com/playlist?list=PLMrJAkhIeNNQromC4WswpU1krLOq5Ro6S
Partial Differential Equations Overview

Laplace's Equation and Poisson's Equation

Deriving the Heat Equation: A Parabolic Partial Differential Equation for Heat Energy Conservation

The Heat Equation and the Steady State Heat Distribution via Laplace's Equation

Deriving the Heat Equation in 2D & 3D (& in N Dimensions!) with Control Volumns and Vector Calculus

Separation of Variables! ...or how I learned to stop worring and solve Laplace's equation :)
"We have all traveled through time and space to be here.."
교수님께서 너무 멋진 표현을 쓰셨다 ^^
PDE가 rate of change in time, space를 describing한다는 것에 비유하신 것 같다.



We have introduced one of the most powerful methods of solving partial differential equations which is separation of variables and it allows us to transform partial differential equation into two systems of ordinary differential equations. You get a set of ordinary differential equations in x and you get a system of ordinary differential equations in y. And we know how to solve ordinary differential equations they're relatively easy, especially linear ODEs that are second order, all of our solutions are going to be exponentials or sines and cosines.
Step zero is assume you can split your variables. Step one is plug it into your PDE and derive a system of ODEs out. The next step two is pick the one that has easy boundary conditions, and find the special values of lambda, the special constants lambda that allow you to satisfy those boundary conditions, those special lambdas are actually eigenvalues of this ordinary differential equation that satisfy these boundary conditions. So we have eigenvalues lambda and the corresponding eigen functions.
I have countably many eigenvalues lambda that satisfy these boundary conditions and corresponding eigenfunctions. So I used to have eigenvalues and eigenvectors, but now we have eigenfunctions because the solutions are functions, we live in a function space, a hilbert space.
Step three, now that we have determined those special lambdas, plug those into our hard differential equation with hard boundary conditions.
마지막에 hard boundary condition 만족하는 coefficient An은 fourier transform으로 도출.
Deriving the Wave Equation

진지하게 수업 듣다가 빵 터졌다.
wave equation 설명하시는데 진짜 기타 들고 오셨다. ㅎㅎㅎ
교수님 열정 감사합니다. 진짜 이해 잘되요!


Solving the Wave Equation with Separation of Variables... and Guitar String Physics

Guitar string으로 설명해주시는데 진짜 이해 잘 된다..!!
wave equation 다른 강의를 안 들어봐서 모르겠지만, 교수님 설명 정말 잘 해주시는 거 같다.
넘나 감사 ㅠㅠㅠㅠ
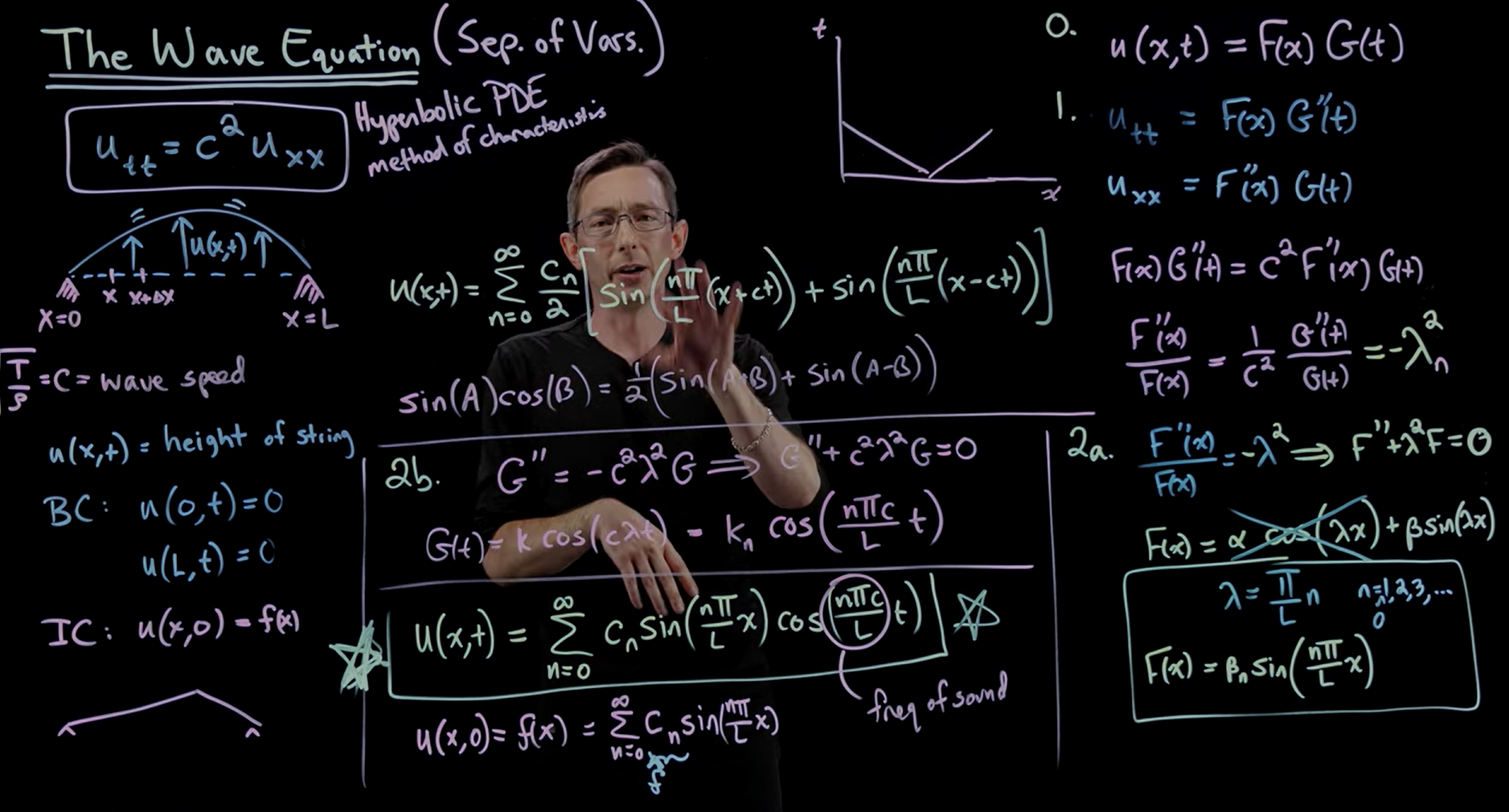
The Method of Characteristics and the Wave Equation


Solving PDEs with the Laplace Transform: The Heat Equation

Solving PDEs with the Laplace Transform: The Wave Equation
