Fourier Analysis (& Wavelets)
https://www.youtube.com/playlist?list=PLMrJAkhIeNNT_Xh3Oy0Y4LTj0Oxo8GqsC
Fourier Series


Inner Products in Hilbert Space

Complex Fourier Series

Fourier Series and Gibbs Phenomena

The Fourier Transform

The Fourier Transform and Derivatives

The Fourier Transform and Convolution Integrals

Parseval's Theorem

Solving the Heat Equation with the Fourier Transform

The Discrete Fourier Transform (DFT)

The Fast Fourier Transform Algorithm

Denoising Data with FFT

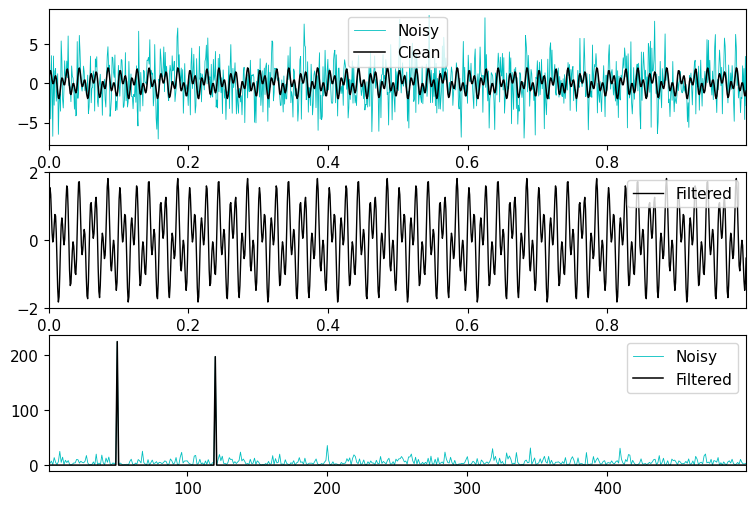
Computing Derivatives with FFT


Solving PDEs with the FFT






The Spectrogram and the Gabor Transform

Spectrogram Examples


Uncertainty Principles and the Fourier Transform

Wavelets and Multiresolution Analysis
kernel filtering으로 multi-resolution decompose해서 feature를 extract하고 compress한다는 점에서 CNN operation과 닮았다.

Image Compression and the FFT / Wavelets
--------------------------------------------------------------------------------------------------------------------
FFT로 image compression을 하는 원리가, most of fourier coefficient가 매우 작기 때문에 truncation 하여도 거의 quality에 영향을 주지 않기 때문인데, 이건 ML/DL vision에서 manifold hypothesis의 내용과도 상통한다.
사실 image의 data distribution은 극히 작은 영역에 reside하고 있고 대부분의 embient space는 거의 zero에 가깝다.
이게 image quantization, tokenization에서 소수의 token으로도 image를 high-quality로 표현할 수 있다는 것과도 상관이 있는 건가? (이 논문을 보고 싶었는데, keep 해놨는데 다시 찾아봐야지) (- An Image is Worth 32 Tokens for Reconstruction and Generation)
--------------------------------------------------------------------------------------------------------------------
"The Parseval's theorem says that there's a relationship between the energy in fourier space and the energy in signal in pixel space. So if I'm only throwing away a lot of Fourier coefficients, 99% of the Fourier coefficients, but the ones I'm throwing away are so small that they don't actually change the norm or the energy of this signal very much. Because I'm only throwing away the ones that are almost zero anyway.
So Parseval's theorem tells me is that if I only threshold the very small Fourier coefficients, it has negligible degradation of my original image.
This is basis of all image compression and audio compression.
When you Fourier transform your image or audio signal, most of those Fourier coefficients are very very small, negligibly small. And because the Parseval's theorem, if I zero out those small Fourier coefficients, and I only keep the largest ones which oftentimes is only 1% or 2% of these Fourier coefficients, if I only keep those, then when I inverse fourier transform, the image looks identical to the original, full resolution image.

The Laplace Transform: A Generalized Fourier Transform

Laplace Transform Examples

Laplace Transforms and Differential Equations
