Score-based Generative Modeling through Stochastic Differential Equations
https://arxiv.org/pdf/2011.13456
https://github.com/yang-song/score_sde
(Feb 2021 ICLR 2021)
Abstract
Creating noise from data is easy; creating data from noise is generative modeling. We present a stochastic differential equation (SDE) that smoothly transforms a complex data distribution to a known prior distribution by slowly injecting noise, and a corresponding reverse-time SDE that transforms the prior distribution back into the data distribution by slowly removing the noise. Crucially, the reverse-time SDE depends only on the time-dependent gradient field (a.k.a., score) of the perturbed data distribution. By leveraging advances in score-based generative modeling, we can accurately estimate these scores with neural networks, and use numerical SDE solvers to generate samples. We show that this framework encapsulates previous approaches in score-based generative modeling and diffusion probabilistic modeling, allowing for new sampling procedures and new modeling capabilities. In particular, we introduce a predictor-corrector framework to correct errors in the evolution of the discretized reverse-time SDE. We also derive an equivalent neural ODE that samples from the same distribution as the SDE, but additionally enables exact likelihood computation, and improved sampling efficiency. In addition, we provide a new way to solve inverse problems with score-based models, as demonstrated with experiments on class-conditional generation, image inpainting, and colorization. Combined with multiple architectural improvements, we achieve record-breaking performance for unconditional image generation on CIFAR-10 with an Inception score of 9.89 and FID of 2.20, a competitive likelihood of 2.99 bits/dim, and demonstrate high fidelity generation of 1024 × 1024 images for the first time from a score-based generative model.
1. Introduction
Two successful classes of probabilistic generative models involve sequentially corrupting training data with slowly increasing noise, and then learning to reverse this corruption in order to form a generative model of the data. Score matching with Langevin dynamics (SMLD) (Song & Ermon, 2019) estimates the score (i.e., the gradient of the log probability density with respect to data) at each noise scale, and then uses Langevin dynamics to sample from a sequence of decreasing noise scales during generation. Denoising diffusion probabilistic modeling (DDPM) (Sohl-Dickstein et al., 2015; Ho et al., 2020) trains a sequence of probabilistic models to reverse each step of the noise corruption, using knowledge of the functional form of the reverse distributions to make training tractable. For continuous state spaces, the DDPM training objective implicitly computes scores at each noise scale. We therefore refer to these two model classes together as score-based generative models.
Score-based generative models, and related techniques (Bordes et al., 2017; Goyal et al., 2017; Du & Mordatch, 2019), have proven effective at generation of images (Song & Ermon, 2019; 2020; Ho et al., 2020), audio (Chen et al., 2020; Kong et al., 2020), graphs (Niu et al., 2020), and shapes (Cai et al., 2020). To enable new sampling methods and further extend the capabilities of score-based generative models, we propose a unified framework that generalizes previous approaches through the lens of stochastic differential equations (SDEs).
Specifically, instead of perturbing data with a finite number of noise distributions, we consider a continuum of distributions that evolve over time according to a diffusion process. This process progressively diffuses a data point into random noise, and is given by a prescribed SDE that does not depend on the data and has no trainable parameters. By reversing this process, we can smoothly mold random noise into data for sample generation. Crucially, this reverse process satisfies a reverse-time SDE (Anderson, 1982), which can be derived from the forward SDE given the score of the marginal probability densities as a function of time. We can therefore approximate the reverse-time SDE by training a time-dependent neural network to estimate the scores, and then produce samples using numerical SDE solvers. Our key idea is summarized in Fig. 1.

Our proposed framework has several theoretical and practical contributions:
Flexible sampling and likelihood computation:
We can employ any general-purpose SDE solver to integrate the reverse-time SDE for sampling. In addition, we propose two special methods not viable for general SDEs: (i) Predictor-Corrector (PC) samplers that combine numerical SDE solvers with score-based MCMC approaches, such as Langevin MCMC (Parisi, 1981) and HMC (Neal et al., 2011); and (ii) deterministic samplers based on the probability flow ordinary differential equation (ODE). The former unifies and improves over existing sampling methods for score-based models. The latter allows for fast adaptive sampling via black-box ODE solvers, flexible data manipulation via latent codes, a uniquely identifiable encoding, and notably, exact likelihood computation.
Controllable generation:
We can modulate the generation process by conditioning on information not available during training, because the conditional reverse-time SDE can be efficiently estimated from unconditional scores. This enables applications such as class-conditional generation, image inpainting, colorization and other inverse problems, all achievable using a single unconditional score-based model without re-training.
Unified framework:
Our framework provides a unified way to explore and tune various SDEs for improving score-based generative models. The methods of SMLD and DDPM can be amalgamated into our framework as discretizations of two separate SDEs. Although DDPM (Ho et al., 2020) was recently reported to achieve higher sample quality than SMLD (Song & Ermon, 2019; 2020), we show that with better architectures and new sampling algorithms allowed by our framework, the latter can catch up—it achieves new state-of-the-art Inception score (9.89) and FID score (2.20) on CIFAR-10, as well as high-fidelity generation of 1024 × 1024 images for the first time from a score-based model. In addition, we propose a new SDE under our framework that achieves a likelihood value of 2.99 bits/dim on uniformly dequantized CIFAR-10 images, setting a new record on this task.
2. Background
2.1. Denoising Score Matching with Langevin Dynamics (SMLD)


2.2. Denoising Diffusion Probabilistic Models (DDPM)

3. Score-based Generative Modeling with SDEs
Perturbing data with multiple noise scales is key to the success of previous methods. We propose to generalize this idea further to an infinite number of noise scales, such that perturbed data distributions evolve according to an SDE as the noise intensifies. An overview of our framework is given in Fig. 2.

3.1. Perturbing Data with SDEs


3.2. Generating Samples by Reversing the SDE

3.3. Estimating Scores for the SDE


3.4. Examples: VE, VP SDEs and Beyond


4. Solving the Reverse SDE
After training a time-dependent score-based model sθ, we can use it to construct the reverse-time SDE and then simulate it with numerical approaches to generate samples from p0.
4.1. General-Purpose Numerical SDE Solvers
Numerical solvers provide approximate trajectories from SDEs. Many general-purpose numerical methods exist for solving SDEs, such as Euler-Maruyama and stochastic Runge-Kutta methods (Kloeden & Platen, 2013), which correspond to different discretizations of the stochastic dynamics. We can apply any of them to the reverse-time SDE for sample generation.
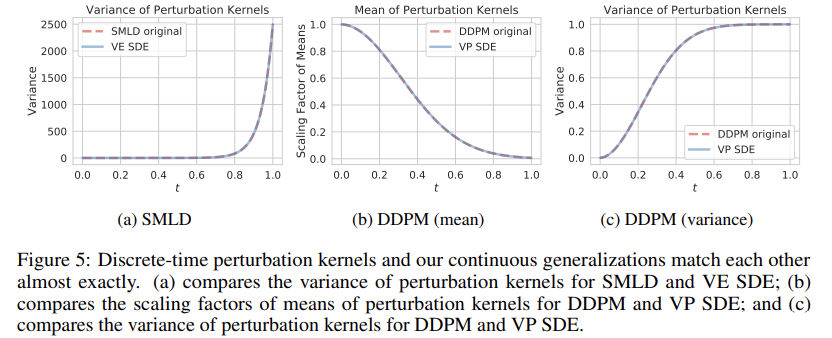
Ancestral sampling, the sampling method of DDPM (Eq. (4)), actually corresponds to one special discretization of the reverse-time VP SDE (Eq. (11)) (see Appendix E). Deriving the ancestral sampling rules for new SDEs, however, can be non-trivial. To remedy this, we propose reverse diffusion samplers (details in Appendix E), which discretize the reverse-time SDE in the same way as the forward one, and thus can be readily derived given the forward discretization. As shown in Table 1, reverse diffusion samplers perform slightly better than ancestral sampling for both SMLD and DDPM models on CIFAR-10 (DDPM-type ancestral sampling is also applicable to SMLD models, see Appendix F.)

4.2. Predictor-Corrector Samplers
Unlike generic SDEs, we have additional information that can be used to improve solutions. Since we have a score-based model sθ*(x, t) =∇x log pt(x), we can employ score-based MCMC approaches, such as Langevin MCMC (Parisi, 1981; Grenander & Miller, 1994) or HMC (Neal et al., 2011) to sample from pt directly, and correct the solution of a numerical SDE solver.
Specifically, at each time step, the numerical SDE solver first gives an estimate of the sample at the next time step, playing the role of a “predictor”. Then, the score-based MCMC approach corrects the marginal distribution of the estimated sample, playing the role of a “corrector”. The idea is analogous to Predictor-Corrector methods, a family of numerical continuation techniques for solving systems of equations (Allgower & Georg, 2012), and we similarly name our hybrid sampling algorithms Predictor-Corrector (PC) samplers. Please find pseudo-code and a complete description in Appendix G. PC samplers generalize the original sampling methods of SMLD and DDPM: the former uses an identity function as the predictor and annealed Langevin dynamics as the corrector, while the latter uses ancestral sampling as the predictor and identity as the corrector.
We test PC samplers on SMLD and DDPM models (see Algorithms 2 and 3 in Appendix G) trained with original discrete objectives given by Eqs. (1) and (3). This exhibits the compatibility of PC samplers to score-based models trained with a fixed number of noise scales. We summarize the performance of different samplers in Table 1, where probability flow is a predictor to be discussed in Section 4.3. Detailed experimental settings and additional results are given in Appendix G. We observe that our reverse diffusion sampler always outperform ancestral sampling, and corrector-only methods (C2000) perform worse than other competitors (P2000, PC1000) with the same computation (In fact, we need way more corrector steps per noise scale, and thus more computation, to match the performance of other samplers.) For all predictors, adding one corrector step for each predictor step (PC1000) doubles computation but always improves sample quality (against P1000). Moreover, it is typically better than doubling the number of predictor steps without adding a corrector (P2000), where we have to interpolate between noise scales in an ad hoc manner (detailed in Appendix G) for SMLD/DDPM models. In Fig. 9 (Appendix G), we additionally provide qualitative comparison for models trained with the continuous objective Eq. (7) on 256 × 256 LSUN images and the VE SDE, where PC samplers clearly surpass predictor-only samplers under comparable computation, when using a proper number of corrector steps.
4.3. Probability Flow and Connection to Neural ODEs




4.4. Architecture Improvements
We explore several new architecture designs for score-based models using both VE and VP SDEs (details in Appendix H), where we train models with the same discrete objectives as in SMLD/DDPM. We directly transfer the architectures for VP SDEs to sub-VP SDEs due to their similarity. Our optimal architecture for the VE SDE, named NCSN++, achieves an FID of 2.45 on CIFAR-10 with PC samplers, while our optimal architecture for the VP SDE, called DDPM++, achieves 2.78.
By switching to the continuous training objective in Eq. (7), and increasing the network depth, we can further improve sample quality for all models. The resulting architectures are denoted as NCSN++ cont. and DDPM++ cont. in Table 3 for VE and VP/sub-VP SDEs respectively. Results reported in Table 3 are for the checkpoint with the smallest FID over the course of training, where samples are generated with PC samplers. In contrast, FID scores and NLL values in Table 2 are reported for the last training checkpoint, and samples are obtained with black-box ODE solvers. As shown in Table 3, VE SDEs typically provide better sample quality than VP/sub-VP SDEs, but we also empirically observe that their likelihoods are worse than VP/sub-VP SDE counterparts. This indicates that practitioners likely need to experiment with different SDEs for varying domains and architectures.
Our best model for sample quality, NCSN++ cont. (deep, VE), doubles the network depth and sets new records for both inception score and FID on unconditional generation for CIFAR-10. Surprisingly, we can achieve better FID than the previous best conditional generative model without requiring labeled data. With all improvements together, we also obtain the first set of high-fidelity samples on CelebA-HQ 1024 × 1024 from score-based models (see Appendix H.3). Our best model for likelihoods, DDPM++ cont. (deep, sub-VP), similarly doubles the network depth and achieves a log-likelihood of 2.99 bits/dim with the continuous objective in Eq. (7). To our best knowledge, this is the highest likelihood on uniformly dequantized CIFAR-10.
5. Controllable Generation



6. Conclusion
We presented a framework for score-based generative modeling based on SDEs. Our work enables a better understanding of existing approaches, new sampling algorithms, exact likelihood computation, uniquely identifiable encoding, latent code manipulation, and brings new conditional generation abilities to the family of score-based generative models.
While our proposed sampling approaches improve results and enable more efficient sampling, they remain slower at sampling than GANs (Goodfellow et al., 2014) on the same datasets. Identifying ways of combining the stable learning of score-based generative models with the fast sampling of implicit models like GANs remains an important research direction. Additionally, the breadth of samplers one can use when given access to score functions introduces a number of hyper-parameters. Future work would benefit from improved methods to automatically select and tune these hyperparameters, as well as more extensive investigation on the merits and limitations of various samplers.
B. VE, VP and Sub-VP SDEs



C. SDEs in the Wild


D. Probability Flow ODE
D.1. Derivation
The idea of probability flow ODE is inspired by Maoutsa et al. (2020), and one can find the derivation of a simplified case therein. Below we provide a derivation for the fully general ODE in Eq. (17). We consider the SDE in Eq. (15), which possesses the following form:


D.2. Likelihood Computation

D.3. Probability Flow Sampling

D.4. Sampling with Black-box ODE Solvers

D.5. Uniquely Identifiable Encoding

E. Reverse Diffusion Sampling

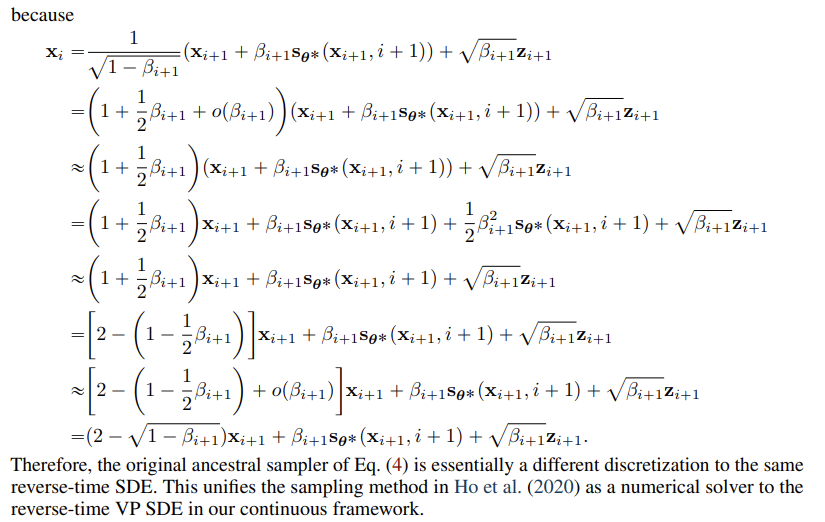
G. Predictor-Corrector Samplers





