Denoising Diffusion Probabilistic Models 정리

Basic Idea of Diffusion Models

Bacis idea of diffusion models is to destroy all the information in the image progressively in a sequence of timestep t where at each step we add a little bit of Gaussian noise and by the end of a large number of steps what we have is a complete random noise mimicking a sample from a normal distribution. 

 

This is called the forward process and we apply this transition function to move from Xt-1 to Xt.

 

We then learn a reverse of this process via a neural network model where effectively what the model is learning is to take the image and remove noise from it step by step and once this model is learned, we can then feed it a random noise sampled from a normal distribution and it will remove little bit of noise from it we then pass this slightly denoised image again and keep repeating this and at the end of a large number of denoising steps we'll get an image from a original distribution 

---

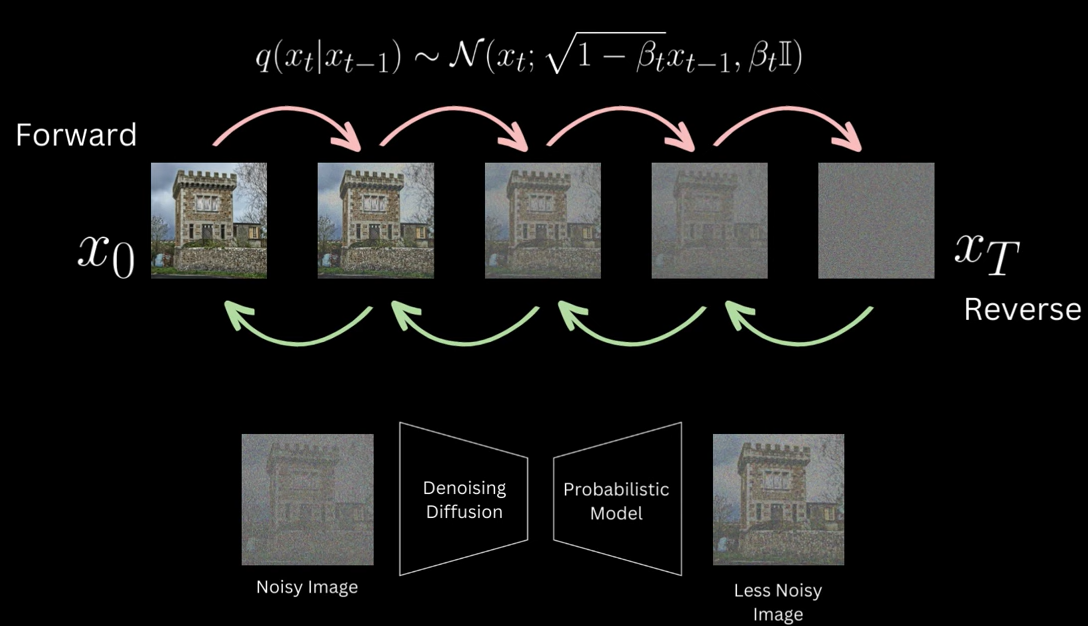
Why call this Diffusion Models

Diffusion: movement of molecules from regions of higher concentration to lower concentraion.

In VAE, we have an image sample and we convert it to a mean and variance of a Gaussian distribution using an encoder and then simultaneously train a decoder that takes a sample from this Gaussian distribution and attepts to reconstruct the image so it seems like we are kind of doing something similar here except not in one shot but through multiple levels. 

 

To answer that once you look more into what diffusion processes are, these are some of the results that you will get.

 

A diffusion process is a stochastic Markov process having continuous sample paths.

 

stochastic : randomness involved
Markov : future state of process will depend only on the present state. once we know the present state, any knowledge about past will give no additional information about the future state.

continous : with no jumps 

 

You can connect this to our equation of forward process where we have this q function which is honoring this Markov definition. Xt is only dependent on Xt-1. 

---

Diffusion is a process of converting samples from a complex distribution to a simple one

 

Our input image distribution is a complex one and if our goal is to convert samples from this distribution to samples from a simple prior that is normal distribution, then this diffusion process can come handy and this mention of repeated application of transition kernel is again referring to this transition function that we have and the claim is that this will lead to a normal distribution.

 

Diffusion is a stochastic Markov process that allows us to transition from any complex distribution to a simple distribution by repeatedly applying a transition kernel.  

---

Transition function in Denoising Diffusion Probabilistic Models - DDPM

Now it seems that the center focus of this diffusion process specifically the forward, where we move from image distribution to normal is this transition function and somehow applying this repeately converts an image which is a sample from a very complex distribution to a sample from a normal distribution.

 

Why is this transition function achieving that effect?

 

What we want to do is gradually shift the distribution to a Gaussian making slow progressive changes. If you really want to model the transition as a diffusion process.

---

Distribution at end of forward Diffusion Process

Transition function ultimately will lead to a mean zero and unit variance Gaussian.

What we did here was discretize the diffusion process into a finite steps for a 1D distribution. 

We can use the same principles to do it for a W x H image and the output for the forward process will then be a W x H image where each pixel is identical to a sample ffrom a Gaussian distribution of mean zero and unit variance.

---

Noise Schedule in Diffusion Models

In practice, we don't use a fixed variance of noise at all steps but se instead use a schedule.

The authors use a linear schedule where they increase the variance of noise over time which makes sense if you think from a reverse process standpoint as when you are at the start of the reverse process, you want the model to learn to make larger jumps and when you are at the end of the reverse process, you're very close to a clear image you want it to make very careful small jumps.

 

Another benefit that I could see is that the schedule actually allows the variance of the distribution to progressively scale very smoothly from the input to the target Gaussian.

---

Recursion to get from original image to noisy image

We are essentially requiring that for t=1000 we have to apply this equation 1000 times to go through the entire Markov chain which is not really efficient.

 

However, it turns out that we don't really need to.

we can actually go from the initial image to the noisy version of the image at any time step t in the forward process in one shot.

All we need is this cumulative product term which can be pre-computed. The original image and a noise sample from normal distribution.

All we really did was convert image to noise and you would agree there are simpler ways to do that so why go through all of this how does modeling this forward process benefit us if ultimately all we did was convert it to noise.

It turns out that under certain conditions which are met here the reverse process is also a diffusion process with transitions having the same functional form which then means that our reverse process which is actually generating data from random noise will also be a markov chain with Gaussian transition probability. 

But we can't straightly compute it because that would require computations involving the entire data distribution however we can approximate it by a distribution P which is formulated as a Gaussian whose mean and sigma are the parameters that we are interested in learning. 

This formalation can be done because we know that the reverse will have that form according to the theory.

---

VAriational Lower Bound in Denoising Diffusion Probabilistic Models - DDPM

We want to learn p(x|z) such that se are able to generate images as close to our training data distribution as possible.

And for that we try to maximize the log likelihood of the observed data. 

So we have log p(x) and we can rewrite it as marginalizing over the latent variables.

We can get the lower bound of the log likelihood of our data, and instead of maximizing the likelihood we can maximize this lower bound.

Instead of going to Z_T in one go, we move through a sequence of latent X1 to XT.

 

So again we want to maximize the likelihood of the observed data which is log p(x0). This is equivalent to integrating out everything from x1 to xT from the joint distribution of the entire chain and applying our inequality for concave functions, we get this, which is our lower bound that we'll maximize which is kind of what we got in the VAE case as well.

 

But up until now we haven't really use the fact that both forward and reverse are Morkov chains.

---

Remember all of this was under the expectation of q.

Now this is very similar to the VAE lower bound.

=>

(1) KL divergence prior term (q is fixed and the final q of X_T will very close to Normal distribution so this is parameter free and we won't bother optimizing this)

(2) + reconstruction of input x0 given x1

(3) + sum of KL divergence

 

=> Require approximate denoising transition distribution to be close to the ground truth denoising transition distribution conditioned on x0.

---

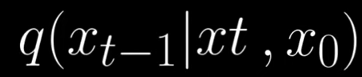
Instead of q(x_t-1|x_t), we have additional conditioning on x0 and intuitively this is something that's easier to compute because once you look at the original image, you can have some sense as to how to go about denoising this image from one time step to previous time step.

In fact, we'll compute this quantity next and we'll see that it has a very nice form.

These were our likelihood terms that we had to optimize and for the last term, we need to compute q(x_t-1|x_t, x0) which we have done. 

 

If you take a closer look at the mean, then it's kind of a weighted average of X_t and x0.

 

And if you compute this weight for x0, then you will see that it is a very low value at higher time steps and as we move closer to the end of the reverse process, this weight increases.

 

Weight for x0 is just zero for a long time but when you actually plot the log values you can see that there's indeed an increase over time 

 

 

This is what we need to compute.

We obviously have to approximate it because for generation, we won't really have x0.

But because we know that our reverse is a Gaussian, we can have our approximation also as a Gaussian.

and all we need to do is learn the mean and variance.

 

The first thing that the authors do is fix the variance to be exactly same as the ground truth denoising step variance.

 

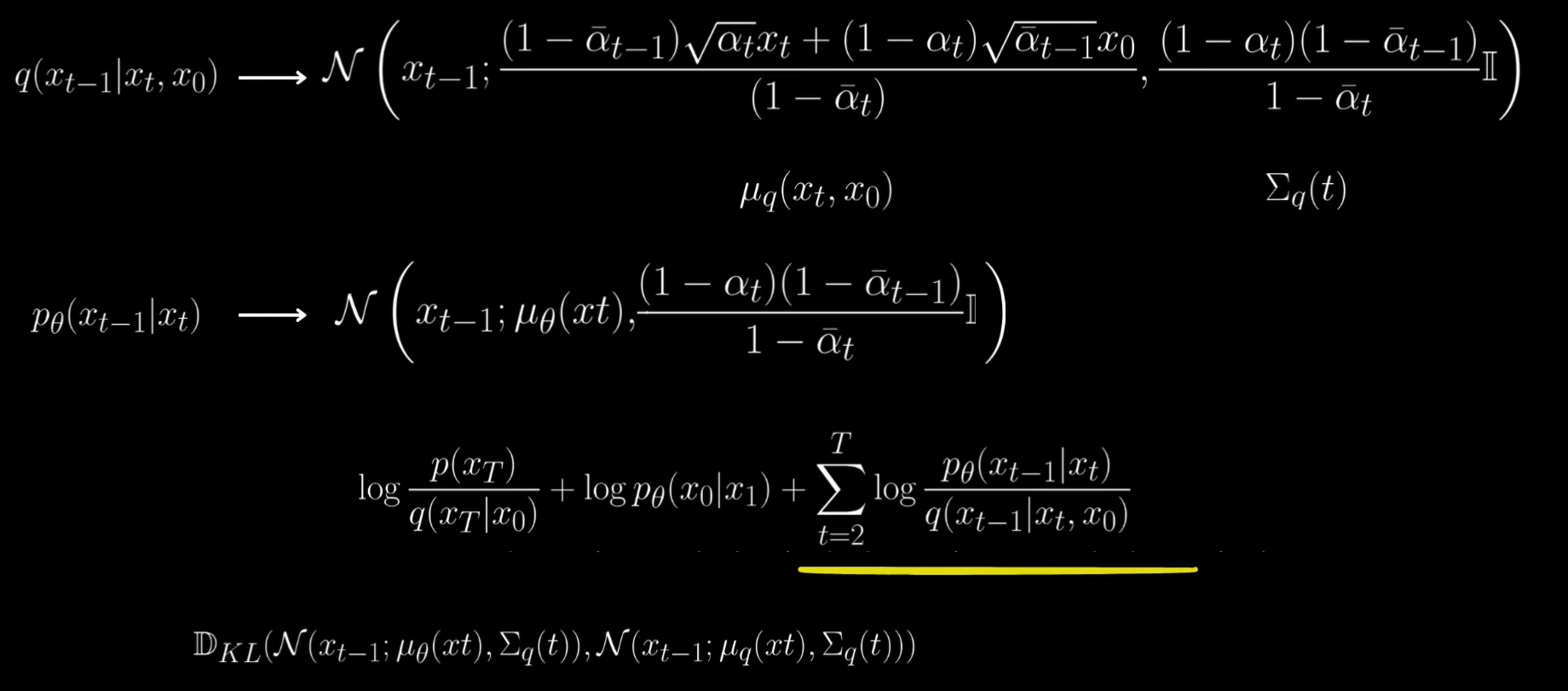
Since our goal is to maximize the likelihood, we need to reduce this difference.

Because our ground truth denoising step has mean in this form (mu_theta), we can rewrite the mean for our approximate denoising distribution also in this form.

 

However, we don't have x0, we'll approximate it by X_theta. 

 

So at any timestep t, x_theta will be our approximation of the original image based on what x_t looks like.

Loss term: how well our model approximates the original image seeing a noisy image at timestep t. 

---

Loss as Noise Prediction

Authors actually formulate loss as how well our model aproximates the noise that was used which can actually be derived from what we have here.

Now our mean differnces will become square difference of the ground truth noise and the predicted noise.

 

Recap

From our likelihood terms, ignored the first one because it did not have any trainable parameters, upon working on the individual terms in the last summation, we identified that it can be written as acaled square difference between the ground truth noise and the noise prediction generated by some model using xt as input.

 

In practice, we also provide timestep as well to the model but that is something we'll anyway cover in the implementation. 

 

Authors actually ignore the scaling altogether and through experiments, find that just training a model on the square difference of noise is good enough.

 

Even the second term in likelihood is also wrapped under this loss by having the model approximate the noise that was added to x0 to get to x1.

During training, t = 1 is treated as same as any timestep and the only minor difference happens is sampling which we'll see soon. 

---

Training of DDPM

During training we'll sample an image from our dataset and also sample a timestep t uniformly. 

The we sample a random noise from a normal distribution.

 

We use the below formulation to get the noisy version of this image in the diffusion process at timestep t. 

 

The original image and sampled noise are used and we use the timestep and our noise schedule to get the cumulative product terms which we can also pre-compute.

 

The noisy version of this image is then fed to our neural network and we train the network using the Loss to ensure that the predicted noise is as close to actual nolise as possible.

 

Training for a large number of steps, we'll cover all the timesteps, and effectively we are optimizing each individual member of this sum term. 

---

Sampling in DDPM

for image generation, we need to go through the reverse process and we can do that by iteratively sampling through our approximation of the denoising step distribution p that our neural network has learned. 

 

For generating, we start with a random sample from a normal distribution as our final step T image. We pass it to our trained model to get the predicted noise and just reiterate our approximate denoising distribution.

 

We formulated the mean this way using noisy image at timestep t, and predicted noise. 

 

If you simplify the terms, you end up with the mean image of the denoising distribution as this.

 

Once we have the predicted noise, we can sample an image from this distribution using the mean image and the variance which was actually fixed to be same as the forward process and this becomes our X_t-1.

Then we just keep on repeating this process all the way until we get our original image x0.

 

The only thing we do differently is we return the mean image itself to get from x1 to x0.