Why Does Contrastive Learning Work?

* Contrastive learning은 왜 good representation을 학습하도록 하는가?

* 그럼 good representation이란 건 뭔가?

* Contrastive learning이 성공하기 위한 조건은 무엇인가?

 

이 궁금증에 대하여 이론적 증명을 보인 논문 2편을 가져왔다.

 

중간 단계의 수식은 이해하기 어려워서 적당히 넘겼지만, contrastive learning이 어떻게 작동하는지 (loss function이 어떻게 feature representation을 feature space 상에 놓이게 하는지) 를 어느정도 이해한 것 같다.

 

Contrastive learning이 성공하기 위해서는 large batch size, augmentation method, hard negative가 중요한 요소.

 

다만 논문에서 제시한 이론 상으로는 batch size가 클수록 good representation을 학습한다고 하는데,

SigLip 논문에서 보여준 empirical results는 softmax와 sigmoide loss 모두 32k에서 saturate된다고 한다.

 

이 gap은 이론적 증명에서의 assumption과 현실과의 gap에서 온건가..?

 

* 추가적으로 궁금한 거

- negative sample 없는 방법을 제시한 연구: e.g. BYOL

- 어떨 때 contrastive learning이 제대로 작동하지 못하는가 (dimension collapse) → 그럴 때 어떻게 해결하는가

---

1. Understanding Contrastive Representation Learning through Alignment and Uniformity on the Hypersphere

https://arxiv.org/pdf/2005.10242

 

 

In this paper, the authors examine the properties of self-supervised data representations trained via a contrastive learning procedure. The paper demonstrated that data representations (features) derived through the contrastive learning objective have two following properties:

1. Alignment (closeness) between features of positive pairs of examples
2. Uniformity (uniform distribution) of the data representation on the unit hypersphere (see the remark below). Intuitively, uniformity of feature distribution indicates that the data representations retain maximal information from the original data.

The main result of the paper states that the contrastive learning objective directly optimizes both aforementioned properties when the number of negative samples reaches infinity. Simply put, when the number of negative examples in a batch is high, optimizing the contrastive loss objective leads to aligned and uniformly distributed data representations.

 

It is known that increasing the number of negative examples in contrastive learning methods usually results in better data representations. From this perspective, replacing a contrastive learning objective with a combined uniformity and alignment objective may be able to extract more powerful data features. To impose uniformity and alignment properties on data representations, the authors introduced theoretically-anchored metrics to measure their (representations’) alignment and uniformity. Finally, the paper showed that incorporating these metrics into the representation learning objective together with the contrastive loss, produced better data features.

---

Let’s try to provide some insight into why alignment and uniformity can be natural properties of data representation, derived through the contrastive loss objective. We start with the following (the most widely used) form of contrastive loss:

 

Assuming positive examples have the same representation/are perfectly aligned (with a dot product equal to 1, since they both have a unit norm) the above expression becomes:

 

 

When the number of negative examples M is very large, the minimum of the last expression is attained when pairwise distances between data representations are maximal (dot product at the exponent is as close to zero as possible). So alignment and uniformity appear to be natural properties of good data representation (attains small value of the contrastive loss).

 

---

2. Provable Guarantees for Self-Supervised Deep Learning with Spectral Contrastive Loss

https://arxiv.org/pdf/2106.04156

Augmentation graph for self-supervised learning

The key idea behind our work is the idea of a population augmentation graph. This graph is built such that the nodes represent all possible augmentations of all data points in the population distribution and the edges connect nodes that are derived from the same natural image. Further, the edges are weighted to be the probability that the two augmented images are augmentations of the same underlying image, given the set of augmentation functions being used. Some augmentation methods, like cropping, produce images that could only come from the same underlying image. However, others, such as Gaussian blurring, technically connect all images to each other, albeit mostly with very small probabilities. The figure below gives a visualization of the graph, where augmented images of French bulldogs are connected in the graph.

 

We have two simple intuitions about the graph that suggests it contains information generally useful for a pre-trained computer vision model. First, very few high-probability edges exist between any two images, especially if they have different semantic content. For instance, consider two pictures of the same dogs in different poses. Even though the semantic content is the same, there is almost zero chance that one could produce one image from the other using augmentation methods like Gaussian blur. This probability is reduced further when considering two images that don’t even share the same objects, such as one image of a dog outside and another image of a cruise ship in the ocean. Rather, the only high-probability connections are augmented images with similar objects in similar orientations or poses.

 

Second, images with similar content (e.g, dog images of the same breed) can be connected to each other via a path of interpolating images. The figure above visualizes this intuition, where x1 and x2 are two augmented images of French bulldogs that aren’t obtained from the same natural image (hence no high-probability edge between them). However, since the augmentation graph is a theoretical construct that is defined on the population data which contains all possible dog images, there must exist a path of interpolating French bulldog images (as shown in Figure 1) where every consecutive two images are directly connected by a reasonably high-probability edge. As a result, this sequence forms a path connecting x1 and x2.

---

Graph partitioning via spectral decomposition

Consider an ideal world where we can partition the augmentation graph into multiple disconnected subgraphs. From the intuition above, each subgraph contains images that can be easily interpolated into each other, and so likely depicts the same underlying concept or objects in its images. This motivates us to design self-supervised algorithms that can map nodes within the same subgraph to similar representations.

 

Assume we have access to the population data distribution and hence the whole augmentation graph. A successful algorithm for graph partitioning is spectral clustering (Shi & Malik 2000, Ng et al. 2002), which uses spectral graph theory tools to discover the connected components in a graph. We’ll interpret contrastive learning as an effective, parametric way to implement spectral clustering on the large augmentation graph. 

---

Contrastive learning as spectral clustering

We can use these intuitions about spectral clustering to design a contrastive learning algorithm. Specifically, because we don’t have access to the true population augmentation graph, we instead define fθ which is a neural network that takes in an example and outputs the eigenvector representation of the example. Put another way, our goal is to compute the matrix F that contains the eigenvectors as columns, and use its rows as the representations. We aim to learn fθ such that fθ(x) is the row of matrix F corresponding to example x. Given the high expressivity of neural nets, we assume that such a θ exists.

 

It turns out that this feature can be learned by minimizing the following “matrix factorization loss”:

 

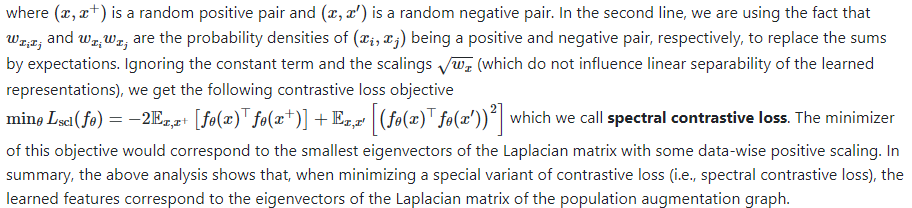
Empirically, features learned by training spectral contrastive loss can match strong baselines such as SimCLR and SimSiam. The above table shows the linear probe accuracy with 100-epoch pre-training on ImageNet. 

---

Why does this method produce good representations?

We now turn to the question we began with: why are the representations learned by contrastive loss useful for downstream computer vision tasks? We study the downstream accuracy of the representation with the “linear probe” protocol (Chen et al. 2020), where an additional linear model is trained on the representation to predict the labels for a downstream classification task. As discussed above, the representations learned by the spectral contrastive loss are the rows (with data-wise positive scaling) of a matrix where the columns are the smallest eigenvectors of the Laplacian matrix. Since the scaling doesn’t change the linear prediction, it suffices to consider the rows of the eigenvector matrix as representations. The usefulness of this representation in classification tasks can be demonstrated by the following didactic example: consider a augmentation graph G with three completely disconnected components that correspond to three classes, and the downstream task is to classify one component (e.g., set {x1,x2,x3} versus the rest).

The figure above shows the smallest eigenvectors of the Laplacian, where the blank entries are 0. It’s easy to see that here rows of the eigenvector matrix exactly correspond to indicators of different components in the graph, and hence the representations of nodes from different connected subgraphs are clearly linearly separable. For instance, if we use the sign of f(x)⊤b as the predictor where vector b∈Rk is set to be e1, we can perfectly classify whether a node belongs to set {x1,x2,x3} or not. The same intuition holds in a broader setting where the graph isn’t regular, the components aren’t necessarily disconnected, and the downstream task has more than two classes. In summary, the contrastive learned representation can linearly predict any set of nearly disconnected components with high accuracy, which is captured by the following theorem: 

 

Theorem (informal): Assume the population augmentation graph contains k approximately disconnected components, where each component corresponds to a downstream class. Let the feature map f:X→Rk be the minimizer of the population spectral contrastive loss. Then, there exists a linear head on top of f that achieves small downstream classification error. 

---

Conclusion

Our theory suggests that self-supervised learning can learn quite powerful and diverse features that are suitable for a large set of downstream tasks. To see this, consider a situation where there are a large number of disconnected subgraphs in the augmentation graph, the downstream task can be an arbitrary way of grouping these subgraphs into a small number of classes (each class can correspond to many subgraphs, .e.g., the “dog” class may contain many subgraphs corresponding to different breeds of dogs). 

---

References

https://www.keep-current.com/understanding-contrastive-representation-learning-through-alignment-and-uniformity-on-the-hypersphere

https://ai.stanford.edu/blog/understanding-contrastive-learning/