[Time-MoE] Billion-Scale Time Series Foundation Models with Mixture of Experts

https://arxiv.org/pdf/2409.16040

https://github.com/Time-MoE/Time-MoE

(Sep 2024)

---

Abstract

Deep learning for time series forecasting has seen significant advancements over the past decades. However, despite the success of large-scale pre-training in language and vision domains, pre-trained time series models remain limited in scale and operate at a high cost, hindering the development of larger capable forecasting models in real-world applications. In response, we introduce TIME-MOE, a scalable and unified architecture designed to pre-train larger, more capable forecasting foundation models while reducing inference costs. By leveraging a sparse mixture-of-experts (MoE) design, TIME-MOE enhances computational efficiency by activating only a subset of networks for each prediction, reducing computational load while maintaining high model capacity. This allows TIME-MOE to scale effectively without a corresponding increase in inference costs. TIME-MOE comprises a family of decoder-only transformer models that operate in an autoregressive manner and support flexible forecasting horizons with varying input context lengths. We pre-trained these models on our newly introduced large-scale data Time-300B, which spans over 9 domains and encompassing over 300 billion time points. For the first time, we scaled a time series foundation model up to 2.4 billion parameters, achieving significantly improved forecasting precision. Our results validate the applicability of scaling laws for training tokens and model size in the context of time series forecasting. Compared to dense models with the same number of activated parameters or equivalent computation budgets, our models consistently outperform them by large margin. These advancements position TIME-MOE as a state-of-the-art solution for tackling real-world time series forecasting challenges with superior capability, efficiency, and flexibility.

---

1. Introduction

Time series data is a major modality in real-world dynamic systems and applications across various domains (Box et al., 2015; Zhang et al., 2024; Liang et al., 2024). Analyzing time series data is challenging due to its inherent complexity and distribution shifts, yet it is crucial for unlocking insights that enhance predictive analytics and decision-making. As a key task in high demand, time series forecasting has long been studied and is vital for driving various use cases in fields such as energy, climate, education, quantitative finance, and urban computing (Jin et al., 2023; Nie et al., 2024; Mao et al., 2024). Traditionally, forecasting has been performed in a task-specific, end-to-end manner using either statistical or deep learning models. Despite their competitive performance, the field has not converged on building unified, general-purpose forecasting models until recently, with the emergence of a few foundation models (FMs) for universal forecasting (Das et al., 2024; Woo et al., 2024; Ansari et al., 2024). Although promising, they are generally small in scale and have limited task-solving capabilities compared to domain-specific models, limiting their real-world impact when balancing forecasting precision against computational budget.

 

Increasing model size and training tokens typically leads to performance improvements, as known as scaling laws, which have been extensively explored in the language and vision domains (Kaplan et al., 2020; Alabdulmohsin et al., 2022). However, such properties have not been thoroughly investigated in the time series domain. Assuming that scaling forecasting models with high-quality training data follows similar principles, several challenges remain: Dense versus sparse training. Most time series forecasting models compose of dense layers, which means each input time series tokens requires computations with all model parameters. While effective, this is computationally intensive. In contrast, sparse training with mixture-of-experts (MoE) is more flop-efficient per parameter and allows for scaling up model size with a fixed inference budget while giving better performance, as showcased on the right of Figure 1. However, optimizing a sparse, large-scale time series model faces another challenge of stability and convergency. Time series are highly heterogeneous (Woo et al., 2024; Dong et al., 2024), and selecting the appropriate model design and routing algorithm often involves a trade-off between performance and computational efficiency. Sparse solutions for time series foundation models have yet to be explored, leaving a significant gap in addressing these two challenges. While time series pre-training datasets are no longer a major bottleneck, most existing works (Das et al., 2024; Woo et al., 2024; Ansari et al., 2024) have not extensively discussed their in-model data processing pipelines or mixing strategies. Answering this is particularly important, given that existing data archives are often noisy and largely imbalanced across domains.

 

On the other hand, most time series FMs face limitations in flexibility and generalizability. General-purpose forecasting is a fundamental capability, requiring a model to handle any forecasting problems, regardless of context lengths, forecasting horizons, input variables, and other properties such as frequencies and distributions. Meanwhile, achieving strong generalizability pushes the boundaries further that existing works often fail to meet simultaneously. For instance, Timer (Liu et al., 2024b) has limited native support for arbitrary output lengths, which may lead to truncated outputs, while Moment (Goswami et al., 2024) operates with a fixed input context length. Although Moirai (Woo et al., 2024) achieves universal forecasting, it depends on hardcoded heuristics in both the input and output layers.

 

The recognition of the above challenges naturally raises a pivotal question:

 

Answering this question drives the design of TIME-MOE, a scalable and unified architecture for pre-training larger, more capable forecasting FMs while reducing computational costs. TIME-MOE consists of a family of decoder-only transformer models with a mixture-of-experts architecture, operating in an auto-regressive manner to support any forecasting horizon and accommodate context lengths of up to 4096. With its sparsely activated design, TIME-MOE enhances computational efficiency by activating only a subset of networks for each prediction, reducing computational load while maintaining high model capacity. This allows TIME-MOE to scale effectively without significantly increasing inference costs. Our proposal is built on a minimalist design, where the input time series is point-wise tokenized and encoded before being processed by a sparse transformer decoder, activating only a small subset of parameters. Pre-trained on large-scale time series data across 9 domains and over 300 billion time points, TIME-MOE is optimized through multi-task learning to forecast at multiple resolutions. During inference, different forecasting heads are utilized to enable forecasts across diverse scales, enabling flexible forecast horizons. For the first time, we scale a time series FM up to 2.4 billion parameters, achieving substantial improvements in forecasting precision compared to existing models, as shown on the left of Figure 1. Compared to dense models with the same number of activated parameters or equivalent computational budgets, our models consistently outperform them by a large margin. Our contributions lie in three aspects:

 

1. We present TIME-MOE, a universal decoder-only time series forecasting foundation model architecture with mixture-of-experts. To the best of our knowledge, this is the first work to scale time series foundation models up to 2.4 billion parameters. TIME-MOE achieves substantial improvements in forecasting accuracy and consistently outperforms dense models with comparable computational resources, while maintaining high efficiency.

 

2. We introduce Time-300B, the largest open-access time series data collection, comprising over 300 billion time points spanning more than nine domains, accompanied by a well-designed data-cleaning pipeline. Our TIME-MOE models and Time-300B data collection are open-sourced.

 

3. Trained on Time-300B, TIME-MOE models outperform other time series foundation models with a similar number of activated parameters across six real-world benchmarks, achieving reductions in forecasting errors by an average of 20% and 24% in zero-shot and in-distribution scenarios, respectively.

---

2. Related Work

Time Series Forecasting.

Deep learning models have become powerful tools for time series forecasting over the past decade, which can be broadly categorized into two types: (1) univariate models, such as DeepState (Rangapuram et al., 2018), DeepAR (Salinas et al., 2020), and N-BEATS (Oreshkin et al., 2020), which focus on modeling individual time series, and (2) multivariate models, which include both transformer-based approaches (Wen et al., 2023; Zhou et al., 2021; Nie et al., 2023; Liu et al., 2024a; Wang et al., 2024c; Chen et al., 2024) and non-transformer models (Sen et al., 2019; Jin et al., 2022; Wang et al., 2024b; Hu et al., 2024; Qi et al., 2024), designed to handle multiple time series simultaneously. While these models achieve competitive in-domain performance, many are task-specific and fall short in generalizability when applied to cross-domain data in few-shot or zero-shot scenarios.

Large Time Series Models.

Pre-training on large-scale sequence data has significantly advanced modality understanding in language and vision domains (Dong et al., 2019; Selva et al., 2023). Building on this progress, self-supervised learning has been extensively developed for time series (Zhang et al., 2024), employing masked reconstruction (Zerveas et al., 2021; Nie et al., 2023) or contrastive learning (Zhang et al., 2022; Yue et al., 2022; Yang et al., 2023). However, these methods are limited in both data and model scale, with many focused on in-domain learning and transfer. Recently, general pre-training of time series models on large-scale data has emerged, though still in its early stages with insufficient exploration into sparse solutions. We discuss the development more in Appendix A. Unlike these dense models, TIME-MOE introduces a scalable and unified architecture for pre-training larger forecasting foundation models, which is also more capable while maintaining the same scale of activated parameters or computational budget as dense models.

Sparse Deep Learning for Time Series.

Deep learning models are often dense and over-parameterized (Hoefler et al., 2021), leading to increased memory and computational demands during both training and inference. However, sparse networks, such as mixture-of-experts models (Jacobs et al., 1991), which dynamically route inputs to specialized expert networks, have shown comparable or even superior generalization to dense models while being more efficient (Fedus et al., 2022; Riquelme et al., 2021). In time series research, model sparsification has received less attention, as time series models have traditionally been small in scale, with simple models like DLinear (Zeng et al., 2023) and SparseTSF (Lin et al., 2024) excelling in specific tasks prior to the advent of large-scale, general pre-training. The most relevant works on this topic include Pathformer (Chen et al., 2024), MoLE (Ni et al., 2024), and IME (Ismail et al., 2023). However, none of them delve into the scalability of foundation models with sparse structures. Besides, MoLE and IME are not sparse models, as input data is passed to all heads and then combined to make predictions.

---

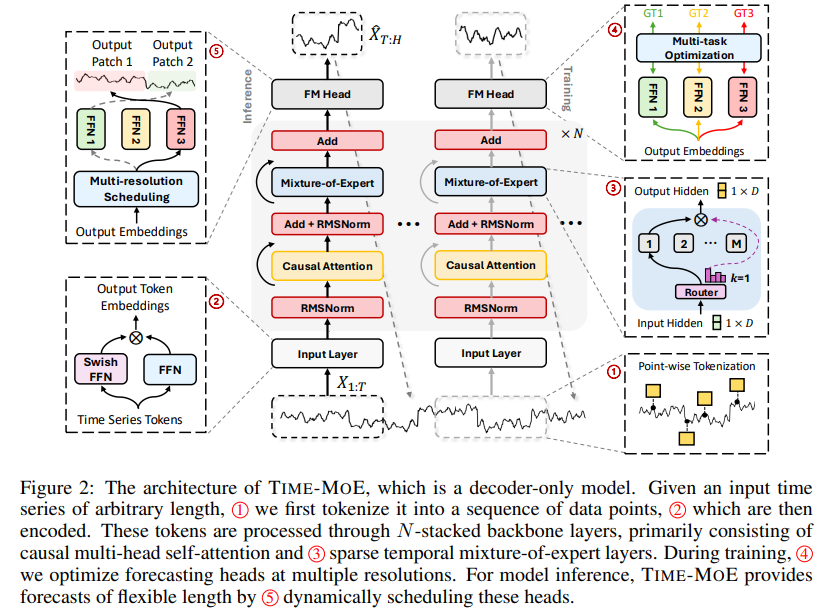
3. Methodology

Our proposed TIME-MOE, illustrated in Figure 2, adopts a mixture-of-experts-based, decoder-only transformer architecture, comprising three key components: (1) input token embedding, (2) MoE transformer block, and (3) multi-resolution forecasting. For the first time, we scale a sparsely-activated time series model to 2.4 billion parameters, achieving significantly better zero-shot performance with the same computation. This marks a major step forward in developing large time series models for universal forecasting.

Problem Statement.

We address the problem of predicting future values in a time series: given a sequence of historical observations X1:T = (x1, x2, . . . , xT ) ∈ R T spanning T time steps, our objective is to forecast the next H time steps, i.e., Xˆ T +1:T +H = fθ (X1:T ) ∈ R H. Here, fθ represents a time series model, where T is the context length and H is the forecasting horizon. Notably, both T and H can be flexible during TIME-MOE inference, distinguishing it from task-specific models with fixed horizons. Additionally, channel independence (Nie et al., 2023) is adopted to transform a multivariate input into univariate series, allowing TIME-MOE to handle any-variate forecasting problems in real-world applications.

---

3.1. Time-MoE Overview

Input Token Embedding.

We utilize point-wise tokenization for time series embedding to ensure the completeness of temporal information. This enhances our model’s flexibility and broad applicability in handling variable-length sequences. Then, we employ SwiGLU (Shazeer, 2020) to embed each time series point:

where W ∈ RD×1 and V ∈ RD×1 are learnable parameters, and D denotes the hidden dimension.

MoE Transformer Block.

Our approach builds upon a decoder-only transformer (Vaswani, 2017) and integrates recent advancements from large language models (Bai et al., 2023; Touvron et al., 2023). We employ RMSNorm (Zhang & Sennrich, 2019) to normalize the input of each transformer sub-layer, thereby enhancing training stability. Instead of using absolute positional encoding, we adopt rotary positional embeddings (Su et al., 2024), which provide greater flexibility in sequence length and improved extrapolation capabilities. In line with (Chowdhery et al., 2023), we remove biases from most layers but retain them in the QKV layer of self-attention to improve extrapolation. To introduce sparsity, we replace a feed-forward network (FFN) with a mixture-of-experts layer, incorporating a shared pool of experts that are sparsely activated.

 

Here, SA denotes self-attention with a causal mask, and Mixture refers to the mixture-of-experts layer. In practice, Mixture comprises several expert networks, each mirroring the architecture of a standard FFN. An individual time series point can be routed to either a single expert (Fedus et al., 2022) or multiple experts (Lepikhin et al., 2020). One expert is designated as a shared expert to capture and consolidate common knowledge across different contexts.

Multi-resolution Forecasting.

We introduce a novel multi-resolution forecasting head, which allows for forecasting at multiple scales simultaneously, in contrast to existing foundation models that are limited to a single fixed scale. This capability enhances TIME-MOE ’s flexibility by enabling forecasting across various horizons. The model employs multiple output projections from single-layer FFNs, each designed for different prediction horizons. During training, TIME-MOE aggregates forecasting errors from different horizons to compute a composite loss (Section 3.2.2), thereby improving the model generalization. By incorporating a simple greedy scheduling algorithm (see Appendix B), TIME-MOE efficiently handles predictions across arbitrary horizons. This design also boosts prediction robustness through multi-resolution ensemble learning during inference.

---

3.2. Model Training

3.2.1. Time-300B Dataset

Training time series foundation models require extensive, high-quality data. However, well-processed large-scale datasets are still relatively scarce. Recent advancements have facilitated the collection of numerous time series datasets from various sources (Godahewa et al., 2021; Ansari et al., 2024; Woo et al., 2024; Liu et al., 2024b). Nonetheless, data quality still remains a challenge, with prevalent issues such as missing values and invalid observations (Wang et al., 2024a) that can impair model performance and destabilize training. To mitigate these issues, we developed a streamlined data-cleaning pipeline (Appendix C) to filter and refine raw data, and constructed the largest open-access, high-quality time series data collection named Time-300B for foundation model pre-training. Time-300B is composed of a diverse range of publicly available datasets, spanning multiple domains such as energy, retail, healthcare, weather, finance, transportation, and web, as well as a portion of synthetic data to enhance the data quantity and diversity. Time-300B covers a wide spectrum of sampling frequencies from seconds to yearly intervals, and has over 300 billion time points after being processed by our data-cleaning pipeline, as summarized in Table 1.

---

3.2.2. Loss Function

Pre-training time series foundation models in large scale presents significant challenges in training stability due to the massive datasets and the vast number of parameters involved. To address this, we use the Huber loss (Huber, 1992; Wen et al., 2019), which provides greater robustness to outliers and improves training stability:

 

When training the model with a MoE architecture, focusing solely on optimizing prediction error often leads to load imbalance issues among the experts. A common problem is routing collapse (Shazeer et al., 2017), where the model predominantly selects only a few experts, limiting training opportunities for others. To mitigate this, following the approaches of (Dai et al., 2024; Fedus et al., 2022), we achieve expert-level balancing with an auxiliary loss to reduce routing collapse:

---

3.2.3. Model Configurations and Training Details

 

Informed by the scaling laws demonstrated by Llama (Dubey et al., 2024; Touvron et al., 2023), which show that a 7- or 8-billion parameter model continues to improve performance even after training on over one trillion tokens, we chose to scale TIME-MOE up to 2.4 billion parameters with around 1 billion of them activated. This model, TIME-MOE_ultra, supports inference on consumer-grade GPUs with less than 8GB of VRAM. We have also developed two smaller models: TIMEMOE_base, with 50 million activated parameters, and TIME-MOE_large, with 200 million activated parameters, both specifically designed for fast inference on CPU architectures. These streamlined models are strategically developed to ensure broader accessibility and applicability in resource-constrained environments. The detailed model configurations are in Table 2. Each model undergoes training for 100, 000 steps with a batch size of 1024, where the maximum sequence length is capped at 4096. This setup results in the consumption of 4 million time points per iteration. We choose {1, 8, 32, 64} as different forecast horizons in the output projection and set the factor of the auxiliary loss α to 0.02. For optimization, we employ the AdamW optimizer, configured with the following hyperparameters: lr = 1e-3, weight decay = 0.1, β1 = 0.9, β2 = 0.95. A learning rate scheduler with a linear warmup over the initial 10, 000 steps followed by cosine annealing is also utilized. Training is conducted on 128 × NVIDIA A100-80G GPUs using BF16 precision.

---

4. Main Results

TIME-MOE consistently outperforms state-of-the-art forecasting models by large margins across six well-established benchmarks and settings (Appendix B). To ensure a fair comparison, we adhered to the experimental configurations from (Woo et al., 2024) for out-of-distribution forecasting and (Wu et al., 2023a) for in-distribution forecasting with a unified evaluation pipeline we developed. Specifically, we evaluate TIME-MOE against 16 different baselines, representing state-of-the-art models in long-term forecasting. They are categorized into two groups: 1. zero-shot forecasting evaluation group, includes pre-trained foundation models such as Moirai (2024), TimesFM (2024), Moment (2024), and Chronos (2024); 2. in-distribution (full-shot) forecasting evaluation group, consists of modern time series models such as iTransformer (2024a), TimeMixer (2024b), TimesNet (2023a), PatchTST (2023), Crossformer (2023), TiDE (2023), DLinear (2023), and FEDformer (2022b).

---

4.1. Zero-shot Forecasting

Setup.

Time series foundation models have recently demonstrated impressive zero-shot learning capabilities (Liang et al., 2024). In this section, we conducted experiments on the six well-known long-term forecasting benchmarks for which datasets were not included in the pre-training corpora. We use four different prediction horizons, which are {96, 192, 336, 720}, with the corresponding input time series lengths {512, 1024, 2048, 3072}. The evaluation metrics adopt mean square error (MSE) and mean absolute error (MAE).

Results.

Detailed results of zero-shot forecasting are in Table 3. TIME-MOE achieves consistent state-of-the-art performances, improving a large margin as MSE reduction in average exceeding 20% over the other most competitive baselines. Importantly, as the model size scales (e.g., base → ultra), it continuously exhibits enhanced performance across all datasets, affirming the efficacy of scaling laws within our time series foundation models. Furthermore, in comparisons with robust baselines that have a similar number of activated parameters, TIME-MOE demonstrates significantly superior performance. The largest models among the state-of-the-art baselines are Chronos_large, Moment and Moirai_large. Compared to those models, TIME-MOE achieved average MSE reductions of 23%, 30% and 11% respectively.

---

4.2. In-Distribution Forecasting

Setup.

We fine-tune the pre-trained TIME-MOE models on the train split of the above-mentioned six benchmarks and set the number of finetuning epochs to only one.

Results.

The full results are in Table 4. TIME-MOE exhibits remarkable capabilities, comprehensively surpassing advanced deep time series models from recent years, achieving a MSE reduction of 24% in average. Fine-tuning on downstream data with only one epoch significantly improves predictive performance, showcasing the remarkable potential of large time series models built on the MoE architecture. Similar to zero-shot forecasting, as the model size increases, the scaling law continues to be effective, leading to continuous improvements in the performance of the TIME-MOE.

---

4.3. Ablation Study

Model Architecture.

Replacing the MoE layers with standard FFNs (w/o mixture-of-experts) led to an average performance drop from 0.262 to 0.272, highlighting the performance boost provided by the sparse architecture. A detailed comparison of dense and sparse models is presented in Section 4.4. We retained only the horizon-32 output layer by eliminating the other multi-resolution output layers from the TIME-MOEbase, excluding the multi-task optimization (w/o multi-resolution layer). Consequently, we observed that the performance of this modified model was slightly inferior compared to that of the TIME-MOEbase. Additionally, as shown in the right side of Table 5, our default selection of four multi-resolution output projections with receptive horizons of {1, 8, 32, 64} results in optimal predictive performance and inference speed. As we reduce the number of multi-resolution output projections, performance consistently declines, and inference speed significantly increases. This demonstrates the rationality of our multi-resolution output projection design.

Training Loss.

Models trained with Huber loss outperformed those using MSE loss (w/o Huber loss), due to Huber loss’s superior robustness in handling outlier time points. We also removed the auxiliary loss from the objective function, retaining only the auto-regressive loss (w/o auxiliary loss) while still using the MoE architecture. This adjustment caused the expert layers to collapse into a smaller FFN during training, as the activation score of the most effective expert became disproportionately stronger without the load balance loss. Consequently, the model’s performance was significantly worse than the TIME-MOEbase.

---

4.4. Scalability Analysis

Dense versus Sparse Models.

To assess the performance and efficiency benefits of sparse architectures in time series forecasting, we replaced the MoE layer with a dense layer containing an equivalent number of parameters as the activated parameters in the MoE layer. Using identical training setup and data, we trained three dense models corresponding to the sizes of the three TIMEMOE models. A zero-shot performance comparison between the dense and sparse models is shown in Figure 3. Our approach reduced training costs by an average of 78% and inference costs by 39% compared to dense variants. This clearly demonstrates the advantages of TIME-MOE, particularly in maintaining exceptional performance while significantly reducing costs.

Model and Data Scaling.

We save model checkpoints at intervals of every 20 billion time points during training, allowing us to plot performance traces for models of different sizes trained on various data scales. The right side of Figure 3 shows that models trained on larger datasets consistently outperform those trained on smaller datasets, regardless of model size. Our empirical results confirm that as both data volume and model parameters scale, sparse models demonstrate continuous and substantial improvements in performance, as well as achieve better forecasting accuracy compared to the dense counterparts under the same scales.

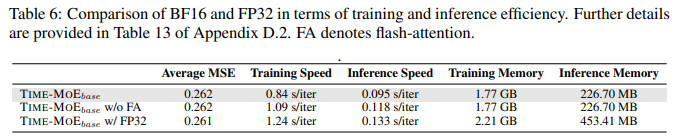
Training Precision.

We trained a new model, TIME-MOE_base (FP32), using identical configurations but with float32 precision instead of bfloat16. As shown in Table 6, the forecasting performance of both models is comparable. However, the bfloat16 model achieves a 12% improvement in training speed and reduces memory consumption by 20% compared to the float32 model. Moreover, the bfloat16 model can seamlessly integrate with flash-attention (Dao, 2024), further boosting training and inference speed by 23% and 19% respectively.

---

4.5. Sparsification Analysis

Activation Visualization.

As shown in Figure 4, TIME-MOE dynamically activates different experts across various datasets, with each expert specializing in learning distinct knowledge. This leads to diverse activation patterns across datasets from different domains, showcasing TIME-MOE’s strong generalization capabilities. The heterogeneous activations indicate that the model adapts its learned representations to the specific characteristics of each dataset, contributing to its great transferability and generalization as a large-scale time series foundation model.

Number of Experts.

We performed a sensitivity analysis on the number of experts, represented as topk, within the TIME-MOE architecture, as shown in Table 7. As k increases, performance shows only marginal changes, with minimal improvements in average MSE. However, inference time increases noticeably as more experts are utilized. This indicates that increasing sparsity within the MoE architecture does not compromise performance but significantly enhances computational efficiency. This balance is critical for scaling time series foundation models, where optimizing performance and computational cost is essential. Sparse MoE architectures inherently offer advantages in these areas.

---

5. Conclusion

In this paper, we introduced TIME-MOE, a scalable and unified architecture for time series foundation models that leverages a sparse design with mixture-of-experts to enhance computational efficiency without compromising model capacity. Pre-trained on our newly introduced large-scale time series dataset, Time-300B, TIME-MOE was scaled to 2.4 billion parameters, with 1.1 billion activated, demonstrating significant improvements in forecasting accuracy. Our results validate the scaling properties in time series forecasting, showing that TIME-MOE consistently outperforms dense models with equivalent computational budgets across multiple benchmarks. With its ability to perform universal forecasting and superior performance in both zero-shot and fine-tuned scenarios, TIME-MOE establishes itself as a state-of-the-art solution for real-world forecasting challenges. This work paves the way for future advancements in scaling and enhancing the efficiency of time series foundation models.

---

A. Further Related Work

In this section, we delve deeper into the related work on large time series models. Current research efforts in universal forecasting with time series foundation models can be broadly classified into three categories, as summarized in Table 8: (1) encoder-only models, such as Moirai (Woo et al., 2024) and Moment (Goswami et al., 2024), which employ masked reconstruction and have been pre-trained on datasets containing 27B and 1B time points, respectively, with model sizes reaching up to 385M parameters; (2) encoder-decoder models, exemplified by Chronos (Ansari et al., 2024), which offers pre-trained models at four scales, with up to 710M parameters; and (3) decoder-only models, including TimesFM (Das et al., 2024), Lag-Llama (Rasul et al., 2023), and Timer (Liu et al., 2024b), with the largest models containing up to 200M parameters. In contrast to these dense models, TIME-MOE introduces a scalable, unified architecture with a sparse mixture-of-experts design, optimized for larger time series forecasting models while reducing inference costs. Trained on our Time-300B dataset, comprising over 300B time points, TIME-MOE is scaled to 2.4B parameters for the first time. It outperforms existing models with the same number of activated parameters, significantly enhancing both model efficiency and forecasting precision, while avoiding limitations such as fixed context lengths or hardcoded heuristics.

---

B. Implementation Details

Training Configuration.

Each model is trained for 100,000 steps with a batch size of 1,024, and a maximum sequence length capped at 4,096. This setup processes 4 million time points per iteration. We use forecast horizons of {1, 8, 32, 64} in the output projection and set the auxiliary loss factor α to 0.02. For optimization, we apply the AdamW optimizer with the following hyperparameters: lr = 1e-3, weight decay = 1e-1, β1 = 0.9, and β2 = 0.95. A learning rate scheduler with a linear warmup for the first 10,000 steps, followed by cosine annealing, is used. Training is performed on 128 × NVIDIA A100-80G GPUs with BF16 precision. To improve batch processing efficiency and handle varying sequence lengths, we employ sequence packing (Raffel et al., 2020), which reduces padding requirements.

Benchmark Details.

We evaluate the performance of various models for long-term forecasting across eight well-established datasets, including the Weather (Wu et al., 2021), Global Temp (Wu et al., 2023b), and ETT datasets (ETTh1, ETTh2, ETTm1, ETTm2) (Zhou et al., 2021). A detailed description of each dataset is provided in Table 9.

Metrics.

We use mean square error (MSE) and mean absolute error (MAE) as evaluation metrics for time-series forecasting. These metrics are calculated as follows:

where xi , xbi ∈ R are the ground truth and predictions of the i-th future time point.

 

---

C. Processed Data Archive

Going beyond previous work (Ansari et al., 2024; Woo et al., 2024; Liu et al., 2024b), we organized a comprehensive large-scale time series dataset from a vast collection of complex raw data. To ensure data quality, we addressed issues by either imputing missing values or discarding malformed time series. Inspired by data processing techniques from large language models (Penedo et al., 2023; Computer, 2023; Jin et al., 2024), we developed a fine-grained data-cleaning pipeline specifically designed for time series data:

Missing Value Processing.

In time series data, missing values often appear as ‘NaN’ (Not a Number) or ‘Inf’ (Infinity). While previous studies commonly address this by replacing missing values with the mean, this may distort the original time series pattern. Instead, we employ a method that splits the original sequence into multiple sub-sequences at points where missing values occur, effectively removing those segments while preserving the integrity of the original time series pattern.

Invalid Observation Processing.

In some data collection systems, missing values are often filled with 0 or another constant, leading to sequences with constant values that do not represent valid patterns for the model. To address this, we developed a filtering method that uses a fixed-length window to scan the entire sequence. For each window, we calculate the ratio of first-order and second-order differences, discarding the window if this ratio exceeds a pre-specified threshold (set to 0.2 in our case). The remaining valid continuous window sequences are then concatenated into a single sequence. This process transforms the original sequence into multiple sub-sequences, effectively removing segments with invalid patterns.

 

Following the processing steps described above, we compiled a high-quality time series dataset named Time-300B, which spans a range of sampling frequencies from seconds to yearly intervals, encompassing a total of 309.09 billion time points. To optimize memory efficiency and loading speed, each dataset is split into multiple binary files, with a metafile providing details such as the start and end positions of each sequence. This setup allows us to load the data using a fixed amount of memory during training, preventing memory shortages. Datasets like Weatherbench, CMIP6, and ERA5 are particularly large, often leading to data imbalance and homogenization. To mitigate these issues, we apply down-sampling to these datasets. During training, we utilized approximately 117 billion time points in Time-300B, sampling each batch according to fixed proportions of domains and distributions of observation values.

 

Below, we outline the key properties of the datasets after processing, including their domain, sampling frequency, number of time series, total number of observations, and data source. Also, we present the KEY COMPONENT’S SOURCE CODE of the data-cleaning pipeline in Algorithm 2.

 

---

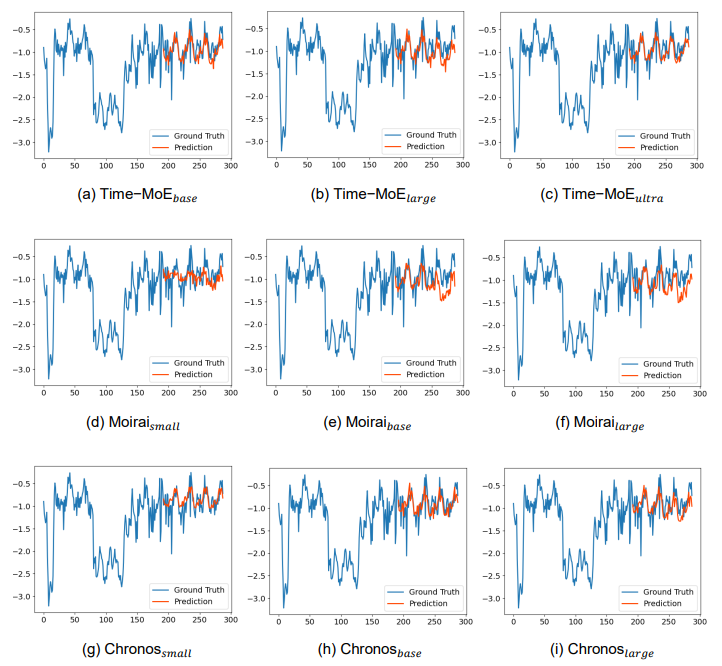
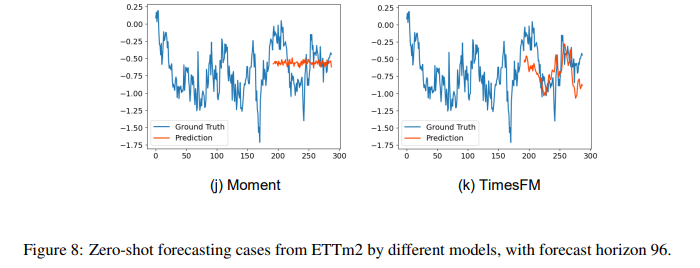
E. Forecast Showcases

To visualize the performance differences among various large-scale time series models, we present the forecasting results of our model, TIME-MOE, in comparison to the ground truth across six realworld benchmarks. These benchmarks include ETTh1, ETTh2, ETTm1, ETTm2, Weather, and Global Temp datasets. Alongside TIME-MOE’s results, we also show the performance of other large-scale baseline models at different scales, providing a comprehensive view of their comparative capabilities (Figures 5 – 10). In all figures, the context length is set to 512, and the forecast horizon is 96. To enhance clarity and aesthetics, we display the full forecast output, complemented by a portion of the preceding historical input data, ensuring a more intuitive comparison.

 

The results clearly demonstrate the superiority of TIME-MOE over the other foundational models. Its ability to consistently produce more accurate forecasts across a range of datasets underscores the effectiveness of its architecture and design. The performance gains are especially noticeable in long-term prediction scenarios, where TIME-MOE’s handling of temporal dependencies proves more robust than its counterparts. These visual comparisons highlight the practical advantages of TIME-MOE in large-scale time series forecasting, reinforcing its status as a state-of-the-art model.

---