-
On Reinforcement Learning and Distribution Matching for Fine-Tuning Language Models with no Catastrophic ForgettingResearch/... 2024. 12. 17. 09:30
https://arxiv.org/pdf/2206.00761
(Nov 2022 NeurIPS 2022)
Abstract
The availability of large pre-trained models is changing the landscape of Machine Learning research and practice, moving from a “training from scratch” to a “finetuning” paradigm. While in some applications the goal is to “nudge” the pre-trained distribution towards preferred outputs, in others it is to steer it towards a different distribution over the sample space. Two main paradigms have emerged to tackle this challenge: Reward Maximization (RM) and, more recently, Distribution Matching (DM). RM applies standard Reinforcement Learning (RL) techniques, such as Policy Gradients, to gradually increase the reward signal. DM prescribes to first make explicit the target distribution that the model is fine-tuned to approximate. Here we explore the theoretical connections between the two paradigms, and show that methods such as KL-control developed for RM can also be construed as belonging to DM. We further observe that while DM differs from RM, it can suffer from similar training difficulties, such as high gradient variance. We leverage connections between the two paradigms to import the concept of baseline into DM methods. We empirically validate the benefits of adding a baseline on an array of controllable language generation tasks such as constraining topic, sentiment, and gender distributions in texts sampled from a language model. We observe superior performance in terms of constraint satisfaction, stability and sample efficiency.

1. Introduction
Pre-trained language models (Devlin et al., 2019; Radford et al., 2019) are changing the landscape of Machine Learning research and practice. Due to their strong generative capabilities many studies have found it sufficient to “nudge” these models to conform to global preferences defined over the generated sequences instead of training from scratch using annotated data. These preferences could include topic and sentiment (Dathathri et al., 2020), valid musical notes and molecular structures (Jaques et al., 2017a), code compilability (Korbak et al., 2021), reducing distributional biases (Khalifa et al., 2021; Weidinger et al., 2021), evaluation metrics for Machine Translation and Summarization (Ranzato et al., 2016; Bahdanau et al., 2016), or direct human feedback (Ziegler et al., 2019; Stiennon et al., 2020). This large body of studies is driven by two different paradigms: Reward Maximization (RM) and Distribution Matching (DM).
Reward Maximization
RM intuitively nudges pre-trained models towards certain preferences by providing global sequence-level rewards when the model generates outputs that satisfy desired features. For instance, if the model is producing toxic content, we can apply Reinforcement Learning (RL) techniques to discourage it from producing similar content. However, naively applying RL yields a model that can undergo catastrophic forgetting of its original distribution. For example, it can degenerate into producing a single nonsensical but at least nontoxic sequence. Although several studies have considered hand-crafting general rewards to ensure desirable features like fluency (Liu et al., 2016a; Tambwekar et al., 2019), coming up with complete or perfect rewards is highly nontrivial (Wu et al., 2016; Vedantam et al., 2015). This has sparked a wide discussion on the overall effectiveness of RM for some tasks such as machine translation (Choshen et al., 2020; Kiegeland & Kreutzer, 2021).
Reward Maximization with KL-Control
To tackle the aforementioned issues of “catastrophic forgetting”, several studies, still under an RM paradigm, have considered incorporating a distributional term inside the reward to be maximized. In particular Jaques et al. (2017b, 2019) and Ziegler et al. (2019) or more recently Stiennon et al. (2020), Ouyang et al. (2022), Bai et al. (2022) and Perez et al. (2022) have applied variations of KL-control (Todorov, 2007; Kappen et al., 2012) which adds a penalty term to the reward term so that the resulting policy does not deviate too much from the original one in terms of KL-divergence. The overall objective with the KL-penalty is maximized using an RL algorithm of choice including: PPO (Schulman et al., 2017a) as in Ziegler et al. (2019) or Bai et al. (2022) or Q-learning (Mnih et al., 2013) as in Jaques et al. (2017b). Adding this distributional KL-penalty to the reward raises some important questions: What effect does it have on the shape of the optimal policy? Does this new objective have any interpretation from a distributional perspective?
Distribution Matching
A different recent paradigm for fine-tuning language models to satisfy downstream preferences formulates the problem as Distribution Matching (DM). This paradigm consists of two steps: first a target distribution incorporating the desired preferences is defined as an Energy-Based Model (LeCun et al., 2006). Then the forward KL divergence is minimized between this target distribution and an auto-regressive policy using a family of algorithms referred to as Distributional Policy Gradients (DPG) (Parshakova et al., 2019b; Khalifa et al., 2021; Korbak et al., 2021, 2022a). This approach capitalizes on the flexibility of EBMs in specifying the target distribution. For example, the EBM can be defined so that it conforms to all downstream preferences while its corresponding normalized distribution has a minimal KL divergence from the original, pre-trained language model, therefore tackling the problem of “catastrophic forgetting” (Khalifa et al., 2021). Interestingly, this DM paradigm can also deal with distributional preferences, for instance, for de-biasing language models by specifying that the generated sequences should be gender-balanced, i.e. that 50% of generations contain female mentions. Such distributional constraints cannot be defined in the RM paradigm where a reward is calculated for a single sequence.
We can notice the promises and limitations of these two paradigms for fine-tuning language models. RM approaches are equipped with an arsenal of RL algorithms and optimization techniques that can be efficient in reward maximization, however they lack the distributional aspect to avoid catastrophic forgetting and impose distributional preferences over LMs. DM approaches are suited to tackle those limitations, however, the family of DPG algorithms currently used is not as rich as its RL counterpart.
While the connections between these two seemingly distinct paradigms have been noted (Parshakova et al., 2019b; Korbak et al., 2022b), they have not been explored in detail. Clarifying such connections might help import ideas from one approach to the other. This is our goal in this paper, detailing the nuanced connections and applying them to a case-study in variance reduction. Overall, our contributions are the following:
• We clarify relations between the RM and DM paradigms through a detailed comparison between the family of DPG algorithms and Policy Gradients (Table 1), stressing the differences between parametric and non-parametric rewards that are important in this regard.
• We introduce an interpretation of KL-control techniques from a distribution matching perspective, placing such techniques at an intermediate place between RM and DM (Theorem 1).
• We show how these connections can enable cross-pollination between the two perspectives by applying baselines — a variance reduction technique from RL — to DPG and derive a particular choice of a baseline (Facts 1 and 2). On an array of controllable language generation experiments, we show that adding baselines leads to superior performance on constraint satisfaction (Figure 3), stability on small batch sizes, and sample efficiency (Figure 4).
2. Background
Standard Policy Gradients
One popular method for adapting the behaviour of language models to certain preferences has been that of assigning a “reward” score R(x) for sequences x sampled from an autoregressive language model (policy) πθ. Then, the simplest policy gradient algorithm in reinforcement learning, namely, REINFORCE (Williams, 1992a), aims to find the policy πθ(x) that maximizes the average reward Ex∼πθR(x), and this leads, via the so-called “log derivative trick”, to a gradient ascent algorithm that iteratively samples x from πθ and update parameters by increments proportional to R(x)∇θ log πθ(x) via the following identity:

KL-control
(Todorov, 2007; Kappen et al., 2012), was leveraged by Jaques et al. (2017b, 2019) and Ziegler et al. (2019) to include a KL penalty term in the reward function to penalize large deviations from the original pretrained model a(x), weighted by a free hyperparameter β to control the trade-off between the two goals. That is, they maximize the expectation E x∼πθ R^z_θ (x), where:

Distributional Policy Gradients (DPG)
(Parshakova et al., 2019b) is a recent approach used to fit an autoregressive policy πθ to the distribution p(x) = P(x)/Z induced by the EBM P(x), where Z = summation_x P(x) is the normalization constant (partition function). Given an arbitrary EBM P(x), DPG optimizes the loss function DKL(p, πθ) with respect to the parameters θ of an autoregressive model πθ, a loss which is minimized for πθ = p. The KL-divergence minimization objective leads to a gradient estimate of the form:

3. Reward Maximization vs Distribution Matching
In the previous section, we have summarized three approaches that have been suggested for fine-tuning language models. Two of them can be characterized as “Reward Maximization” (RM): Standard Policy Gradients (PG) and KL-control. On the other hand, DPG clearly belongs to the realm of “Distribution Matching” (DM) as it first defines the target distribution and then optimizes a policy to match it. In the rest of this section, we will explore connections between these two seemingly distinct concepts and, in the following section, we will exploit them to improve DM-based methods.
3.1. Standard vs. Parametric Rewards
Let us start with distinguishing between a “parametric reward” Rθ which depends on θ and a standard reward R, which does not. If we wished to maximize the expected parametric reward, E πθ Rθ(x), we would follow its gradient, leading to the identities:

Equation (8) is the sum of two terms: the first one, the “RG-term" (Reward Gradient term), involves the gradient of the reward. The second one, the “PG-term” (Policy Gradient term), was obtained using the “log derivative trick” and involves the gradient of the policy stricto sensu. In standard RL, where the reward does not depend on θ, the RG-term disappears and the gradient of expected reward consists solely of the PG-term. However, when Rθ depends on θ, the gradients are distinct (apart from specific cases where the RG-term evaluates to 0, as we will see below).
3.2. KL-control as Distribution Matching
Adding a KL-penalty term to the reward (as in the case of KL-control) leads to a parametric reward. However, due to the particular form of its objective, the RG-term actually vanishes, 3 leaving only the PG-term

and simplifying the tuning procedure to a standard Policy Gradient. While this algorithm falls under the RM paradigm, here we argue that is its nature is multifaceted, and explore deeper connections with the DM paradigm. More precisely, the maximization of reward with the KL penalty term is equivalent to a distributional matching with an underlying emergent sequential EBM, a remark that already reveals some similarities with DPG.4
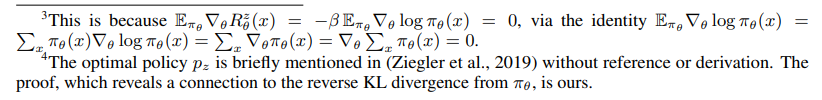


Overall, we can conclude that the addition of the distributional term (KL-penalty) to the reward does indeed provide a DM interpretation, namely in terms of minimizing the reverse KL divergence with an emergent underlying distribution p_z(x). We note that p_z(x) does not correspond to a free and explicit choice of EBM (e.g. one that balances the gender and topic distributions of a language model). Instead equation (9) appears in a restrictive format, which is implicitly defined by the reward R^z_θ, along with a β hyperparameter without a clear meaning. By contrast, the DPG algorithms are designed to perform DM on any EBM specification, corresponding to an explicit distributional objective.

3.3. Similarities and Differences between DPG and Policy Gradients

4. A Case Study on Variance Reduction
Baselines are a standard variance reduction technique in the context of Policy Gradients (Sutton & Barto, 2018). The idea is to subtract from the reward R(x) a value B that does not introduce bias to the gradients but may change variance. After the introduction of baseline, equation (1) then takes the following form:



4.1. Generation with Distributional Control
We investigate the benefits of adding a baseline to the DPG algorithm, on the Generation with Distributional Control (GDC) (Khalifa et al., 2021) framework. GDC makes use of DPG to control the properties of pre-trained language models to satisfy certain constraints. In our experiments, follow target distribution form of Parshakova et al. (2019a), Khalifa et al. (2021) and Korbak et al. (2022a), in which the EBM P(x) is defined so that its normalized variant p(x) matches a set of desired moments constraints on given features φi(x), while having a minimal KL divergence DKL(p, a) from an original pretrained language model a, to avoid catastrophic forgetting.
These constraints are expressed as conditions µ¯i = Ex∼pφi(x), for i ∈ {1, . . . , n}, by which the moments (expectations) under the distribution p of each feature φi(x) are required to take certain desired values µ¯i . For instance, let φ1(x) = 1 iff the topic of x is science and φ2(x) = 1 iff x mentions a female person, then imposing moments µ¯1 = 1 and µ¯2 = 0.5 constrains the language model p to only generate sequences about science, half of which mention females. P(x) is uniquely determined by the following form:7

where λi terms control the moments µi of the associated features, which can be estimated through self-normalized importance sampling (Owen, 2013); and then, to make the moments match the desired values, the λi terms can be optimized through SGD (Parshakova et al., 2019a).
4.2. Experimental setup
We evaluate our method on an array of 10 controlled text generation tasks. For each, given a pretrained language model a(x), and a set of constraints, the objective of each fine-tuning method is to obtain a fine-tuned language model πθ that satisfies the imposed constraints while deviating as minimally as possible from the original language model a(x).
Constraints are defined as a set of binary features {φi} and their corresponding desired percentages (moments) {µ¯i} within the generations of the target language model. Based on the value of the moment constraints these 10 tasks are divided into 6 tasks of pointwise constraints (for which µ¯i = 1), 2 tasks of distributional constraints (0 < µ¯i < 1) and 2 tasks of mixed type constraints (hybrid):
(a) Single-word constraints, where φ(x) = 1 iff the a given word appears in the sequence x. We experiment with frequent words (task 1: “amazing”, original frequency: 10^−4 ) and (task 2: “WikiLeaks”, original frequency: 10^−5 ) rare words,
(b) Wordlist constraints, where φ(x) = 1 iff x contains at least one word from a given list. We consider lists of word associated with politics (task 3) and science (task 4) published by Dathathri et al. (2020),
(c) Sentiment classifier constraints, where φ(x) = 1 if x is classified as positive (task 5), or negative (task 6) by a pre-trained classifier published by Dathathri et al. (2020).
(d) A single distributional constraint where φ(x) = 1 iff x contains a female figure mention, and µ¯ = 0.5 (task 8),
(e) A set of four distributional constraints: φi(x) = 1 iff x contains at least one of the words in the “science", “art", “sports" and “business" wordlists (compiled by Dathathri et al. (2020)), respectively. For each i, µ¯i = 0.25 (task 8),
(f) Hybrid constraints where φ1(x) = 1 iff x contains more female than male pronouns, µ¯1 = 0.5 and φ2(x) = 1 iff x contains at least one of the words from the “sports" wordlist (task 9) or “politics” wordlist, µ¯2(x) = 1 (task 10).
Methods
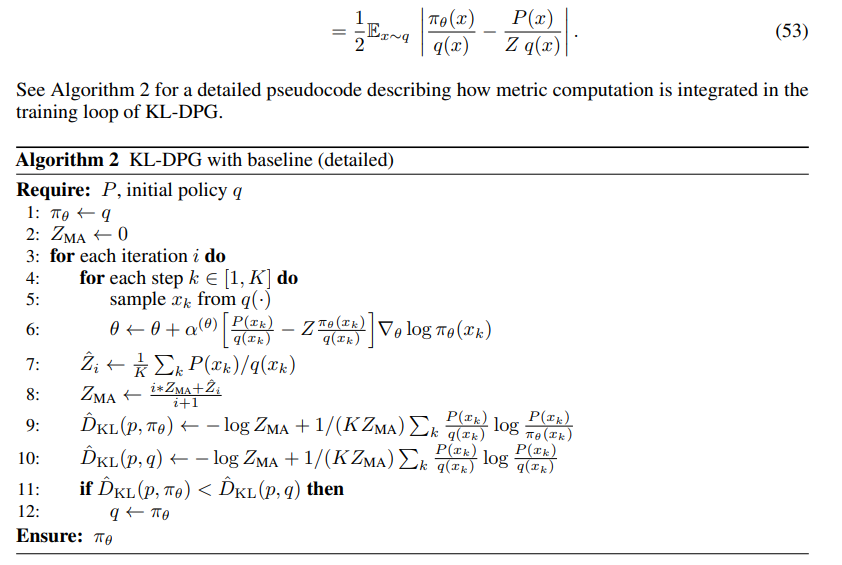
We modify the GDC framework Khalifa et al. (2021), namely its KL-DPG algorithm, to include a baseline as shown in Algorithm 1. We refer to this method as GDC++. In addition to comparing GDC++ with GDC we compare with two reward maximization baselines: Reinforce (Williams, 1992b) and Ziegler (Ziegler et al., 2019). Reinforce tries to maximize the expected reward Ex∼πθR(x), where R(x) = 1 if and only if the pointwise constraints are met. Ziegler instantiates the KL-control approach: its objective includes a KL penalty term for departures from a. Following (Khalifa et al., 2021), for hybrid and distributional constraints (tasks 8-10) we compare only GDC and GDC++ because the RM objective of Ziegler and Reinforce is not equipped to handle them.
Metrics
We report the following metrics at each validation step over batches of samples from πθ:
1. Ex∼πθ φi(x), measuring the ability to reach the target moment of the i-th feature.
2. DKL(p, πθ), the forward KL divergence from the optimal target distribution p, 8
3. DKL(πθ, a), the reverse KL divergence from the original pretrained language model a.
4. Distinct-n score, a measure of text diversity in terms of the frequency of repetitions within a single sample x, proposed by (Li et al., 2016a).
5. Self-BLEU-n, a measure of text diversity on a distributional level across samples proposed by (Zhu et al., 2018), ensuring that policies don’t converge into limited number of sequences that satisfy the imposed constraints Caccia et al. (2020).
Training details
For tasks 1-6, we use a pre-trained GPT-2 small with 117M parameters (Radford et al., 2019) as the original language model a. For tasks 7-10, a is the same pre-trained model additionally fine-tuned on the WikiBio (Lebret et al., 2016) dataset. See Appendix E for more details. The code for all the experiments presented in the paper will be available at github.com/naver/gdc.
4.3. Results
We present the evolution of our metrics through training epochs in Figure 3 (aggregated over tasks 1-6) and Figure 6 in the Appendix (aggregated over tasks 7-10). Results for each task are presented separately on Figures 7-10 in the Appendix.

Consistent with prior work (Khalifa et al., 2021; Korbak et al., 2022a), we observe that Reinforce is able to quickly achieve high levels of constraint satisfaction, but at the cost of large deviations from a, which translates into significantly decreased diversity of generated samples (in terms of Self-BLEU-5 and Distinct-1). The KL penalty term in Ziegler imposes an upper bound on deviation from a but the deviation is still significant enough to result in a drop in diversity. Moreover, we have observed Ziegler’s objective to result in very unstable training.
GDC and GDC++ are the only fine-tuning methods that address constraint satisfaction based on a clear formal objective, i.e. reducing the divergence from p. The approach translates into significantly smaller deviations from a and maintaining diversity within and across samples. The addition of a baseline indeed reduces the variance. We analyze that extensively in Appendix 4.5 while here focusing on the downstream effects of variance reduction. One is that πθ is now able to compound staying closer to p and a at the same time, while achieving slightly better constraint satisfaction. We have also observed that baseline stabilizes training, leading to smoother curves.9
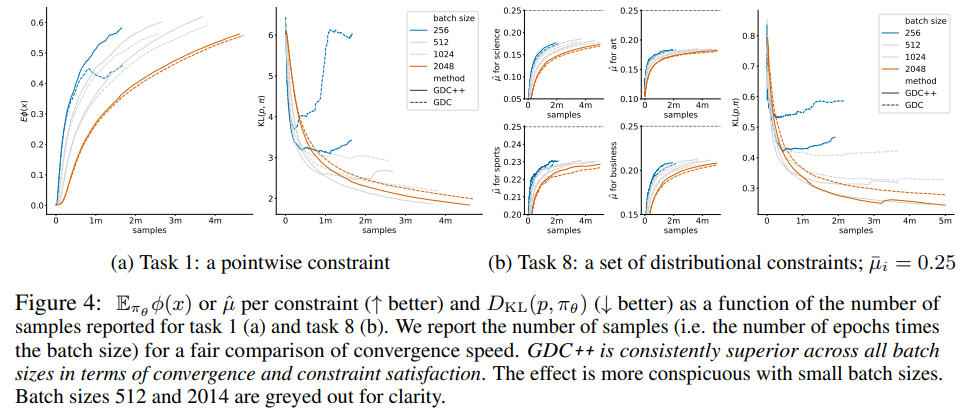
4.4. The effect of baseline across batch sizes
We expect that reducing gradient estimates variance can allow to train with lower batch sizes, performing gradient updates on estimates based on smaller batch sizes can increase the sample efficiency. To test this, we rerun tasks 1 (a pointwise constraint on the word “amazing") and 8 (distributional constraints on topics) with four batch sizes (256, 512, 1024, 2048). Figures 4a and 4b show the benefits of adding a baseline — higher constraint satisfaction, lower divergence from p, more stable training — and is especially evident with lower batch sizes. For instance, with batch size 256, GDC++ obtains a significantly higher constraint satisfaction rate and lower divergence from p.
Furthermore, stable training with smaller batch sizes translates into better sample efficiency. For instance, in task 1 (Figure 4a), GDC++ with batch size 256 needs 1M samples to achieve Ex∼πθ φ(x) = 0.5 while GDC++ with batch size 2048 needs 4M. In contrast, GDC with batch size 256 does not achieve Ex∼πθ φ(x) = 0.5 at all, confirming the importance of adding the baseline.
4.5. Empirical Evaluation of Variance Reduction

It directly provides a standard measure of distributional discrepancy between p and πθ, in terms of TVD (Total Variation Distance). We have:
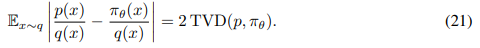
Results Figure 5 shows that GDC++ obtains lower variance in the gradient estimates Var(Gθ) and the variance of the advantage Var (A) in both pointwise and distributional experiments compared to its non-baseline counterpart GDC. We further observe a decreasing trend in the mean absolute value of the advantage µ^|A| which is correlated with a decreasing trend in the TVD distance between the trained policy πθ and the optimal distribution p. Overall, these results shows that adding a baseline to DPG reduces the variance during training and yields better convergence towards the optimal distribution p.
5. Related work
The idea of posing control problems as distribution matching has resurfaced numerous times in the RL literature (Kappen et al., 2012; Friston et al., 2010; Levine, 2018; Hafner et al., 2020; Buckley et al., 2017). KL-control can be seen as a generalisation of maximum entropy RL (MaxEnt RL) (Haarnoja et al., 2017, 2018) to informed priors. If in (2) we chose a(x) to be a uniform distribution (assuming right now finiteness of X) instead of a pretrained LM distribution, then the KL penalty DKL(πθ, a) would reduce to an entropy bonus. Both KL-control and MaxEnt RL can be derived from a general framework of control-as-inference (Levine, 2018) which poses control as minimising KL from a certain target distribution. However, most practical algorithms in the MaxEnt RL family minimise KL from a target policy which changes throughout training; in contrast, DPG’s target distribution p and KL-control implicit target distribution pz are defined at trajectory level and fixed throughout training.
Perhaps the closest method to KL-control and DPG in the larger family of inference-based RL (Furuta et al., 2021) is AWR (Peng et al., 2019) which minimises the forward KL from an off-policy target distribution. Yet another approach with apparent similarity to KL-control and DPG is state marginal matching (SMM) (Hazan et al., 2018; Lee et al., 2019). SMM poses exploration as learning a policy that induces a state marginal distribution that matches a target state distribution. While SMM’s target distribution is fixed, it is defined for individual states, while in the controllable language generation tasks we consider, the target distribution is defined over a complete trajectory considered as a unit. See Appendix B for an extended discussion of related work.
6. Conclusion
Fine-tuning large language models has become an active area of research, due to its importance in adapting large language models to satisfy task-level preferences, or in combating their social risks such as “distributional” stereotyping (Weidinger et al., 2021; Welbl et al., 2021). 10 In this paper, we analyzed in depth the nuanced relation between two popular fine-tuning paradigms: RM and DM. We demonstrated that KL-control can be seen as a form of DM and showed that while DPG and PG have different goals, some similarities (similar forms of gradient estimates despite different objectives) can be exploited. We used these insights to inform an extension of DPG, consisting in adding a baseline to reduce the variance of gradient estimates.
The connections we established suggest that despite fundamental differences between DPG and RL, some of the theoretical results and algorithmic techniques from RL can be adapted to a DM framework without losing their formal guarantees. In this paper, we focus on variance reduction using baselines, but the space of possible enhancements is vast. Promising candidates include further reducing the variance using a learned value function (Konda & Tsitsiklis, 2000) and preventing detrimentally large policy updates by maintaining a trust region in the policy space – akin to techniques such as TRPO (Schulman et al., 2015) and PPO (Schulman et al., 2017b). Another future direction could consist in analyzing the relation between explicit EBMs in DPG and implicit EBMs arising in KL-control and characterizing the space of EBMs that could be reached through KL-control.
A. Broader impacts
The focus area of this paper — fine-tuning large language models — is aligned with an important line of work on addressing the problem of social bias in large language models (Sheng et al., 2019; Liang et al., 2021). As the training data for large language models consists mainly of crawled user-generated content, a number of factors (from crawling methodology to Internet participation inequalities and moderation practices) leads to an over-representation of certain viewpoints and voices exceeding their prevalence in the general population. This poses a risk of amplifying biases and harms through a language model perpetuating these voices (Bender et al., 2021; Blodgett et al., 2020; Sheng et al., 2019; Weidinger et al., 2021; Welbl et al., 2021). Numerous problems related to addressing data bias in language generation (e.g. controlling for gender distribution in generated texts) can be naturally posed as generative distributional control (GDC), the framework we focus our experiments on. The distributional character of these data bias problems lies in the fact that desirable properties of generated texts are defined for a collection of samples, not only for individual samples. Our theoretical analyses of reward maximization and distribution matching approaches as well as our algorithmic improvements to the GDC framework — termed GDC++ — are therefore also a contribution to the problem of bias in language models. However, we need to be aware that GDC++ , KL-control as well as controllable language generation techniques in general, can also be diverted to malicious uses such as spreading misinformation or generating harmful content.
B. Extended Related Work
Reinforcement learning for language generation
Most previous attempts at steering language models to conform to global constraints defined over entire sequences have employed reinforcement learning. This includes using Reinforce (Williams, 1992a) for machine translation Ranzato et al. (2016), actor critic (Konda & Tsitsiklis, 2000) for abstractive summarization (Paulus et al., 2018), caption generation (Liu et al., 2016b), dialogue (Li et al., 2016b), and video captioning (Pasunuru & Bansal, 2017). Some approaches (for instance, in machine translation and summarization (Ranzato et al., 2016; Bahdanau et al., 2017)) directly optimize performance metrics such as BLEU and ROUGE at training time. Others use heuristic rewards (for instance Li et al. (2016b) for dialogue generation and Tambwekar et al. (2019) for story generation) in order to obtain certain a priori desirable features of generated sequences that then incentivize good performance on target metrics. Catastrophic forgetting is a frequent problem of these fine-tuning approaches: reward maximization happens at the expense of large deviations from the original model. This problem is sometimes addressed by imposing a penalty term to the rewards, such as the KL divergence between the trained policy and the auto-regressive model. This approach, termed “conservative fine-tuning", was applied to generating melodies with music theory rewards and organic molecules with synthesizability rewards by Jaques et al. (2017a) as well fine-tuning language models for controllable language generation by Ziegler et al. (2019). This solution often has hard time balancing between the reward term and the KL penalty term, leading to instability in training (Khalifa et al., 2021; Korbak et al., 2022a). Unlike this approach, KL-DPG determines an optimal distribution that satisfies both requirements.
RM and DM objectives in control problems
While RM is the dominant approach to tackling control problems (Sutton & Barto, 2018) and is sometimes argued to be sufficient for any intelligent behavior (Silver et al., 2021), prior work explored the benefits of alternative objectives formulated as DM: minimizing divergence from some target distribution p. Prominent examples of (families of) DM objectives include control state marginal matching (Lee et al., 2019) active inference (Friston et al., 2010; Buckley et al., 2017) and control-as-inference (Kappen et al., 2012; Todorov, 2007; Levine, 2018). Hafner et al. (2020) propose a reverse KL from a joint distribution over observations and latent variables as a universal objective for action and perception that — depending on a choice of the target p — gives rise to many familiar objectives, including empowerment (Klyubin et al., 2005), maximum entropy RL (Haarnoja et al., 2017) or KL-control (Todorov, 2007). In a similar vein, Millidge et al. (2021) compare RM and DM objectives (or, evidence and divergence objectives, according to their terminology) in the context of exploration. They conclude that information-seeking exploration arises naturally in DM but not in RM. This is because, when the target distribution p involves latent variables, a DM objective decomposes into an information gain term that pushes the agent to seek observations that are most informative of latent variables. In contrast, RM objectives entail minimizing information gain between latent variables and observations. Finally, (Korbak et al., 2022b) defend an interpretation of KL-control for controlling language models as Bayesian inference: updating a prior a to conform to evidence provided by a reward function R.
Baselines in Reinforcement Learning
In the context of reinforcement learning, baselines were introduced by Sutton (1984). Williams (1987, 1992a) has shown them to reduce variance in a number of use cases and also proved that they do not introduce bias. Dayan (1990) was the first to observe and confirm experimentally that the optimal constant baseline is not equal to expected reward in a simple two-arm bandit setting. This result was generalized to POMDPs (Partially Observable Markov Decision Processes) by Weaver & Tao (2001, section 3.1.3, p. 540) and variable baselines by Greensmith et al. (2004, theorem 13, p. 1489) who also proved bounds on the variance of gradient estimates. The optimal baseline, however, is rarely used in practice (Sutton & Barto (2018); for an exception, see (Peters & Schaal, 2008)). Outside RL, baselines were also used in the context of learning inference networks for amortized variational inference by Mnih & Gregor (2014) and found to yield similar variance reduction.
Energy-based models for language
Energy-based models (EBMs) (Hinton, 2002; LeCun et al., 2006; Ranzato et al., 2007) are a family of models in which learning and inference are done by associating an unnormalized probability with each configuration of observed and latent variables. Early examples of EBMs applied to natural language processing include sequence labeling problems (e.g. tagging) exploiting global properties of a sequence (Andor et al., 2016; Belanger & McCallum, 2016). The recent surge of interest in EBMs has not left natural language processing unaffected (see Bakhtin et al. (2020) for a survey). Tu et al. (2020) proposed an energy-based inference networks for non-autoregressive machine translation while Naskar et al. (2020) use an EBM for reranking candidate translations according to their predicted BLEU scores. Parshakova et al. (2019a) and Deng et al. (2020) augment an autoregressive language models with an additional global factor to obtain a lower perplexity on the training data. Clark et al. (2020) poses non-autoregressive language modeling as training an energy-based cloze task scorer using noise-contrastive estimation (Gutmann & Hyvärinen, 2010). He et al. (2021) obtain better calibration on natural language inference tasks by augmenting and training the classifier jointly with an energy-based model modeling the marginal distribution over samples, again using noise-contrastive estimation. In consequence, the classifier tends to assign more conservative (high-entropy) predictions to high-energy (less likely, possibly out of distribution) samples.
C. Additional proofs
C.2. unbiasedness of PG baseline
Baselines are a standard variance reduction technique in the context of Policy Gradients (Sutton & Barto, 2018). The idea is to subtract from the reward R(x) a value B that does not introduce bias to the gradients but may change variance. Equation (1) then takes the following form:

To see that B does not introduce bias, we can rewrite (11) as:
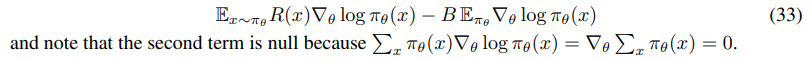
C.3. Unbiasedness of DPG Baseline
Recall that the gradient estimate for DPG (Parshakova et al., 2019a) has the following form:

After subtracting a baseline B = Z, it becomes

C.4. Unbiasedness of DPG^off baseline
Offline DPG, the off policy variant of DPG proposed in Parshakova et al. (2019b); Khalifa et al. (2021) has the following gradient estimate:

Where q is a proposal distribution (another auto-regressive model) used to detach the training of πθ from the sampling process and allow more stable training.
Recall that the Baseline of DPG^off is of the form:


To visualize things better, we elaborate the difference in forms of rewards, baseline and gradients before and after addition of the baseline between DPG (on policy) and DPGoff (off policy) in Table 2.

D. Additional details on metrics and Algorithms

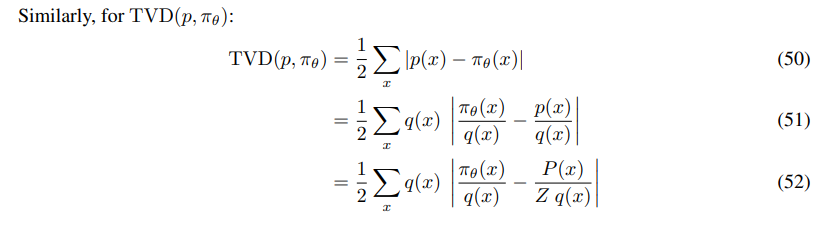
'Research > ...' 카테고리의 다른 글
(2/3) GAN, F-Divergence, IPM (0) 2024.12.21 (1/3) GAN, F-Divergence, IPM (0) 2024.12.20 DPG (0) 2024.12.17 [DPG] Distributional Reinforcement Learning for Energy-Based Sequential Models (0) 2024.12.12 A Distributional Approach to Controlled Text Generation (0) 2024.12.09