[VDMs] 계속 등장하는 수식들

https://arxiv.org/pdf/2401.06281

나중에 참고하려고 정리

 

여러 번 line by line으로 도출해봄..

---

2.1. Forward Process: Gaussian Diffusion

2.1.1. Linear Gaussian Transitions: q(zt | zs)

 

---

2.1.2. Top-down Posterior: q(zs | zt, x)

---

---

2.1.3. Learning the Noise Schedule

---

2.2. Reverse Process: Discrete-Time Generative Model

2.2.1. Generative Transitions: p(zs | zt)

 

Two other notable parameterizations not elaborated upon in this article but certainly worth learning about include v-prediction (Salimans and Ho, 2022), and F-prediction (Karras et al., 2022). There are also interesting links to Flow Matching (Lipman et al., 2023), specifically with the Optimal Transport (OT) flow path, which can be interpreted as a type of Gaussian diffusion. Kingma and Gao (2023) formalize this relation under what they call the o-prediction parameterization – for further details on this and more the reader may refer to appendix D.3 in Kingma and Gao (2023).

---

---

---

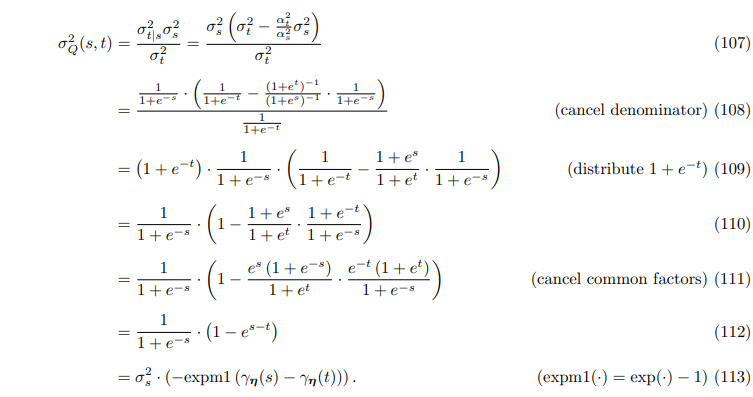
2.2.2. Variational Lower Bound

---

2.2.3. Deriving D_kl( q(zs | zt, x) || p(zs | zt) )

---

---

2.2.4. Monte Carlo Estimator of L_T(x)

---

2.3. Reverse Process: Continuous-Time Generative Model

2.3.1. On Infinite Depth

Kingma et al. (2021) showed that doubling the number of timesteps T always improves the diffusion loss, which suggests we should optimize a continuous-time VLB, with T → ∞.

---

2.3.2. Monte Carlo Estimator of L_∞(x)

---

2.3.3. Invariance to the Noise Schedule

---

2.4. Understanding Diffusion Objectives

In Sections 2.2 and 2.3 we established that when the weighting function is uniform, diffusion-based objectives correspond directly to the ELBO.

 

Although weighted diffusion model objectives appear markedly different from the ELBO, it turns out that all commonly used diffusion objectives optimize a weighted integral of ELBOs over different noise levels. Furthermore, if the weighting function is monotonic, then the diffusion objective equates to the ELBO under simple Gaussian noise-based data augmentation (Kingma and Gao, 2023). Different diffusion objectives imply specific weighting functions w(·) of the noise schedule.

---

2.4.1. Weighted Diffusion Loss

 

---

2.4.2. Noise Schedule Density

---

2.4.3. Importance Sampling Distribution

---

2.4.4. ELBO with Data Augmentation

---