Metropolis-Hastings algorithm

---

※ Taboga, Marco (2021). "Metropolis-Hastings algorithm", Lectures on probability theory and mathematical statistics. Kindle Direct Publishing. Online appendix.

https://www.statlect.com/fundamentals-of-statistics/Metropolis-Hastings-algorithm

---

The Metropolis-Hastings algorithm is one of the most popular Markov Chain Monte Carlo (MCMC) algorithms.

 

Like other MCMC methods, the Metropolis-Hastings algorithm is used to generate serially correlated draws from a sequence of probability distributions. The sequence converges to a given target distribution.

---

Preliminaries

Before reading this lecture, you should review the basics of Markov chains and MCMC.

 

In particular, you should keep in mind that an MCMC algorithm generates a random sequence {X_t} having the following properties:

• it is a Markov chain (given X_t, the subsequent observations X_t+n are conditionally independent of the previous observations X_t-k, for any positive integers k and n).
• two observations X_t and X_t+n are in general not independent, but they become closer and closer to being independent as n increases;
• the sequence converges to the target distribution (the larger t is, the more the distribution of X_t is similar to the target distribution).

When we run an MCMC algorithm for T periods, we obtain an MCMC sample made up of the reailizations of the first T terms of the chain:

x1, ..., xT

 

Then we use the empirical distribution of the sample to approximate the target distribution.

---

The algorithm

Let f(x) be the probability density (or probability mass) function of the distribution from which we wish to extract a sample of draws. We call f(x) the target distribution.

 

Denote by q(x|x') a family of conditional distributions of our choice, from which it is easy to generate draws.

 

The vectors x, x' and the argument of f(x) all have the same dimension.

 

The Metropolis-Hastings algorithm starts from any value x1 belonging to the support of the target distribution. The value x1 can be user-defined or extracted from a given distribution.

 

The, the subsequent values x2, ...xT are generated recursively.

---

Terminology

The following terminology is used:

---

Metropolis algorithm

---

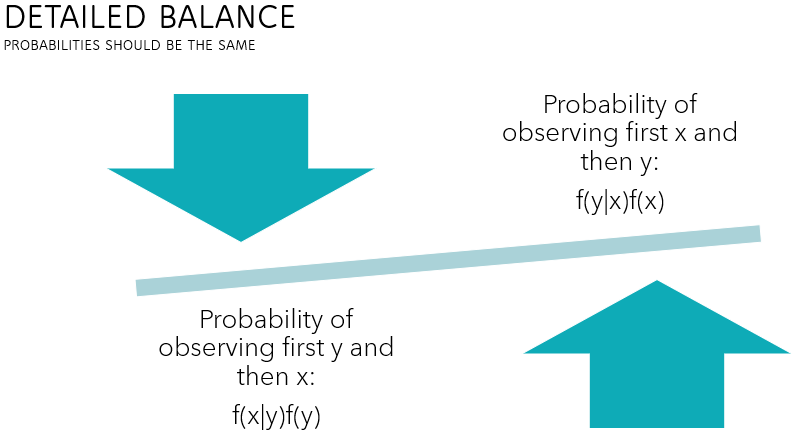
Detailed balance

The crucial step is to prove that the so-called detailed balance condition holds, which implies that the target distribution is the stationary distribution of the Markov chain generated by the Metropolis-Hastings algorithm.

 

---

Technical conditions

When we proved the detailed balance condition, we omitted an important detail: the proposal distribution must be able to generate all the values belonging to the support of the target distribution.

 

This is intuitive: if the proposal distribution never generates a value x_t to which the target distribution assigns a positive probability, then certainly the stationary distribution of the chain cannot be equal to the target distribution.

---

Multiplicative constants

As already shown in the introductory lecture on MCMC methods, one of the main advantages of the Metropolis-Hastings algorithm is that we need to know the target distribution f only up to a multiplicative constant.

 

This is very important in Bayesian inference, where the posterior distribution is often known up to a multiplicative constant (because the likelihood and the prior are known but the marginal distribution is not).

 

So, we do not need to know the constant c to compute the acceptance probability, and the latter is the only quantity in the algorithm that depends on the target distribution f.

 

Therefore, we can use the Metropolis-Hastings algorithm to generate draws from a distribution even if we do not fully know the probability density (or mass) of that distribution!