Metropolis and Gibbs Sampling

※ https://people.duke.edu/~ccc14/sta-663-2018/notebooks/S10D_MCMC.html

---

Introduction to MCMC

In regular Markov chain models, we are usually interested in finding the equilibrium distribution Tπ at which

for a given transition kernel T.

 

MCMC inverts this thinking - we fix the equilibrium distribution to be the posterior distribution

 

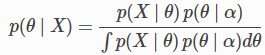
and look for a transition kernel that will converge to this equilibrium distribution.

---

Island hopping

We first provide an example to show the mechanics of the Metropolis algorithm concretely, then explore why it works.

 

Kruschke's book begins with a fun example of a politician visiting a chain of islands to canvas support - being callow, the politician uses a simple rule to determine which island to visit next. Each day, the politician chooses a neighboring island and compares the populations there with the population of the current island. If the neighboring island has a larger population, the politician goes over. If the neighboring island has a smaller population, then the politician visits with probability p=p_neighbor / p_current; otherwise the politician stays on the same island. After doing this for many days, the politician will end up spending time on each island proportional to the population of each island - in other words, estimating the distribution of island populations correctly. How a simple comparison of only two states at a time can lead to accurate estimation of a probability density is the topic of the next few lectures.

---

%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
from functools import partial

sns.set_context('notebook', font_scale=1.5)

def make_islands(n, low=10, high=101):
    islands = np.random.randint(low, high, n+2)
    islands[0] = 0
    islands[-1] = 0
    return islands

def hop(islands, start=1, niter=1000):
    pos = start
    pop = islands[pos]
    thetas = np.zeros(niter+1, dtype='int')
    thetas[0] = pos
    for i in range(niter):
        # generate sample from proposal distribution
        k = np.random.choice([-1, 1], 1)
        next_pos = pos + k
        # evaluate unnormalized target distribution at proposed position
        next_pop = islands[next_pos]
        # calculate acceptance probability
        p = min(1, next_pop/pop)
        # use uniform random to decide accept/reject proposal
        if np.random.random() < p:
            pos = next_pos
            pop = next_pop
        thetas[i+1] = pos
    return thetas

islands = make_islands(10)
thetas = hop(islands, start=1, niter=10000)

True population proportions

data = islands[1:-1]
data = data/data.sum()
sns.barplot(x=np.arange(len(data)), y=data)
pass

Estimated population proportions

data = np.bincount(thetas)[1:]
data = data/data.sum()
sns.barplot(x=np.arange(len(data)), y=data)
pass

Generic Metropolis scheme

def metroplis(start, target, proposal, niter, nburn=0):
    current = start
    post = [current]
    for i in range(niter):
        proposed = proposal(current)
        p = min(target(proposed)/target(current), 1)
        if np.random.random() < p:
            current = proposed
        post.append(current)
    return post[nburn:]

Apply to island hooper

target = lambda x: islands[x]
proposal = lambda x: x + np.random.choice([-1, 1])
post = metroplis(1, target, proposal, 2000)
data = np.bincount(post)[1:]
data = data/data.sum()
sns.barplot(x=np.arange(len(data)), y=data)
pass

---

Bayesian Data Analysis

---

Motivating example

We will use the toy example of estimating the bias of a coin given a sample consisting of n tosses to illustrate a few of the approaches.

Analytical solution

If we use a beta distribution as the prior, then the posterior distribution has a closed form solution. This is shown in the example below. Some general points:

• We need to choose a prior distribution family (i.e. the beta here) as well as its parameters (here a=10, b=10)
• The prior distribution may be relatively uninformative (i.e. more flat) or informative (i.e. more peaked)
• The posterior depends on both the prior and the data
• As the amount of data becomes large, the posterior approximates the MLE
• As informative prior takes more data to shift than an uninformative on
• Of course, it is also important the model used (i.e. the likelihood) is appropriate for the fitting the data
• The mode of the posterior distribution is known as the maximum a posteriori (MAP) estimate (cf MLE which is the mode of the likelihood)

import scipy.stats as stats

n = 100
h = 61
p = h/n
rv = stats.binom(n, p)
mu = rv.mean()

a, b = 10, 10
prior = stats.beta(a, b)
post = stats.beta(h+a, n-h+b)
ci = post.interval(0.95)

thetas = np.linspace(0, 1, 200)
plt.plot(thetas, prior.pdf(thetas), label='Prior', c='blue')
plt.plot(thetas, post.pdf(thetas), label='Posterior', c='red')
plt.plot(thetas, n*stats.binom(n, thetas).pmf(h), label='Likelihood', c='green')
plt.axvline((h+a-1)/(n+a+b-2), c='red', linestyle='dashed', alpha=0.4, label='MAP')
plt.axvline(mu/n, c='green', linestyle='dashed', alpha=0.4, label='MLE')
plt.xlim([0, 1])
plt.axhline(0.3, ci[0], ci[1], c='black', linewidth=2, label='95% CI');
plt.xlabel(r'$\theta$', fontsize=14)
plt.ylabel('Density', fontsize=16)
plt.legend(loc='upper left')
pass

Numerical integration

One simple way of numerical integration is to estimate the values on a grid of values for θ. To calculate the posterior, we find the prior and the likelihood for each value of θ, and for the marginal likelihood, we replace the integral with the equivalent sum

 

One advantage of this is that the prior does not have to be conjugate (although the example below uses the same beta prior for ease of comparison), and so we are not restricted in our choice of an appropriate prior distribution. For example, the prior can be a mixture distribution or estimated empirically from data. The disadvantage, of course, is that this is computationally very expensive when we need to estimate multiple parameters, since the number of grid points grows as O(n^d), where n defines the grid resolution and d is the size of θ.

thetas = np.linspace(0, 1, 200)
prior = stats.beta(a, b)

post = prior.pdf(thetas) * stats.binom(n, thetas).pmf(h)
# Normalzie so volume is 1
post /= (post.sum() / len(thetas))

plt.plot(thetas, prior.pdf(thetas), label='Prior', c='blue')
plt.plot(thetas, n*stats.binom(n, thetas).pmf(h), label='Likelihood', c='green')
plt.plot(thetas, post, label='Posterior', c='red')
plt.xlim([0, 1])
plt.xlabel(r'$\theta$', fontsize=14)
plt.ylabel('Density', fontsize=16)
plt.legend()
pass

---

Markov Chain Monte Carlo (MCMC)

This lecture will only cover the basic ideas of MCMC and the 3 common variants - Metroplis, Metropolis-Hastings and Gibbs sampling. All code will be built from the ground up to illustrate what is involved in fitting an MCMC model, but only toy examples will be shown since the goal is conceptual understanding. More realistic computational examples will be shown in coming lectures using the pymc3 and pystan packages.

 

In Bayesian statistics, we want to estimate the posterior distribution, but this is often intractable due to the high-dimensional integral in the denominator (marginal likelihood). A few other ideas we have encountered that are also relevant here are Monte Carlo integration with independent samples and the use of proposal distributions (e.g. rejection and importance sampling). As we have seen from the Monte Carlo integration lectures, we can approximate the posterior p(θ|X) if we can somehow draw many samples that come from the posterior distribution. With vanilla Monte Carlo integration, we need the samples to be independent draws from the posterior distribution, which is a problem if we do not actually know what the posterior distribution is (because we cannot integrate the marginal likelihood).

 

With MCMC, we draw samples from a (simple) proposal distribution so that each draw depends only on the state of the previous draw (i.e. the samples form a Markov chain). Under certain conditions, the Markov chain will have a unique stationary distribution. In addition, not all samples are used - instead we set up acceptance criteria for each draw based on comparing successive states with respect to a target distribution that ensure that the stationary distribution is the posterior distribution of interest. The nice thing is that this target distribution only needs to be proportional to the posterior distribution, which means we don’t need to evaluate the potentially intractable marginal likelihood, which is just a normalizing constant. We can find such a target distribution easily, since posterior ∝ likelihood × prior. After some time, the Markov chain of accepted draws will converge to the stationary distribution, and we can use those samples as (correlated) draws from the posterior distribution, and find functions of the posterior distribution in the same way as for vanilla Monte Carlo integration.

 

There are several flavors of MCMC, but the simplest to understand is the Metropolis-Hastings random walk algorithm, and we will start there.

---

Metropolis-Hastings random walk algorithm for estimating the bias of a coin

To carry out the Metropolis-Hastings algorithm, we need to draw random samples from the following distributions

def target(lik, prior, n, h, theta):
    if theta < 0 or theta > 1:
        return 0
    else:
        return lik(n, theta).pmf(h)*prior.pdf(theta)

n = 100
h = 61
a = 10
b = 10
lik = stats.binom
prior = stats.beta(a, b)
sigma = 0.3

naccept = 0
theta = 0.1
niters = 10000
samples = np.zeros(niters+1)
samples[0] = theta
for i in range(niters):
    theta_p = theta + stats.norm(0, sigma).rvs()
    rho = min(1, target(lik, prior, n, h, theta_p)/target(lik, prior, n, h, theta ))
    u = np.random.uniform()
    if u < rho:
        naccept += 1
        theta = theta_p
    samples[i+1] = theta
nmcmc = len(samples)//2
print("Efficiency = ", naccept/niters)

post = stats.beta(h+a, n-h+b)

plt.hist(samples[nmcmc:], 40, histtype='step', normed=True, linewidth=1, label='Prior');
plt.hist(prior.rvs(nmcmc), 40, histtype='step', normed=True, linewidth=1, label='Posterior');
plt.plot(thetas, post.pdf(thetas), c='red', linestyle='--', alpha=0.5, label='True posterior')
plt.xlim([0,1]);
plt.legend(loc='upper left')
pass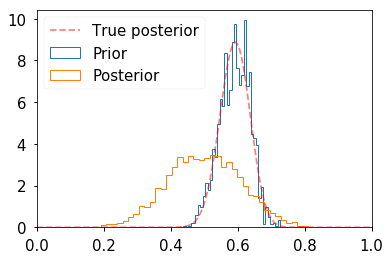

 

---

Assessing for convergence

Trace plots are often used to informally assess for stochastic convergence. Rigorous demonstration of convergence is an unsolved problem, but simple ideas such as running multiple chains and checking that they are converging to similar distributions are often employed in practice.

def mh_coin(niters, n, h, theta, lik, prior, sigma):
    samples = [theta]
    while len(samples) < niters:
        theta_p = theta + stats.norm(0, sigma).rvs()
        rho = min(1, target(lik, prior, n, h, theta_p)/target(lik, prior, n, h, theta ))
        u = np.random.uniform()
        if u < rho:
            theta = theta_p
        samples.append(theta)
    return samples

n = 100
h = 61
lik = stats.binom
prior = stats.beta(a, b)
sigma = 0.05
niters = 100

sampless = [mh_coin(niters, n, h, theta, lik, prior, sigma) for theta in np.arange(0.1, 1, 0.2)]

# Convergence of multiple chains

for samples in sampless:
    plt.plot(samples, '-o')
plt.xlim([0, niters])
plt.ylim([0, 1]);

---

Why does Metropolis-Hastings work?

There are two main ideas - first that the samples generated by MCMC constitute a Markov chain, and that this Markov chain has a unique stationary distribution that is always reached if we generate a very large number of samples. The second idea is to show that this stationary distribution is exactly the posterior distribution that we are looking for. We will only give the intuition here as a refresher.

One: There is a unique stationary state

Since possible transitions depend only on the current and the proposed values of θ, the successive values of θ in a Metropolis-Hastings sample constitute a Markov chain. Recall that for a Markov chain with a transition matrix T

π=πT

means that π is a stationary distribution. If it is possible to go from any state to any other state, then the matrix is irreducible. If in addition, it is not possible to get stuck in an oscillation, then the matrix is also aperiodic or mixing. For finite state spaces, irreducibility and aperiodicity guarantee the existence of a unique stationary state. For continuous state space, we need an additional property of positive recurrence - starting from any state, the expected time to come back to the original state must be finite. If we have all 3 properties of irreducibility, aperiodicity and positive recurrence, then there is a unique stationary distribution.

 

The term ergodic is a little confusing - most standard definitions take ergodicity to be equivalent to irreducibility, but often Bayesian texts take ergodicity to mean irreducibility, aperiodicity and positive recurrence, and we will follow the latter convention. For another intuitive perspective, the random walk Metropolis-Hasting algorithm is analogous to a diffusion process. Since all states are communicating (by design), eventually the system will settle into an equilibrium state. This is analogous to converging on the stationary state.

Two: The stationary state is the posterior probability distribution

We will consider the simplest possible scenario for an explicit calculation. Suppose we have a two-state system where the posterior probabilities are θ and 1−θ. Suppose θ<0.5. So we have the following picture with the Metropolis-Hastings algorithm:

---

Intuition

---

The Gibbs sampler

Suppose we have a vector parameters θ=(θ1,θ2,…,θk), and we want to estimate the joint posterior distribution p(θ|X). Suppose we can find and draw random samples from all the conditional distributions

 

With Gibbs sampling, the Markov chain is constructed by sampling from the conditional distribution for each parameter θi in turn, treating all other parameters as observed. When we have finished iterating over all parameters, we are said to have completed one cycle of the Gibbs sampler. Since hierarchical models are typically set up as products of conditional distributions, the Gibbs sampler is ubiquitous in Bayesian modeling. Where it is difficult to sample from a conditional distribution, we can sample using a Metropolis-Hastings algorithm instead - this is known as Metropolis within Gibbs.

 

Gibbs sampling is a type of random walk through parameter space, and hence can be thought of as a Metropolis-Hastings algorithm with a special proposal distribution. At each iteration in the cycle, we are drawing a proposal for a new value of a particular parameter, where the proposal distribution is the conditional posterior probability of that parameter. This means that the proposal move is always accepted. Hence, if we can draw samples from the conditional distributions, Gibbs sampling can be much more efficient than regular Metropolis-Hastings. More formally, we want to show that

 

Advantages of Gibbs sampling

• No need to tune proposal distribution
• Proposals are always accepted

Disadvantages of Gibbs sampling

• Need to be able to derive conditional probability distributions
• Need to be able to (cheaply) draw random samples from conditional probability distributions
• Can be very slow if parameters are correlated because you cannot take "diagonal" steps (draw picture to illustrate)

---

Motivating example

We will use the toy example, familiar from the EM lecture, of estimating the bias of two coins given sample pairs (z1,n1) and (z2,n2) where zi is the number of heads in ni tosses for coin i.

Setup

def bern(theta, z, N):
    """Bernoulli likelihood with N trials and z successes."""
    return np.clip(theta**z * (1-theta)**(N-z), 0, 1)

def bern2(theta1, theta2, z1, z2, N1, N2):
    """Bernoulli likelihood with N trials and z successes."""
    return bern(theta1, z1, N1) * bern(theta2, z2, N2)

def make_thetas(xmin, xmax, n):
    xs = np.linspace(xmin, xmax, n)
    widths =(xs[1:] - xs[:-1])/2.0
    thetas = xs[:-1]+ widths
    return thetas

from mpl_toolkits.mplot3d import Axes3D

def make_plots(X, Y, prior, likelihood, posterior, projection=None):
    fig, ax = plt.subplots(1,3, subplot_kw=dict(projection=projection, aspect='equal'), figsize=(12,3))
    if projection == '3d':
        ax[0].plot_surface(X, Y, prior, alpha=0.3, cmap=plt.cm.jet)
        ax[1].plot_surface(X, Y, likelihood, alpha=0.3, cmap=plt.cm.jet)
        ax[2].plot_surface(X, Y, posterior, alpha=0.3, cmap=plt.cm.jet)
        for ax_ in ax: ax_._axis3don = False
    else:
        ax[0].contour(X, Y, prior, cmap=plt.cm.jet)
        ax[1].contour(X, Y, likelihood, cmap=plt.cm.jet)
        ax[2].contour(X, Y, posterior, cmap=plt.cm.jet)
    ax[0].set_title('Prior')
    ax[1].set_title('Likelihood')
    ax[2].set_title('Posteior')
    plt.tight_layout()

thetas1 = make_thetas(0, 1, 101)
thetas2 = make_thetas(0, 1, 101)
X, Y = np.meshgrid(thetas1, thetas2)

Analytic solution

a = 2
b = 3

z1 = 11
N1 = 14
z2 = 7
N2 = 14

prior = stats.beta(a, b).pdf(X) * stats.beta(a, b).pdf(Y)
likelihood = bern2(X, Y, z1, z2, N1, N2)
posterior = stats.beta(a + z1, b + N1 - z1).pdf(X) * stats.beta(a + z2, b + N2 - z2).pdf(Y)
make_plots(X, Y, prior, likelihood, posterior)
make_plots(X, Y, prior, likelihood, posterior, projection='3d')

Grid approximation

def c2d(thetas1, thetas2, pdf):
    width1 = thetas1[1] - thetas1[0]
    width2 = thetas2[1] - thetas2[0]
    area = width1 * width2
    pmf = pdf * area
    pmf /= pmf.sum()
    return pmf

_prior = bern2(X, Y, 2, 8, 10, 10) + bern2(X, Y, 8, 2, 10, 10)
prior_grid = c2d(thetas1, thetas2, _prior)
_likelihood = bern2(X, Y, 1, 1, 2, 3)
posterior_grid = _likelihood * prior_grid
posterior_grid /= posterior_grid.sum()
make_plots(X, Y, prior_grid, likelihood, posterior_grid)
make_plots(X, Y, prior_grid, likelihood, posterior_grid, projection='3d')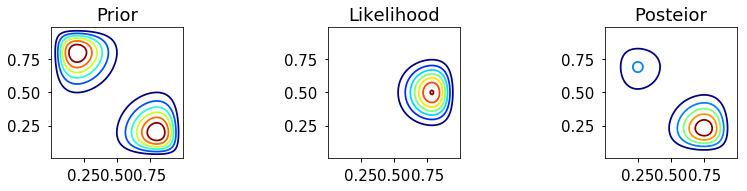

Metropolis

a = 2
b = 3

z1 = 11
N1 = 14
z2 = 7
N2 = 14

prior = lambda theta1, theta2: stats.beta(a, b).pdf(theta1) * stats.beta(a, b).pdf(theta2)
lik = partial(bern2, z1=z1, z2=z2, N1=N1, N2=N2)
target = lambda theta1, theta2: prior(theta1, theta2) * lik(theta1, theta2)

theta = np.array([0.5, 0.5])
niters = 10000
burnin = 500
sigma = np.diag([0.2,0.2])

thetas = np.zeros((niters-burnin, 2), np.float)
for i in range(niters):
    new_theta = stats.multivariate_normal(theta, sigma).rvs()
    p = min(target(*new_theta)/target(*theta), 1)
    if np.random.rand() < p:
        theta = new_theta
    if i >= burnin:
        thetas[i-burnin] = theta

kde = stats.gaussian_kde(thetas.T)
XY = np.vstack([X.ravel(), Y.ravel()])
posterior_metroplis = kde(XY).reshape(X.shape)
make_plots(X, Y, prior(X, Y), lik(X, Y), posterior_metroplis)
make_plots(X, Y, prior(X, Y), lik(X, Y), posterior_metroplis, projection='3d')

Gibbs

a = 2
b = 3

z1 = 11
N1 = 14
z2 = 7
N2 = 14

prior = lambda theta1, theta2: stats.beta(a, b).pdf(theta1) * stats.beta(a, b).pdf(theta2)
lik = partial(bern2, z1=z1, z2=z2, N1=N1, N2=N2)
target = lambda theta1, theta2: prior(theta1, theta2) * lik(theta1, theta2)

theta = np.array([0.5, 0.5])
niters = 10000
burnin = 500
sigma = np.diag([0.2,0.2])

thetas = np.zeros((niters-burnin,2), np.float)
for i in range(niters):
    theta = [stats.beta(a + z1, b + N1 - z1).rvs(), theta[1]]
    theta = [theta[0], stats.beta(a + z2, b + N2 - z2).rvs()]

    if i >= burnin:
        thetas[i-burnin] = theta

kde = stats.gaussian_kde(thetas.T)
XY = np.vstack([X.ravel(), Y.ravel()])
posterior_gibbs = kde(XY).reshape(X.shape)
make_plots(X, Y, prior(X, Y), lik(X, Y), posterior_gibbs)
make_plots(X, Y, prior(X, Y), lik(X, Y), posterior_gibbs, projection='3d')