Hamiltonian Monte Carlo

※ https://www.youtube.com/watch?v=a-wydhEuAm0&t=1182s

---

Idea

We want to generate more samples from the peaks of the probability density than in the tails of the density. We want to sample each location in exact proportion to its height so whilst we don't sample very often from the tails, in the shoulders we sample slightly more and in the head we sample even more than that.

 

For the clarity this is our shape of posterior density that we'd like to sample from.

 

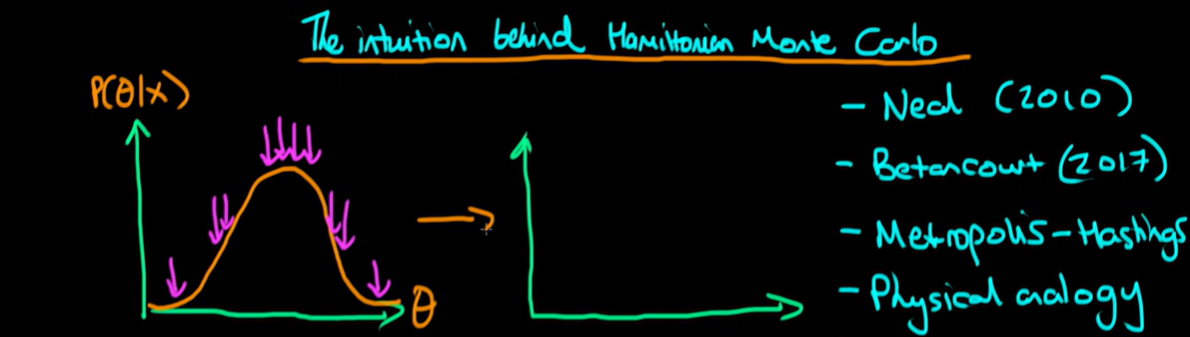
The idea with Hamiltonial Monte Carlo is essentially we flip this density. We flip it so that we are looking at something which looks like the exact kind of mirror image of the density we were looking at before.

 

Technically it's not just the mirror image. We also do something else to it we take the log of the posterior density. But for our purposes here just starting off we can think about it's just flipping this entity.

 

Then we do is imagine a fictitious particle which I call a sledge and imagine that this sledge is moving over this related terrain which is essentially the inverse of posterior space. And the idea is if we follow the path of this sledge over time then it will tend to go down towards the bottom of this landscape because it will just move under force of gravity and so because of that naturally our sledge will tend to visit those areas of lower density more often than those areas of high density in this related landscape so will tend to generate more samples from this location.

 

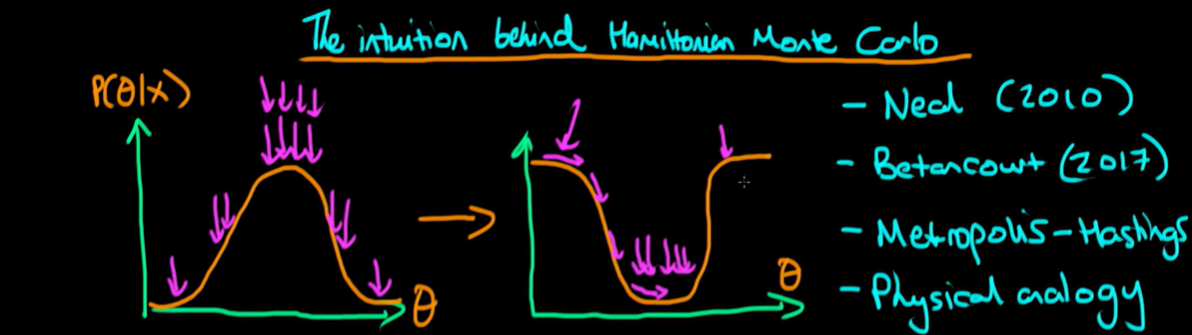
The bottom axis here is exactly the same between these two related spaces. What that means is if I generate lots of sample from down at the bottom of this right hand distribution, then that corresponds exactly to generating lots of samples from the peak of the posterior distribution.

 

The idea with Hamiltonian Monte Carlo is that we give our sledge a random kick now and again and that will allow it to also visit areas which are higher value in this right hand space here but they will visit these less frequently so it will also sample less frequently from the corresponding theta values in our posterior density.

 

That's essentially the whole physical analogy that underpins Hamiltonian Monte Carlo. It's about flipping the space and then imagining some fictitious particle which I call a sledge moving along this frictionless landscape.

 

So what we do in Hamiltonian Monte Carlo is we follow the path of this sledge and the eventual values that it traces out we use the samples from our posterior.

---

Statistical Mechanics

To motivate how statistical mechanics works I'm going to imagine that we have some sort of system which exists a discrete set of energy levels. For example this might be talking about the energy levels of a hydrogen atom.

 

Then the idea is that we have a number of these kind of energy levels and a particle can exist in any one of these discrete energy levels and the spacing between them need not be uniform indeed in hydrogen it's 1 over n squared where n corresponds to the subscript it.

 

And the idea here is that at the moment the particle as drawn it is existing in the lowest energy state. What can happen though is that if the particle absorbs heat from its surroundings then it can actually jump up to the next energy level so it might jump up to E1. Similarly, if it absorbs heat from E1, it can jump up to E2 but obviously that's less likely because then it would have had to have absorbed heat twice or a more bulky amount of heat in which case it would have jumped immediately from E0 to E2.

 

In statistical  mechanics we imagine that this system is thermal equilibrium with its surroundings. But even though it's a equilibrium with their surroundings it is constantly exchanging random amounts of heat with its surroundings. So it's constantly absorbing a random amount of heat from its surroundings and then constantly also emitting a random amount of heat.

 

So each time it absorbs heat it made jump up a level and each time it emits heat it may jump down an energy level. Because of this random behavior we don't know exactly what the state of the system is a given point of time.

 

The idea of statistical mechanics, the reason it's called statistical mechanics is that whilst we may not be able to figure out exactly what energy state the system is in at a given point in time, we can think about an infinity of equivalent systems and statistically we can think about the energy state of each of these infinity of systems which have all absorbed kind of random amounts of heat.

 

So one of the systems might be in the lowest energy level, the next one like also which will be the state for the most of these systems another one might exist in a slightly higher energy state because it's absorbed more heat.

 

And then the idea is what we can do is we can summarize the behavior across all of these different systems into something which is known as the canonical distribution which basically gives us associated with each of the energy levels a probability that the system is in that particular state.

 

So as I've said before the lowest energy level corresponds to having the highest probability that the particle is in that state. For the next energy level it is slightly less likely that we would get a particle in that energy state across all of our theoretic systems. Next one after that even less etc and we gonna get this decaying away.

 

You might ask what is actually the functional form which gives us this decay rate with energy. It turns out that the probability that the particle exists in any particular energy state is proportional to the exponent of minus the energy level. This kind of makes sense where E for the lowest energy level E0, E is the smallest value here and so we get the largest probability according to this formula.

 

For the next energy level which has got a slightly higher amounts of energy, e to the minus that is a smaller number and so we get this decaying away of the probability see with increases in the energy level. 

 

Now using a formula for the probability of the system is in any one particular energy level being equal to or proportional to e to the minus whatever the energy level is divided by T, we can try to figure out exactly what happens if we heat the system. 

 

If T is small then that means that the decay rate is going to be very very fast because we've then got essentially minus 1 over T which is going to be a large number so if the system is in a low temperature state then the majority of probability tends to be associated with the lowest energy levels.

 

Then if we heat the system, then T increases and 1 over T becomes smaller so the decay rate becomes less strong so what we get here now is we get probability which decays at a much slower rate so we get something like that and we're much more likely to find the system in a high energy state.

---

Hamiltonian Monte Carlo

In Hamiltonian Monte Carlo, what we do is we imagine that the system actually has an energy level and the system's energy depends on two things. 

 

It depends on the value of theta, the parameter and a property M which we create is the momentum of our thing which is sliding around on that analogous space.

 

Moreover the energy is the sum of two terms, the first is gravitational potential energy that only depends on the position of the particle and the other energy which gravitational potential energy is converted into is the kinetic energy of the particle, a function of the momentum. 

 

And we assume that the surface over which the particle is moving is frictionless which means that the sum of gravitational and kinetic energy is constant. 

 

Now we can use our result from statistical mechanics to try and work out what the probability of our system being in any one particular energy state is.

 

We know that the probability is going to be proportional to e to the minus the whatever energy level is, divided by T which is equal to using a formula above.

 

Now I want to discuss the particular functional form for our potential energy and for our kinetic energy.

 

But firstly before I do I want to make it clear theta (our parameter) is typically a vector. Similarly M is also a vector. We choose M to be of the same dimension as that of the theta. Because theta corresponds to the position in this multi-dimensional space and associated with each position direction, there should also be a corresponding momentum.

 

The kinetic energy of the particle is given by the momentum squared divided by 2 times its mass which exactly corresponds to the 1/2MV squres formula. In that formula, M corresponds to the mass and V is the velocity.

 

But to work out the total kinetic energy of the particle, we have to essentially sum over the kinetic energy of the particle in all of its D dimensions.

 

Then if we think about the functional form for U of theta, it turns out the convenient choice here is to choose U of theta to be minus the log of P of x given theta times P of theta. In other words, this is the likelihood and this is the prior so here by taking the log of all of it, we're taking the log of the unnormalized posterior.

 

And it's this space which I'll refer to the particle moving across and so I often refer to it as negative log posterior space.

 

So now I'm using our formula here except substituting in our explicit functional forms for the potential energy and kinetic energy, we can work out the probability that particle exists in any particular state.

 

And if we substitute in these forms we find that that's given by P of x given theta times P of theta, in other words the likelihood times the prior and the reason that the log has disappeared is because we've got e to the log and whenever you have e to the power log, essentially they cancel one another out and you've just left with the argument.

 

The other term that's left is just e to the minus M squated over two. And note that here as I'll do in what follows I've assumed that the temperature is one and that the mass of the particle is equal to one.

---

 

 

Then what we do is we actually notice that the functional form of the dependence of momentum is exactly the same as the functional form of a standard normal distribution.

 

And because we must be dealing with valid probability distributions here it actually must be a standard normal distribution so what it turns out is that this is equal to the product of unnormalized posterior times a standard normal PDF in the case where we've chosen the mass of the particle to be equal to one. If we chose the mass of the particle to be something else then we would change this one to whatever the value of the mass was.

 

You may be asking why is this actually helpful to us. We seem to have done a lot of mathematical kind of manipulation so what's the point of all of this.

 

Well the idea is that our joint density of theta (the thing we actually want) and the thing that we've created comes out as the product of two different terms.

 

There is a part which is due to theta and there is another part which is just use M. That's helpful because what it tells us is that the marginal distribution of theta is actually the posterior distribution.

 

Just to prove that to you if we were to integrate P of theta and M with respect to M in other words, we're marginalizing this joint density then that would amount to if we imagine the normalizing constant is Z that would amount to integrating the right hand side with respect to M for the first part of the right hand side doesn't depend on M so we can take that outside of the integral and then the second part is the integral of a normal density with respect to M and a normal density is a valid probability density.

 

Hence this next term here is one and then we get on the left hand side yet P of theta is just equal to one of Z, P X of theta given theta times P of theta, in other words our marginal density is our posterior density.

 

So the idea is in practice we don't do this integration. But it turns out what we can do instead is we can sample from the joint distribution of theta and M and then we can essentially just throw away all of our M samples and the marginal distribution of theta will turn out to be samples from our posterior distribution.

---

You may still be thinking well that's all fine but how do we actually generate samples of theta and M and how do we generate proposals in particular for theta and M?

 

Well, the idea is quite simple really. We can generate proposals for M quite simply by just sampling from its normal density. We can independently sample from that. So we sample a value of M from a standard  normal distribution if we've chosen the mass of the particle to be equal to 1.

 

Then the clever part of this is that we then solve for the path of the particle assuming that it's got a gravitational potential energy given by U of theta and a kinetic energy given by K of M.

 

 

And Newtonian dynamics tells you how to use these two quantities to solve exactly for the path of the particle over time.

 

So the idea is that we would ideally solve for the continuous part of particle for a set period of time in each iteration of the algorithm we used the same amount of time to follow our sledge form. 

 

 

In most interesting circumstances we cannot exactly solve for the path of the particle so ultimately what we end up doing is we discretizing its path and the idea is if we choose these steps of our discretizing algorithm to be small enough then hopefully the approximation is reasonably good and in particular the most common algorithm which is used here is known as the leap frog algorithm.

 

And the leap frog algorithm has a particular property which is known as being a symplectic integrator which essentially means that we can contain the errors of this discretizing process.

 

 

In summary what we're doing is we're solving for the path of the particle over time and this is deterministic given our current value of theta and the value of M that we sample and what that then gives us is a proposed value of theta and proposed value of our momentum.

---

 

Then what we do is we calculate a metropolis ratio but using our joint distribution of theta and M that we worked our before. So now we calculate a ratio r which is equal to P of X given the proposed value of theta star times P of theta start times the value of a normal density at the proposed value of M divided through by P of X given theta times P of theta times our normal density evaluated at the original value of M that we proposed. 

 

Those that are keen-eyed amongst you will know that this formula as I've written it down here is exactly the same as the metropolis formula but we're assuming that we've got a joint density which is also includes this normal term here. 

 

However you'll also know that this isn't quite satisfactory as it stands because I haven't dealt with the potential asymmetry between proposals from Theta to M to those going in the opposite direction. So actually what we need to include as well is a Hastings term which is the probability that we propose theta and M assuming we start from theta star and M star divided through by the probability that we've proposed the theta star and M star given that we're starting at theta and M.

 

And this is just exactly the part of the formula that you add in the metropolis Hastings rule and it's dealing with the asymmetry of proposals.

---

 

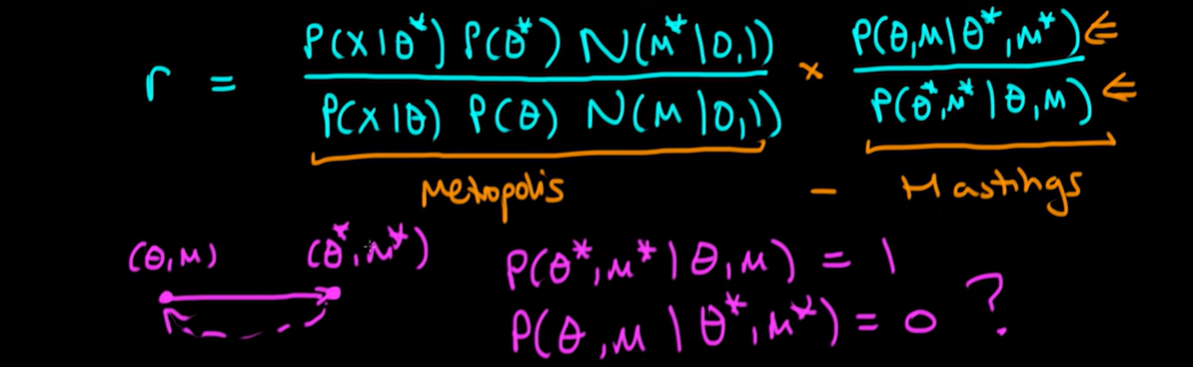
But what exactly do each of these terms look like because isn't the path deterministic. Indeed it is. If we start at a particular value of theta and a particular value of M, then the path of the particle deteministically leads to theta star and M star.

 

What does that means we can write the probability that proposed theta star and M star given that we start at theta and M is equal to 1 but the probability that we start at theta star and M star and we move back in the opposite direction so that after the same amount of time we exactly end up at theta and M is going to be 0 will be very very lucky if that were the case that we have this entire symmetry between our proposed value of theta and M and the values that we end up with at the end of running our particle. 

 

So as we can't currently have it the probability of proposing theta and M given theta star and M star actually equal zero so we've got some sort of problem here because if we insert these terms into our ratio, then we always get the value of r which is equal to zero in other words we will never accept the proposals.

 

 

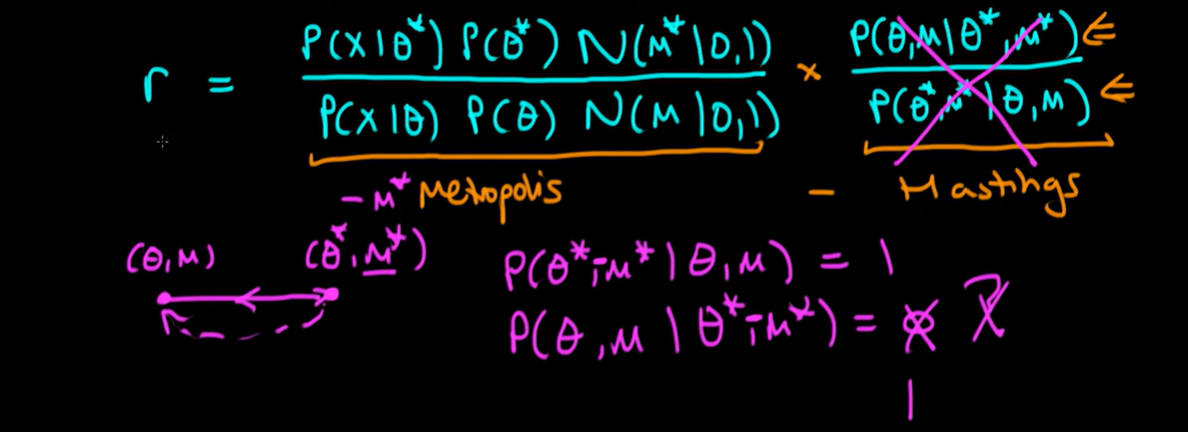
The way that we fix this problem is by taking the value of M that we proposed this sort of end of our simulation and just timesing it by minus one so instead here we get minus M star and then that fixes everything.

 

Because still the way in which we are doing our proposals works because now we're just always going to flip the value of M star so the probability that we start a theta and M and go to theta star and then minus M star is equal to one and similarly if we start at theta star and M star and I'm considering a negative value of the momentum then that's going to be exactly the amount that takes us back in the opposite direction and will mean that we'll end up exactly where we started in the beginning and so now the second term doesn't equal to zero it actually equals one so why does this help us the idea is that we can cancel this whole horrible right-hand side term in our ratio. I should technically negate the M star in the other part of the ratio but since for a normal density it's symmetric about zero this doesn't make any difference so I'm just gonna leave it as it is.

---

 

Then once we've got our ratio of all, all we do is we proceed exactly as we do in metropolis if r is greater than some uniformly distributed number between zero and one, some random sample from a uniform distribution between zero and one, then we accept the proposed values of theta and M to be our next samples from our distribution, if that is not true, then the value of theta and M for our next iteration just remain as they were at the beginning so we just start off at theta and the initial value of M that we proposed.

 

So essentially this algorithm is exactly the same as a metropolis algorithm except when we're considering the joint space of theta and M. And the way in which we're doing proposals isn't the same as the random walk metropolis algorithm, we are solving for the path of the particle using deterministic equations Newton's equations of motion.

 

I now want to illustrate how this process works for a particular example and the example that I'm going to use here is assuming that our posterior distribution has a kind of bimodal form that looks something like this. So this is the shape of the posterior but what I what to do is I want to show you the path of our particle in our joint space P of theta and M. So to get our joint space all I do is I multiply the posterior by a normal density which represents the M part of our joint and then I get a two dimensional distribution which are show in a minute but essentially the point is any slice through this 2D distribution for a particular value of M, just will give me back the original shape of the posterior.

---

 

So here I'm just graphically representing this so on the left hand I have a 3D representation of our joint density and so we have our position theta or our particle and its momentum along the other axis and so you can see as I rotate this to the sort of theta plane that we do just get back our bimodal shape of our posterior if we just look for a particular slice of M. 

 

Another way of representing this density is shown here on the right which is just a contour plot. I now want to show you the path of our particle over time in this joint space so I've started the particle so that it's halfway between these two modes and I've sampled a value of M so that gives me a starting point in this joint space then if we follow the path of this particle over time we get a kind of arc which I'm showing here by this green arrow it's green because we ultimately end up accepting this proposal but you can see that a particle is following some sort of smooth motion here which is quite close to circular motion and it's quite close to circular motion because essentially I've used the sum of two normals here but that doesn't matter too much but you can see that we're sort of solving for the path of our particle over time.

 

 

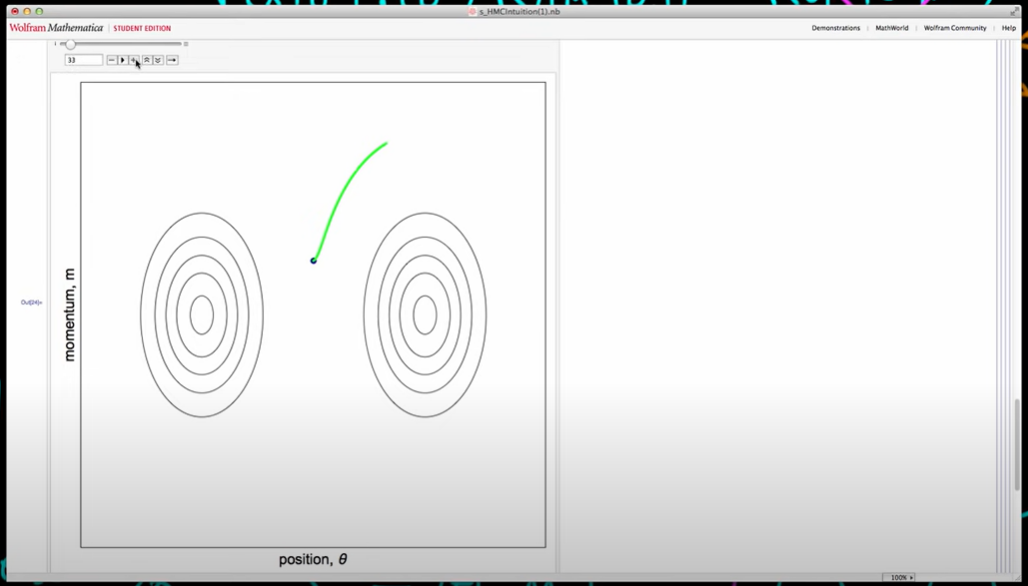
And then as we continue to solve for its path in both momentum and position space eventually we get to the point the end of our algorithm after we've simulated this motion for L the screen steps where we end up at this sort of position which is given by sort of wherever this intersects this axis here but then what we do we flip the sign of momentum and so we jump down to this position here and it turns out fiven our ratio r that we can calculate we actually accept this proposal so this forms our next sample from our joint distribution and then the idea is our point in this space jumps up because then we sample a fresh value of M so that's why we're somewhere near the middle now and that axe is our initial value of M which we use to solve for the path of the particle in the next iteration.

 

And the idea is that we can continue this process so in each step of the algorithm we sample a new value of M and then what we do is we solve for the motion of the particle using Newton's equations of motion essentially we use approximate ways of integrating those equations of motion and you actually saw that there one of the times we actually rejected the proposal because I showed the path in orange there but you can see that each time at the end of solving for the path of the particle, we flipped the sign of the momentum, so the momentum here below this at a point here is negative then it becomes positive and again you just saw that we rejected a proposed step and it actually turns out the reasons for rejecting a proposed step is due to the approximation error in solving for our path of our particle over time.

 

But you can see here is that we're starting to build up a range of samples which if you look in the theta dimension, we start to get a lot of samples towards the modes of each of these distributions. So the marginal distribution for theta if we were to run this much much longer, turns out to be the shape of the posterior that we would like to obtain and similarly if we were to look in the momentum dimension then eventually the samples for momentum actually fall the normal distribution that we want to be sampling from that. 

---

However there is another way that we can kind of view this process which is that every time we propose a new value of M essentially that changes our energy level and so each of these contours corresponds to lines of constant energy and so every time we propose a new value of M we jump up or down to a new energy state and so our ability to efficiently explore this space actually comes down to whether or not we are proposing reasonable values of energy which encompasses the entire range of energies which are represented by this joint distribution so now I want to show the process of running Hamiltonian Monte Carlo on this particular example for a bit longer so here above the contour plot I'm showing the desired marginal distribution of which corresponds to our posterior here and then to the right hand side I showed the desired marginal distribution which corresponds to our normal one distribution for our momentum. 

 

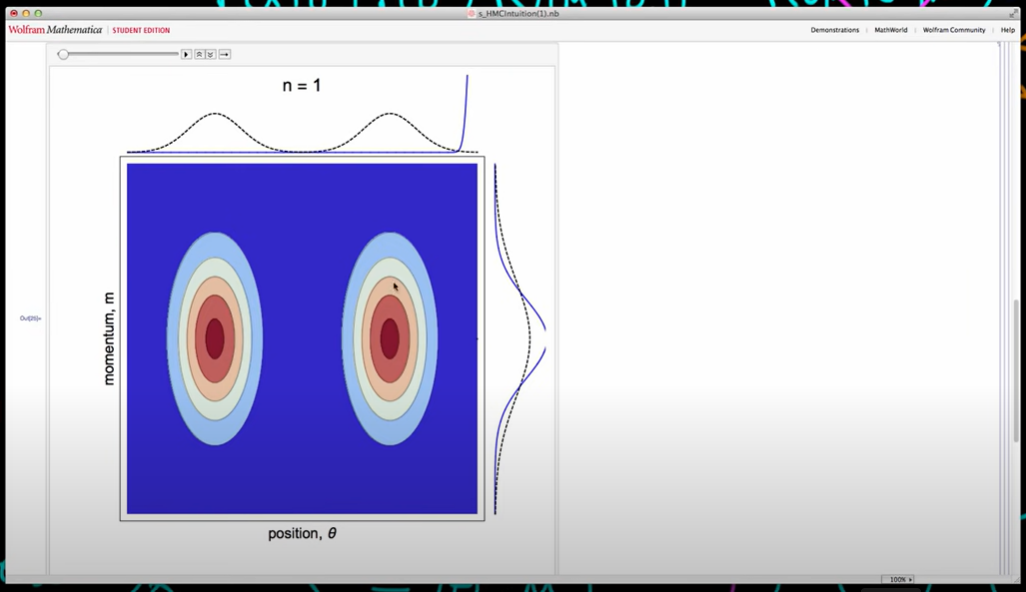
We can see and we can imagine that if we were to run this for a bit longer then we would eventually get convergence to our posterior distribution or joint distribution here and so we can see after 20,000 samples that we've actually got pretty close to our posterior distribution. It's still not that close because its difficult distribution HMC want to sample from it doesn't deal well with bimodal distributions. But it doing pretty well much bettern thatn metropolis Hastings would do typically.

 

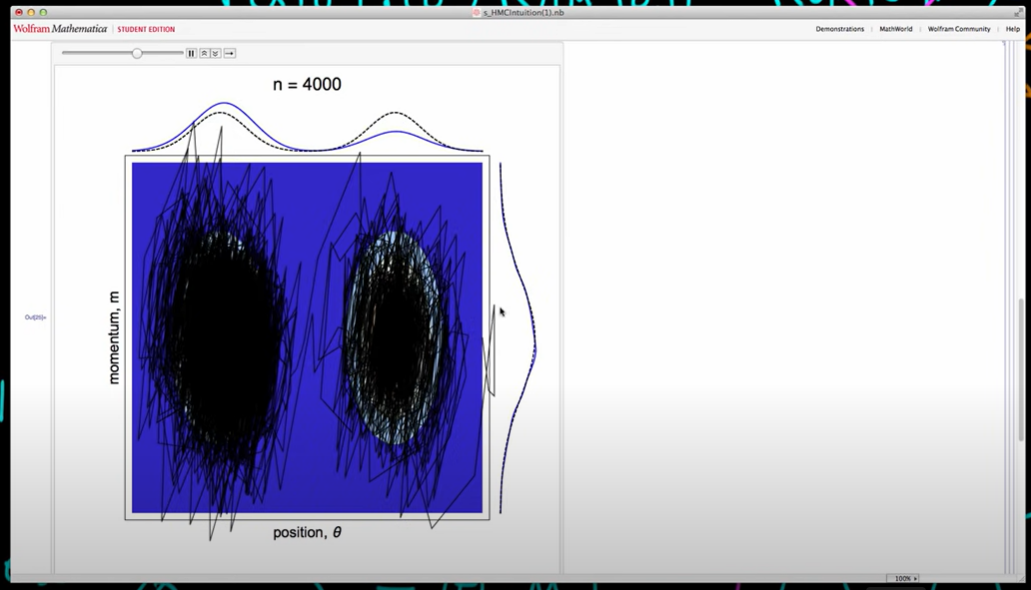
And we can see that we've converged very closely to the desired momentum distribution.

---

So in summary Hamiltonian Monte Carlo is a variant of the Metropolis-Hastings algorithm and the way in which it differs from standard Metropolis-Hastings is, by using a physical analogy to generate proposals for theta and the physical analogy that helps us is by imagining the path of a fictitious particle on a space which is related to posterior space which I call "negative log posterior space" and because that space is essentially the inverse of posterior space then we tend to flow to regions of low negative log posterior, which corresponds to high values of posterior so we tend to sample more from the modes which is exactly what we would want to do.