[CVAE 1] Learning Structured Output Representation using Deep Conditional Generative Models

※ https://proceedings.neurips.cc/paper_files/paper/2015/file/8d55a249e6baa5c06772297520da2051-Paper.pdf

---

※ Structured prediction

In standard Machine Learning setting the output is a scalar quantity which is fine for most of the real world problems, but there are some problems where the expected output of Machine Learning model is a complex structure like tree, graph, image etc. To apply Machine Learning to such cases Structured prediction is used where the output can be complex structure instead of a scalar.

 

To clarify more on this, consider you want to apply Machine Learning to denoise an image. The training samples will be image pairs with input as noisy image and output as clean version of this image. In this setting the Machine Learning model is expected to learn a mapping from noisy image to clean image i.e the output in this case is an image. A similar kind of problem could be denoising speech signals. The problem setting is similar to the image case.

 

Structured prediction is a machine learning technique used for predicting structured objects, such as sequences, trees, or graphs, where the output is not just a single label or value, but a complex structure. This technique is commonly used in natural language processing, speech recognition, and computer vision, where the output is often a sequence of words, a parse tree, or a spatial arrangement of objects. Structured prediction methods aim to capture dependencies between the output components and make joint predictions that respect these dependencies. This can lead to more accurate predictions compared to making independent predictions for each component.

 

구조화된 예측: 출력 변수가 상호 의존적이거나 제약되는 분류 또는 회귀 문제를 해결하기 위한 프레임워크. 이러한 종속성과 제약 조건은 문제 영역에서 순차적, 공간적 또는 조합적 구조를 반영하며 이러한 상호 작용을 캡처하는 것은 입출력 종속성을 캡처하는 것만큼 중요.

 

분류 문제에서는 여러 입력값들이 한 개의 값으로 매핑되지만, "구조화된 예측" 문제에서는 하나의 입력값으로 가능한 다양한 출력값을 매핑. 일부 입력 데이터 x가 주어진 경우, 해당 데이터와 관련된 최상의 구조를 찾는 게 목표. 이는 문제를 해결하기 위해 일종의 검색이 필요하다는 의미.

 

논문에서 제안하는 conditional variational auto-encoder는 기존 VAE 구조를 지도학습이 가능하도록 인코더와 디코더에 정답 레이블 y를 추가한 형태로 변형.

---

Abstract

Supervised deep learning has been successfully applied to many recognition problems. Although it can approximate a complex many-to-one function well when a large amount of training data is provided, it is still challenging to model complex structured output representations that effectively perform probabilistic inference and make diverse predictions.

 

In this work, we develop a deep conditional generative model for structured output prediction using Gaussian latent variables. The model is trained efficiently in the framework of stochastic gradient variational Bayes, and allows for fast prediction using stochastic feed-forward inference.

 

In addition, we provide novel strategies to build robust structured prediction algorithms, such as input noise-injection and multi-scale prediction objective at training. In experiments, we demonstrate the effectiveness of our proposed algorithm in comparison to the deterministic deep neural network counterparts in generating diverse but realistic structured output predictions using stochastic inference.

 

Furthermore, the proposed training methods are complimentary, which leads to strong pixel-level object segmentation and semantic labeling performance on Caltech-UCSD Birds 200 and subset of Labeled Faces in the Wild dataset.

---

1. Introduction

In structured output prediction, it is important to learn a model that can perform probabilistic inference and make diverse predictions. This is because we are not simply modeling a many-to-one function as in classification tasks, but we may need to model a mapping from single input to many possible outputs. Recently, the convolutional neural networks (CNNs) have been greatly successful for large-scale image classification tasks [17, 30, 27] and have also demonstrated promising results for structured prediction tasks (e.g., [4, 23, 22]). However, the CNNs are not suitable in modeling a distribution with multiple modes [32].

 

To address this problem, we propose novel deep conditional generative models (CGMs) for output representation learning and structured prediction. In other words, we model the distribution of highdimensional output space as a generative model conditioned on the input observation. Building upon recent development in variational inference and learning of directed graphical models [16, 24, 15], we propose a conditional variational auto-encoder (CVAE). The CVAE is a conditional directed graphical model whose input observations modulate the prior on Gaussian latent variables that generate the outputs. It is trained to maximize the conditional log-likelihood, and we formulate the variational learning objective of the CVAE in the framework of stochastic gradient variational Bayes (SGVB) [16]. In addition, we introduce several strategies, such as input noise-injection and multi-scale prediction training methods, to build a more robust prediction model.

 

In experiments, we demonstrate the effectiveness of our proposed algorithm in comparison to the deterministic neural network counterparts in generating diverse but realistic output predictions using stochastic inference. We demonstrate the importance of stochastic neurons in modeling the structured output when the input data is partially provided. Furthermore, we show that the proposed training schemes are complimentary, leading to strong pixel-level object segmentation and labeling performance on Caltech-UCSD Birds 200 and the subset of Labeled Faces in the Wild dataset.

 

In summary, the contribution of the paper is as follows:

• We propose CVAE and its variants that are trainable efficiently in the SGVB framework, and introduce novel strategies to enhance robustness of the models for structured prediction.
• We demonstrate the effectiveness of our proposed algorithm with Gaussian stochastic neurons in modeling multi-modal distribution of structured output variables.
• We achieve strong semantic object segmentation performance on CUB and LFW datasets.

The paper is organized as follows. We first review related work in Section 2. We provide preliminaries in Section 3 and develop our deep conditional generative model in Section 4. In Section 5, we evaluate our proposed models and report experimental results. Section 6 concludes the paper.

---

2. Related work

Since the recent success of supervised deep learning on large-scale visual recognition [17, 30, 27], there have been many approaches to tackle mid-level computer vision tasks, such as object detection [6, 26, 31, 9] and semantic segmentation [4, 3, 23, 22], using supervised deep learning techniques. Our work falls into this category of research in developing advanced algorithms for structured output prediction, but we incorporate the stochastic neurons to model the conditional distributions of complex output representation whose distribution possibly has multiple modes. In this sense, our work shares a similar motivation to the recent work on image segmentation tasks using hybrid models of CRF and Boltzmann machine [13, 21, 37]. Compared to these, our proposed model is an end-to-end system for segmentation using convolutional architecture and achieves significantly improved performance on challenging benchmark tasks.

 

Along with the recent breakthroughs in supervised deep learning methods, there has been a progress in deep generative models, such as deep belief networks [10, 20] and deep Boltzmann machines [25]. Recently, the advances in inference and learning algorithms for various deep generative models significantly enhanced this line of research [2, 7, 8, 18]. In particular, the variational learning framework of deep directed graphical model with Gaussian latent variables (e.g., variational autoencoder [16, 15] and deep latent Gaussian models [24]) has been recently developed. Using the variational lower bound of the log-likelihood as the training objective and the reparameterization trick, these models can be easily trained via stochastic optimization. Our model builds upon this framework, but we focus on modeling the conditional distribution of output variables for structured prediction problems. Here, the main goal is not only to model the complex output representation but also to make a discriminative prediction. In addition, our model can effectively handle large-sized images by exploiting the convolutional architecture.

 

The stochastic feed-forward neural network (SFNN) [32] is a conditional directed graphical model with a combination of real-valued deterministic neurons and the binary stochastic neurons. The SFNN is trained using the Monte Carlo variant of generalized EM by drawing multiple samples from the feed-forward proposal distribution and weighing them differently with importance weights. Although our proposed Gaussian stochastic neural network (which will be described in Section 4.2) looks similar on surface, there are practical advantages in optimization of using Gaussian latent variables over the binary stochastic neurons. In addition, thanks to the recognition model used in our framework, it is sufficient to draw only a few samples during training, which is critical in training very deep convolutional networks.

---

3. Preliminary: Variational Auto-encoder

The variational auto-encoder (VAE) [16, 24] is a directed graphical model with certain types of latent variables, such as Gaussian latent variables. A generative process of the VAE is as follows: a set of latent variable z is generated from the prior distribution pθ(z) and the data x is generated by the generative distribution pθ(x|z) conditioned on z: z ∼ pθ(z), x ∼ pθ(x|z).

 

In general, parameter estimation of directed graphical models is often challenging due to intractable posterior inference. However, the parameters of the VAE can be estimated efficiently in the stochastic gradient variational Bayes (SGVB) [16] framework, where the variational lower bound of the log-likelihood is used as a surrogate objective function. The variational lower bound is written as:

 

In this framework, a proposal distribution qφ(z|x), which is also known as a “recognition” model, is introduced to approximate the true posterior pθ(z|x). The multilayer perceptrons (MLPs) are used to model the recognition and the generation models. Assuming Gaussian latent variables, the first term of Equation (2) can be marginalized, while the second term is not. Instead, the second term can be approximated by drawing samples z (l) (l = 1, ..., L) by the recognition distribution qφ(z|x), and the empirical objective of the VAE with Gaussian latent variables is written as follows:

 

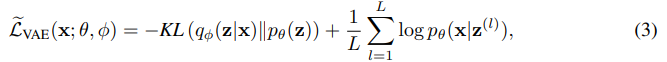
where

 

Note that the recognition distribution qφ(z|x) is reparameterized with a deterministic, differentiable function gφ(·, ·), whose arguments are data x and the noise variable e. This trick allows error backpropagation through the Gaussian latent variables, which is essential in VAE training as it is composed of multiple MLPs for recognition and generation models. As a result, the VAE can be trained efficiently using stochastic gradient descent (SGD).

---

4. Deep Conditional Generative Models for Structured Output Prediction

 

As illustrated in Figure 1, there are three types of variables in a deep conditional generative model (CGM): input variables x, output variables y, and latent variables z. The conditional generative process of the model is given in Figure 1(b) as follows: for given observation x, z is drawn from the prior distribution pθ(z|x), and the output y is generated from the distribution pθ(y|x, z). Compared to the baseline CNN (Figure 1(a)), the latent variables z allow for modeling multiple modes in conditional distribution of output variables y given input x, making the proposed CGM suitable for modeling one-to-many mapping. The prior of the latent variables z is modulated by the input x in our formulation; however, the constraint can be easily relaxed to make the latent variables statistically independent of input variables, i.e., pθ(z|x) = pθ(z) [15].

 

Deep CGMs are trained to maximize the conditional log-likelihood. Often the objective function is intractable, and we apply the SGVB framework to train the model. The variational lower bound of the model is written as follows (complete derivation can be found in the supplementary material):

 

and the empirical lower bound is written as:

 

where z (l) = gφ(x, y, e(l)), e(l) ∼ N (0, I) and L is the number of samples. We call this model conditional variational auto-encoder (CVAE). The CVAE is composed of multiple MLPs, such as recognition network qφ(z|x, y), (conditional) prior network pθ(z|x), and generation network pθ(y|x, z). In designing the network architecture, we build the network components of the CVAE on top of the baseline CNN. Specifically, as shown in Figure 1(d), not only the direct input x, but also the initial guess yˆ made by the CNN are fed into the prior network. Such a recurrent connection has been applied for structured output prediction problems [23, 13, 28] to sequentially update the prediction by revising the previous guess while effectively deepening the convolutional network. We also found that a recurrent connection, even one iteration, showed significant performance improvement. Details about network architectures can be found in the supplementary material.

---

4.1 Output inference and estimation of the conditional likelihood

Once the model parameters are learned, we can make a prediction of an output y from an input x by following the generative process of the CGM. To evaluate the model on structured output prediction tasks (i.e., in testing time), we can measure a prediction accuracy by performing a deterministic inference without sampling z, i.e., y* = arg max y pθ(y|x, z*), z* = E[z|x].

 

Another way to evaluate the CGMs is to compare the conditional likelihoods of the test data. A straightforward approach is to draw samples z’s using the prior network and take the average of the likelihoods. We call this method the Monte Carlo (MC) sampling:

It usually requires a large number of samples for the Monte Carlo log-likelihood estimation to be accurate. Alternatively, we use the importance sampling to estimate the conditional likelihoods [24]:

---

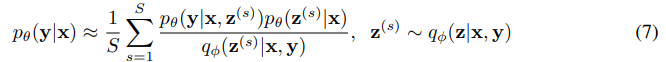
4.2 Learning to predict structured output

Although the SGVB learning framework has shown to be effective in training deep generative models [16, 24], the conditional auto-encoding of output variables at training may not be optimal to make a prediction at testing in deep CGMs. In other words, the CVAE uses the recognition network qφ(z|x, y) at training, but it uses the prior network pθ(z|x) at testing to draw samples z’s and make an output prediction. Since y is given as an input for the recognition network, the objective at training can be viewed as a reconstruction of y, which is an easier task than prediction. The negative KL divergence term in Equation (5) tries to close the gap between two pipelines, and one could consider allocating more weights on the negative KL term of an objective function to mitigate the discrepancy in encoding of latent variables at training and testing, i.e., −(1 + β)KL (qφ(z|x, y)||pθ(z|x)) with β ≥ 0. However, we found this approach ineffective in our experiments.

 

Instead, we propose e to train the networks in a way that the prediction pipelines at training and testing are consistent. This can be done by setting the recognition network the same as the prior network, i.e., qφ(z|x, y) = pθ(z|x), and we get the following objective function:

We call this model Gaussian stochastic neural network (GSNN).3 Note that the GSNN can be derived from the CVAE by setting the recognition network and the prior network equal. Therefore, the learning tricks, such as reparameterization trick, of the CVAE can be used to train the GSNN. Similarly, the inference (at testing) and the conditional likelihood estimation are the same as those of CVAE. Finally, we combine the objective functions of two models to obtain a hybrid objective:

where α balances the two objectives. Note that when α = 1, we recover the CVAE objective; when α = 0, the trained model will be simply a GSNN without the recognition network.

---

4.3 CVAE for image segmentation and labeling

Semantic segmentation [5, 23, 6] is an important structured output prediction task. In this section, we provide strategies to train a robust prediction model for semantic segmentation problems. Specifically, to learn a high-capacity neural network that can be generalized well to unseen data, we propose to train the network with 1) multi-scale prediction objective and 2) structured input noise.

---

5. Experiments

We demonstrate the effectiveness of our approach in modeling the distribution of the structured output variables. For the proof of concept, we create an artificial experimental setting for structured output prediction using MNIST database [19]. Then, we evaluate the proposed CVAE models on several benchmark datasets for visual object segmentation and labeling, such as Caltech-UCSD Birds (CUB) [36] and Labeled Faces in the Wild (LFW) [12]. Our implementation is based on MatConvNet [33], a MATLAB toolbox for convolutional neural networks, and Adam [14] for adaptive learning rate scheduling algorithm of SGD optimization.

---

6. Conclusion

Modeling multi-modal distribution of the structured output variables is an important research question to achieve good performance on structured output prediction problems. In this work, we proposed stochastic neural networks for structured output prediction based on the conditional deep generative model with Gaussian latent variables. The proposed model is scalable and efficient in inference and learning. We demonstrated the importance of probabilistic inference when the distribution of output space has multiple modes, and showed strong performance in terms of segmentation accuracy, estimation of conditional log-likelihood, and visualization of generated samples.