[CVAE 2] Semi-supervised Learning with Deep Generative Models

※ https://arxiv.org/pdf/1406.5298.pdf

---

Abstract

The ever-increasing size of modern data sets combined with the difficulty of obtaining label information has made semi-supervised learning one of the problems of significant practical importance in modern data analysis. We revisit the approach to semi-supervised learning with generative models and develop new models that allow for effective generalisation from small labelled data sets to large unlabelled ones. Generative approaches have thus far been either inflexible, inefficient or non-scalable. We show that deep generative models and approximate Bayesian inferernce exploiting recent advances in variational methods can be used to provide significant improvements, making generative approaches highly competitive for semi-supervised learning.

 

레이블 정보를 얻는 어려움과 결합된 최신 데이터 세트의 크기가 계속 증가함에 따라 반지도 학습은 현대 데이터 분석에서 실질적으로 중요한 문제 중 하나가 되었습니다. 생성 모델을 사용하여 준지도 학습에 대한 접근 방식을 다시 검토하고 작은 레이블이 지정된 데이터 세트에서 레이블이 없는 큰 데이터 세트에 이르기까지 효과적인 일반화를 허용하는 새로운 모델을 개발합니다. 지금까지 생성 접근 방식은 유연하지 않거나 비효율적이거나 확장 불가능했습니다. 우리는 변형 방법의 최근 발전을 활용하는 심층 생성 모델과 근사 베이지안 추론을 사용하여 상당한 개선을 제공하여 생성 접근 방식을 반지도 학습에 대해 매우 경쟁력 있게 만들 수 있음을 보여줍니다.

---

1. Introduction

Semi-supervised learning considers the problem of classification when only a small subset of the observations have corresponding class labels. Such problems are of immense practical interest in a wide range of applications, including image search (Fergus et al., 2009), genomics (Shi and Zhang, 2011), natural language parsing (Liang, 2005), and speech analysis (Liu and Kirchhoff, 2013), where unlabelled data is abundant, but obtaining class labels is expensive or impossible to obtain for the entire data set. The question that is then asked is: how can properties of the data be used to improve decision boundaries and to allow for classification that is more accurate than that based on classifiers constructed using the labelled data alone. In this paper we answer this question by developing probabilistic models for inductive and transductive semi-supervised learning by utilising an explicit model of the data density, building upon recent advances in deep generative models and scalable variational inference (Kingma and Welling, 2014; Rezende et al., 2014).

 

Amongst existing approaches, the simplest algorithm for semi-supervised learning is based on a self-training scheme (Rosenberg et al., 2005) where the the model is bootstrapped with additional labelled data obtained from its own highly confident predictions; this process being repeated until some termination condition is reached. These methods are heuristic and prone to error since they can reinforce poor predictions. Transductive SVMs (TSVM) (Joachims, 1999) extend SVMs with the aim of max-margin classification while ensuring that there are as few unlabelled observations near the margin as possible. These approaches have difficulty extending to large amounts of unlabelled data, and efficient optimisation in this setting is still an open problem. Graph-based methods are amongst the most popular and aim to construct a graph connecting similar observations; label information propagates through the graph from labelled to unlabelled nodes by finding the minimum energy (MAP) configuration (Blum et al., 2004; Zhu et al., 2003). Graph-based approaches are sensitive to the graph structure and require eigen-analysis of the graph Laplacian, which limits the scale to which these methods can be applied – though efficient spectral methods are now available (Fergus et al., 2009). Neural network-based approaches combine unsupervised and supervised learning by training feed-forward classifiers with an additional penalty from an auto-encoder or other unsupervised embedding of the data (Ranzato and Szummer, 2008; Weston et al., 2012). The Manifold Tangent Classifier (MTC) (Rifai et al., 2011) trains contrastive auto-encoders (CAEs) to learn the manifold on which the data lies, followed by an instance of TangentProp to train a classifier that is approximately invariant to local perturbations along the manifold. The idea of manifold learning using graph-based methods has most recently been combined with kernel (SVM) methods in the Atlas RBF model (Pitelis et al., 2014) and provides amongst most competitive performance currently available.

 

In this paper, we instead, choose to exploit the power of generative models, which recognise the semi-supervised learning problem as a specialised missing data imputation task for the classification problem. Existing generative approaches based on models such as Gaussian mixture or hidden Markov models (Zhu, 2006), have not been very successful due to the need for a large number of mixtures components or states to perform well. More recent solutions have used non-parametric density models, either based on trees (Kemp et al., 2003) or Gaussian processes (Adams and Ghahramani, 2009), but scalability and accurate inference for these approaches is still lacking. Variational approximations for semi-supervised clustering have also been explored previously (Li et al., 2009; Wang et al., 2009).

 

Thus, while a small set of generative approaches have been previously explored, a generalised and scalable probabilistic approach for semi-supervised learning is still lacking. It is this gap that we address through the following contributions:

• We describe a new framework for semi-supervised learning with generative models, employing rich parametric density estimators formed by the fusion of probabilistic modelling and deep neural networks.
• We show for the first time how variational inference can be brought to bear upon the problem of semi-supervised classification. In particular, we develop a stochastic variational inference algorithm that allows for joint optimisation of both model and variational parameters, and that is scalable to large datasets.
• We demonstrate the performance of our approach on a number of data sets providing state-of-the-art results on benchmark problems.
• We show qualitatively generative semi-supervised models learn to separate the data classes (content types) from the intra-class variabilities (styles), allowing in a very straightforward fashion to simulate analogies of images on a variety of datasets.

준지도 학습은 관측치의 작은 하위 집합에만 해당 클래스 레이블이 있는 경우 분류 문제를 고려합니다. 이러한 문제는 이미지 검색 (Fergus et al., 2009), 유전체학 (Shi and Zhang, 2011), 자연어 파싱 (Liang, 2005), 음성 분석 (Liu 및 Kirchhoff, 2013), 여기서 레이블이 지정되지 않은 데이터는 풍부하지만 클래스 레이블을 얻는 것은 비용이 많이 들거나 전체 데이터 세트에 대해 얻을 수 없습니다. 그런 다음 질문은 데이터 속성을 사용하여 결정 경계를 개선하고 레이블이 지정된 데이터만 사용하여 구성된 분류자를 기반으로 하는 분류 기준보다 더 정확한 분류를 허용하는 방법입니다. 이 논문에서 우리는 데이터 밀도의 명시적 모델을 활용하고, 심층 생성 모델과 확장 가능한 변이 추론의 최근 발전을 기반으로 유도 및 전환 반지도 학습을 위한 확률 모델을 개발하여 이 질문에 답합니다 (Kingma and Welling, 2014; Rezende et al., 2014).

 

기존 접근 방식 중에서 반지도 학습을 위한 가장 간단한 알고리즘은 자체 학습 방식 (Rosenberg et al., 2005)을 기반으로 합니다. 여기에서 모델은 자신의 매우 확신이 있는 예측에서 얻은 추가 레이블 데이터로 부트스트랩 됩니다. 이 프로세스는 일부 종료 조건에 도달할 때까지 반복됩니다. 이러한 방법은 추론적이며 잘못된 예측을 강화할 수 있기 때문에 오류가 발생하기 쉽습니다. Transductive SVM (TSVM) (Joachims, 1999)은 최대 마진 분류를 목표로 SVM을 확장하는 동시에 마진 근처에 레이블이 지정되지 않은 관측치가 최대한 적도록 합니다. 이러한 접근 방식은 많은 양의 레이블이 지정되지 않은 데이터로 확장하는 데 어려움이 있으며 이 설정에서 효율적인 최적화는 여전히 열려있는 문제입니다. 그래프 기반 방법은 가장 널리 사용되며 유사한 관찰을 연결하는 그래프를 구성하는 것을 목표로 합니다. 레이블 정보는 최소 에너지 (MAP) 구성을 찾아 레이블이 지정된 노드에서 레이블이 없는 노드로 그래프를 통해 전파됩니다 (Blum et al., 2004; Zhu et al., 2003). 그래프 기반 접근 방식은 그래프 구조에 민감하며 효율적인 스펙트럼 방법을 사용할 수 있지만 이러한 방법을 적용할 수 있는 척도를 제한하는 그래프 Laplacian의 고유 분석이 필요합니다 (Fergus et al., 2009). 신경망 기반 접근 방식은 피드 포워드 분류기를 훈련하여 비지도 학습과 지도 학습을 자동 인코더 또는 기타 비지도 데이터 임베딩의 추가 페널티와 결합합니다 (Ranzato and Szummer, 2008; Weston et al., 2012). Manifold Tangent Classifier (MTC) (Rifai et al., 2011)는 대조적 자동 인코더 (CAE)를 훈련하여 데이터가 있는 다양체를 학습한 다음 TangentProp의 인스턴스가 로컬 섭동에 거의 불변하는 분류기를 훈련시킵니다. 다양체를 따라. 그래프 기반 방법을 사용한 다양한 학습 아이디어는 가장 최근에 Atlas RBF 모델 (Pitelis et al., 2014)의 커널 (SVM) 방법과 결합되었으며 현재 사용 가능한 가장 경쟁력 있는 성능을 제공합니다.

 

대신 이 논문에서 우리는 준지도 학습 문제를 분류 문제에 대한 전문화된 결측 데이터 대치 작업으로 인식하는 생성 모델의 힘을 활용하기로 선택합니다. 가우시안 혼합 또는 은닉 마르코프 모델 (Zhu, 2006)과 같은 모델을 기반으로 하는 기존 생성 접근 방식은 많은 수의 혼합물 성분 또는 상태가 잘 수행되어야 하므로 그다지 성공적이지 못했습니다. 더 최근의 솔루션은 트리 (Kemp et al., 2003) 또는 가우스 프로세스 (Adams and Ghahramani, 2009)를 기반으로 하는 비모수 밀도 모델을 사용했지만 이러한 접근 방식에 대한 확장성과 정확한 추론은 여전히 부족합니다. 반 감독 클러스터링에 대한 변이 근사도 이전에 탐구되었습니다 (Li et al., 2009; Wang et al., 2009).

 

따라서 이전에 소규모 생성 접근 방식이 탐색되었지만 준지도 학습을 위한 일반화되고 확장 가능한 확률적 접근 방식은 여전히 부족합니다. 우리가 다음과 같은 기여를 통해 해결하는 것은 이 차이입니다.

• 확률적 모델링과 심층 신경망의 융합으로 형성된 풍부한 매개변수 밀도 추정기를 사용하여 생성 모델을 사용하는 반지도 학습을 위한 새로운 프레임 워크를 설명합니다.
• 반지도 분류 문제에 대해 변분 추론이 어떻게 적용될 수 있는지를 처음으로 제시합니다. 특히, 모델과 변형 매개변수의 공동 최적화를 허용하고 대규모 데이터 세트로 확장 가능한 확률적 변분 추론 알고리즘을 개발합니다.
• 벤치마크 문제에 대한 최신 결과를 제공하는 여러 데이터 세트에 대한 접근 방식의 성능을 보여줍니다.
• 준지도 생성 모델은 데이터 클래스 (콘텐츠 유형)를 클래스 내 변동성 (스타일)에서 분리하는 방법을 학습하여 매우 간단한 방식으로 다양한 데이터 세트에서 이미지의 유사성을 시뮬레이션 할 수 있음을 질적으로 보여줍니다.

---

2. Deep Generative Models for Semi-supervised Learning

We are faced with data that appear as pairs (X, Y) = {(x1, y1), . . . ,(xN , yN )}, with the i-th observation xi ∈ R^D and the corresponding class label yi ∈ {1, . . . , L}. Observations will have corresponding latent variables, which we denote by zi . We will omit the index i whenever it is clear that we are referring to terms associated with a single data point. In semi-supervised classification, only a subset of the observations have corresponding class labels; we refer to the empirical distribution over the labelled and unlabelled subsets as

respectively.

 

We now develop models for semi-supervised learning that exploit generative descriptions of the data to improve upon the classification performance that would be obtained using the labelled data alone.

 

우리는 쌍 (X,Y)={(x1​,y1​),...,(xN​,yN​)}, i 번째 관측치 xi​∈RD 및 해당 클래스 레이블 yi​∈{1,...,L}. 관측치에는 zi​로 표시되는 해당하는 잠재 변수가 있습니다. 단일 데이터 포인트와 관련된 용어를 참조하는 것이 분명할 때마다 인덱스 i를 생략합니다. 준지도 분류에서는 관측치의 하위 집합에만 해당 클래스 레이블이 있습니다. 레이블이 지정된 하위 집합과 레이블이 없는 하위 집합에 대한 경험적 분포를 각각 p~​l​(x,y) 및 p~​u​(x)라고 합니다. 이제 레이블이 지정된 데이터 만 사용하여 얻을 수 있는 분류 성능을 향상시키기 위해 데이터의 생성적 설명을 활용하는 준지도 학습용 모델을 개발합니다.

---

Latent-feature discriminative model (M1):

A commonly used approach is to construct a model that provides an embedding or feature representation of the data. Using these features, a separate classifier is thereafter trained. The embeddings allow for a clustering of related observations in a latent feature space that allows for accurate classification, even with a limited number of labels. Instead of a linear embedding, or features obtained from a regular auto-encoder, we construct a deep generative model of the data that is able to provide a more robust set of latent features. The generative model we use is:

 

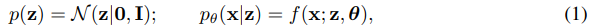
where f(x; z, θ) is a suitable likelihood function (e.g., a Gaussian or Bernoulli distribution) whose probabilities are formed by a non-linear transformation, with parameters θ, of a set of latent variables z. This non-linear transformation is essential to allow for higher moments of the data to be captured by the density model, and we choose these non-linear functions to be deep neural networks.

 

Approximate samples from the posterior distribution over the latent variables p(z|x) are used as features to train a classifier that predicts class labels y, such as a (transductive) SVM or multinomial regression. Using this approach, we can now perform classification in a lower dimensional space since we typically use latent variables whose dimensionality is much less than that of the observations. These low dimensional embeddings should now also be more easily separable since we make use of independent latent Gaussian posteriors whose parameters are formed by a sequence of non-linear transformations of the data. This simple approach results in improved performance for SVMs, and we demonstrate this in section 4.

 

일반적으로 사용되는 접근 방식은 데이터의 임베딩 또는 기능 표현을 제공하는 모델을 구성하는 것입니다. 이러한 기능을 사용하여 별도의 분류기가 훈련됩니다. 임베딩을 사용하면 제한된 수의 레이블로도 정확한 분류를 허용하는 잠재 특징 공간에서 관련 관측 값을 클러스터링 할 수 있습니다. 선형 임베딩 또는 일반 자동 인코더에서 얻은 기능 대신 더 강력한 잠재 기능 세트를 제공할 수 있는 데이터의 심층 생성 모델을 구성합니다. 우리가 사용하는 생성 모델은 다음과 같습니다.

 

여기서 f(x;z,θ)는 잠재 변수 z 세트의 매개 변수 θ를 사용하는 비선형 변환에 의해 확률이 형성되는 적절한 우도 함수 (예 : 가우스 또는 베르누이 분포)입니다. 이 비선형 변환은 밀도 모델에서 데이터의 더 높은 순간을 캡처할 수 있도록 하는데 필수적이며 이러한 비선형 함수를 심층 신경망으로 선택합니다.

 

잠재 변수 p(z∣x)에 대한 사후 분포의 근사 샘플은 (전이적) SVM 또는 다항 회귀와 같은 클래스 레이블 y를 예측하는 분류기를 훈련하는 기능으로 사용됩니다. 이 접근 방식을 사용하면 일반적으로 차원이 관측치보다 훨씬 낮은 잠재 변수를 사용하므로 더 낮은 차원 공간에서 분류를 수행할 수 있습니다. 이러한 저 차원 임베딩은 데이터의 비선형 변환 시퀀스에 의해 매개 변수가 형성되는 독립적인 잠복 가우스 사후를 사용하므로 이제 더 쉽게 분리할 수 있습니다. 이 간단한 접근 방식은 SVM의 성능을 향상시키며 섹션 4에서 이를 보여줍니다.

---

Generative semi-supervised model (M2):

We propose a probabilistic model that describes the data as being generated by a latent class variable y in addition to a continuous latent variable z. The data is explained by the generative process:

 

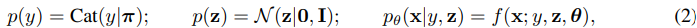
where Cat(y|π) is the multinomial distribution, the class labels y are treated as latent variables if no class label is available and z are additional latent variables. These latent variables are marginally independent and allow us, in case of digit generation for example, to separate the class specification from the writing style of the digit. As before, f(x; y, z, θ) is a suitable likelihood function, e.g., a Bernoulli or Gaussian distribution, parameterised by a non-linear transformation of the latent variables. In our experiments, we choose deep neural networks as this non-linear function. Since most labels y are unobserved, we integrate over the class of any unlabelled data during the inference process, thus performing classification as inference. Predictions for any missing labels are obtained from the inferred posterior distribution pθ(y|x). This model can also be seen as a hybrid continuous-discrete mixture model where the different mixture components share parameters.

 

우리는 연속 잠재 변수 z와 함께 잠재 클래스 변수 y에 의해 생성되는 데이터를 설명하는 확률 모델을 제안합니다. 데이터는 생성 프로세스로 설명됩니다.

 

여기서 Cat(y∣π)는 다항 분포이고, 클래스 레이블을 사용할 수 없고 z가 추가 잠재 변수인 경우 클래스 레이블 y는 잠재 변수로 처리됩니다. 이러한 잠재 변수는 약간 독립적이며, 예를 들어 숫자 생성의 경우 클래스 사양을 숫자의 쓰기 스타일에서 분리할 수 있습니다. 이전과 마찬가지로 f(x;y,z,θ)는 잠재 변수의 비선형 변환으로 매개 변수화된 Bernoulli 또는 Gaussian 분포와 같은 적절한 우도 함수입니다. 실험에서 우리는 이 비선형 함수로 심층 신경망을 선택했습니다. 대부분의 레이블 y는 관찰되지 않기 때문에 추론 프로세스 중에 레이블이 지정되지 않은 모든 데이터의 클래스를 통합하여 추론으로 분류를 수행합니다. 누락된 라벨에 대한 예측은 추론 된 사후 분포 pθ​(y∣x)에서 얻습니다. 이 모델은 서로 다른 혼합물 성분이 매개 변수를 공유하는 하이브리드 연속 이산 혼합물 모델로도 볼 수 있습니다.

---

Stacked generative semi-supervised model (M1+M2):

We can combine these two approaches by first learning a new latent representation z1 using the generative model from M1, and subsequently learning a generative semi-supervised model M2, using embeddings from z1 instead of the raw data x. The result is a deep generative model with two layers of stochastic variables: pθ(x, y, z1, z2) = p(y)p(z2)pθ(z1|y, z2)pθ(x|z1), where the priors p(y) and p(z2) equal those of y and z above, and both pθ(z1|y, z2) and pθ(x|z1) are parameterised as deep neural networks.

 

먼저 M1의 생성 모델을 사용하여 새로운 잠재 표현 z1​을 학습한 다음 원시 데이터 x 대신 z1​의 임베딩을 사용하여 생성적인 반지도 모델 M2를 학습하여 이 두 가지 접근 방식을 결합할 수 있습니다. 결과는 확률적 변수의 두 계층이 있는 심층 생성 모델입니다 :

 

pθ​(x,y,z1​,z2​)=p(y)p(z2​)pθ​(z1​∣y,z2​)pθ​(x∣z1​), 여기서 사전 p(y)와 p(z2​)는 위의 y와 z의 것과 같고 pθ​(z1​∣y,z2​)와 pθ​(x∣z1​)는 모두 심층 신경망으로 매개 변수화됩니다.

---

3. Scalable Variational Inference

3.1 Lower Bound Objective

In all our models, computation of the exact posterior distribution is intractable due to the nonlinear, non-conjugate dependencies between the random variables. To allow for tractable and scalable inference and parameter learning, we exploit recent advances in variational inference (Kingma and Welling, 2014; Rezende et al., 2014). For all the models described, we introduce a fixed-form distribution qφ(z|x) with parameters φ that approximates the true posterior distribution p(z|x). We then follow the variational principle to derive a lower bound on the marginal likelihood of the model – this bound forms our objective function and ensures that our approximate posterior is as close as possible to the true posterior.

 

We construct the approximate posterior distribution qφ(·) as an inference or recognition model, which has become a popular approach for efficient variational inference (Dayan, 2000; Kingma and Welling, 2014; Rezende et al., 2014; Stuhlmuller et al., 2013). Using an inference network, we avoid the need to compute per data point variational parameters, but can instead compute a set of global variational parameters φ. This allows us to amortise the cost of inference by generalising between the posterior estimates for all latent variables through the parameters of the inference network, and allows for fast inference at both training and testing time (unlike with VEM, in which we repeat the generalized E-step optimisation for every test data point). An inference network is introduced for all latent variables, and we parameterise them as deep neural networks whose outputs form the parameters of the distribution qφ(·). For the latent-feature discriminative model (M1), we use a Gaussian inference network qφ(z|x) for the latent variable z. For the generative semi-supervised model (M2), we introduce an inference model for each of the latent variables z and y, which we we assume has a factorised form qφ(z, y|x) = qφ(z|x)qφ(y|x), specified as Gaussian and multinomial distributions respectively.

 

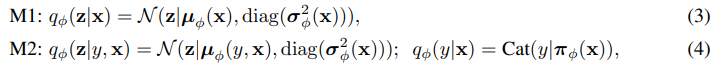
Where σφ(x) is a vector of standard deviations, πφ(x) is a probability vector, and the functions µφ (x), σφ(x) and πφ(x) are represented as MLPs.

3.1.1 Latent Feature Discriminative Model Objective

For this model, the variational bound J(x) on the marginal likelihood for a single data point is:

 

The inference network qφ(z|x) (3) is used during training of the model using both the labelled and unlabelled data sets. This approximate posterior is then used as a feature extractor for the labelled data set, and the features used for training the classifier.

3.1.2 Generative Semi-supervised Model Objective

For this model, we have two cases to consider. In the first case, the label corresponding to a data point is observed and the variational bound is a simple extension of equation (5):

 

for the case where the label is missing, it is treated as a latent variable over which we perform posterior inference and the resulting bound for handling data points with an unobserved label y is:

 

The bound on the marginal likelihood for the entire dataset is now:

 

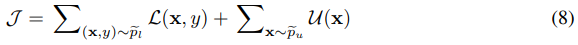
The distribution qφ(y|x) (4) for the missing labels has the form a discriminative classifier, and we can use this knowledge to construct the best classifier possible as our inference model. This distribution is also used at test time for predictions of any unseen data.

 

In the objective function (8), the label predictive distribution qφ(y|x) contributes only to the second term relating to the unlabelled data, which is an undesirable property if we wish to use this distribution as a classifier. Ideally, all model and variational parameters should learn in all cases. To remedy this, we add a classification loss to (8), such that the distribution qφ(y|x) also learns from labelled data. The extended objective function is:

 

where the hyper-parameter α controls the relative weight between generative and purely discriminative learning. We use α = 0.1·N in all experiments. While we have obtained this objective function by motivating the need for all model components to learn at all times, the objective 9 can also be derived directly using the variational principle by instead performing inference over the parameters π of the categorical distribution, using a symmetric Dirichlet prior over these parameters.

---

3.2 Optimisation

The bounds in equations (5) and (9) provide a unified objective function for optimisation of both the parameters θ and φ of the generative and inference models, respectively. This optimisation can be done jointly, without resort to the variational EM algorithm, by using deterministic reparameterisations of the expectations in the objective function, combined with Monte Carlo approximation – referred to in previous work as stochastic gradient variational Bayes (SGVB) (Kingma and Welling, 2014) or as stochastic backpropagation (Rezende et al., 2014). We describe the core strategy for the latent-feature discriminative model M1, since the same computations are used for the generative semi-supervised model.

 

When the prior p(z) is a spherical Gaussian distribution p(z) = N (z|0, I) and the variational distribution qφ(z|x) is also a Gaussian distribution as in (3), the KL term in equation (5) can be computed analytically and the log-likelihood term can be rewritten, using the location-scale transformation for the Gaussian distribution, as:

 

where ⊙ indicates the element-wise product. While the expectation (10) still cannot be solved analytically, its gradients with respect to the generative parameters θ and variational parameters φ can be efficiently computed as expectations of simple gradients:

 

The gradients of the loss (9) for model M2 can be computed by a direct application of the chain rule and by noting that the conditional bound L(xn, y) contains the same type of terms as the loss (9). The gradients of the latter can then be efficiently estimated using (11).

 

During optimization we use the estimated gradients in conjunction with standard stochastic gradientbased optimization methods such as SGD, RMSprop or AdaGrad (Duchi et al., 2010). This results in parameter updates of the form: (θ t+1 , φ t+1) ← (θ t , φ t ) + Γ t (g t θ , g t φ ), where Γ is a diagonal preconditioning matrix that adaptively scales the gradients for faster minimization. The training procedure for models M1 and M2 are summarised in algorithms 1 and 2, respectively. Our experimental results were obtained using AdaGrad.

---

4. Experimental Results

Open source code, with which the most important results and figures can be reproduced, is available at http://github.com/dpkingma/nips14-ssl. For the latest experimental results, please see http://arxiv.org/abs/1406.5298.

4.1 Benchmark Classification

We test performance on the standard MNIST digit classification benchmark. The data set for semisupervised learning is created by splitting the 50,000 training points between a labelled and unlabelled set, and varying the size of the labelled from 100 to 3000. We ensure that all classes are balanced when doing this, i.e. each class has the same number of labelled points. We create a number of data sets using randomised sampling to confidence bounds for the mean performance under repeated draws of data sets.

 

For model M1 we used a 50-dimensional latent variable z. The MLPs that form part of the generative and inference models were constructed with two hidden layers, each with 600 hidden units, using softplus log(1+e^x ) activation functions. On top, a transductive SVM (TSVM) was learned on values of z inferred with qφ(z|x). For model M2 we also used 50-dimensional z. In each experiment, the MLPs were constructed with one hidden layer, each with 500 hidden units and softplus activation functions. In case of SVHN and NORB, we found it helpful to pre-process the data with PCA. This makes the model one level deeper, and still optimizes a lower bound on the likelihood of the unprocessed data.

 

Table 1 shows classification results. We compare to a broad range of existing solutions in semisupervised learning, in particular to classification using nearest neighbours (NN), support vector machines on the labelled set (SVM), the transductive SVM (TSVM), and contractive auto-encoders (CAE). Some of the best results currently are obtained by the manifold tangent classifier (MTC) (Rifai et al., 2011) and the AtlasRBF method (Pitelis et al., 2014). Unlike the other models in this comparison, our models are fully probabilistic but have a cost in the same order as these alternatives.

 

Results: The latent-feature discriminative model (M1) performs better than other models based on simple embeddings of the data, demonstrating the effectiveness of the latent space in providing robust features that allow for easier classification. By combining these features with a classification mechanism directly in the same model, as in the conditional generative model (M2), we are able to get similar results without a separate TSVM classifier.

 

However, by far the best results were obtained using the stack of models M1 and M2. This combined model provides accurate test-set predictions across all conditions, and easily outperforms the previously best methods. We also tested this deep generative model for supervised learning with all available labels, and obtain a test-set performance of 0.96%, which is among the best published results for this permutation-invariant MNIST classification task.

 

표준 MNIST 숫자 분류 벤치마크에서 성능을 테스트합니다. 준지도 학습을 위한 데이터 세트는 레이블이 지정된 세트와 레이블이 없는 세트 사이에 50,000 개의 트레이닝 포인트를 분할하고 레이블이 지정된 크기를 100에서 3000으로 변경하여 생성됩니다. 이를 수행할 때 모든 클래스가 균형을 이루도록 합니다. 즉, 각 클래스가 동일합니다. 레이블이 지정된 포인트의 수입니다. 반복되는 데이터 세트 그리기에서 평균 성능에 대한 신뢰 한계에 대한 무작위 샘플링을 사용하여 많은 데이터 세트를 생성합니다.

 

모델 M1의 경우 50 차원 잠재 변수 z를 사용했습니다. 생성 및 추론 모델의 일부를 구성하는 MLP는 softplus log(1+ex) 활성화 함수를 사용하여 각각 600 개의 은닉 유닛이 있는 두 개의 은닉 계층으로 구성되었습니다. 맨 위에 qφ​(z∣x)로 추론된 z 값에 대해 TSVM (Transductive SVM)을 학습했습니다. 모델 M2의 경우 50 차원 z도 사용했습니다. 각 실험에서 MLP는 각각 500 개의 은닉 유닛과 softplus 활성화 함수가 있는 하나의 은닉 계층으로 구성되었습니다. SVHN 및 NORB의 경우 PCA로 데이터를 사전 처리하는 것이 도움이 된다는 것을 알았습니다. 이는 모델을 한 수준 더 깊게 만들고 처리되지 않은 데이터의 가능성에 대한 하한을 최적화합니다.

 

분류 결과를 표 1에 나타냅니다. 특히 NN (근접 이웃), SVM (Label Set)의 지원 벡터 머신, TSVM (Transductive SVM) 및 CAE (Contractive Auto Encoder)를 사용한 분류와 같은 준지도 학습의 광범위한 기존 솔루션과 비교합니다. 현재 가장 좋은 결과 중 일부는 MTC (manifold tangent classifier) (Rifai et al., 2011)와 AtlasRBF 방법 (Pitelis et al., 2014)을 통해 얻을 수 있습니다. 이 비교에서 다른 모델과 달리, 우리 모델은 완전히 확률적이지만 이러한 대안과 동일한 순서로 비용이 발생합니다.

 

잠재 특징 판별 모델 (M1)은 데이터의 단순한 임베딩을 기반으로 다른 모델보다 더 나은 성능을 발휘하여 쉽게 분류할 수 있는 강력한 기능을 제공하는 데 있어 잠재 공간의 효과를 보여줍니다. 조건부 생성 모델 (M2)에서와 같이 동일한 모델에서 이러한 기능을 분류 메커니즘과 직접 결합하여 별도의 TSVM 분류기 없이 유사한 결과를 얻을 수 있습니다.

 

그러나 모델 M1 및 M2 스택을 사용하여 지금까지 최상의 결과를 얻었습니다. 이 결합된 모델은 모든 조건에서 정확한 테스트 세트 예측을 제공하며 이전에 가장 좋은 방법을 쉽게 능가합니다. 또한 사용 가능한 모든 레이블을 사용하여 지도 학습을 위해 이 심층 생성 모델을 테스트하고 이 순열 불변 MNIST 분류 작업에 대해 가장 잘 게시된 결과 중 하나인 0.96 %의 테스트 세트 성능을 얻었습니다.

---

4.2 Conditional Generation

The conditional generative model can be used to explore the underlying structure of the data, which we demonstrate through two forms of analogical reasoning. Firstly, we demonstrate style and content separation by fixing the class label y, and then varying the latent variables z over a range of values. Figure 1 shows three MNIST classes in which, using a trained model with two latent variables, and the 2D latent variable varied over a range from -5 to 5. In all cases, we see that nearby regions of latent space correspond to similar writing styles, independent of the class; the left region represents upright writing styles, while the right-side represents slanted styles.

 

As a second approach, we use a test image and pass it through the inference network to infer a value of the latent variables corresponding to that image. We then fix the latent variables z to this value, vary the class label y, and simulate images from the generative model corresponding to that combination of z and y. This again demonstrate the disentanglement of style from class. Figure 1 shows these analogical fantasies for the MNIST and SVHN datasets (Netzer et al., 2011). The SVHN data set is a far more complex data set than MNIST, but the model is able to fix the style of house number and vary the digit that appears in that style well. These generations represent the best current performance in simulation from generative models on these data sets.

 

The model used in this way also provides an alternative model to the stochastic feed-forward networks (SFNN) described by Tang and Salakhutdinov (2013). The performance of our model significantly improves on SFNN, since instead of an inefficient Monte Carlo EM algorithm relying on importance sampling, we are able to perform efficient joint inference that is easy to scale.

 

조건부 생성 모델을 사용하여 데이터의 기본 구조를 탐색할 수 있으며, 이는 두 가지 형태의 유추적 추론을 통해 보여줍니다. 먼저, 클래스 레이블 y를 고정한 다음 값 범위에서 잠재 변수 z를 변경하여 스타일과 콘텐츠 분리를 보여줍니다. 그림 1은 두 개의 잠재 변수가 있는 훈련된 모델을 사용하고 2D 잠재 변수가 -5에서 5까지의 범위에서 변하는 세 가지 MNIST 클래스를 보여줍니다. 모든 경우에 잠복의 주변 영역이 비슷한 쓰기 스타일에 해당하는 것을 볼 수 있습니다. 클래스와 무관합니다. 왼쪽 영역은 수직 쓰기 스타일을 나타내고 오른쪽 영역은 기울어진 스타일을 나타냅니다.

 

값, 클래스 레이블 y를 변경하고 z와 y의 해당 조합에 해당하는 생성 모델의 이미지를 시뮬레이션합니다. 이것은 다시 클래스에서 스타일의 분리를 보여줍니다. 그림 1은 MNIST 및 SVHN 데이터 세트에 대한 이러한 비유적 환상을 보여줍니다 (Netzer et al., 2011). SVHN 데이터 세트는 MNIST보다 훨씬 복잡한 데이터 세트이지만 모델은 집 번호의 스타일을 수정할 수 있고 해당 스타일에 잘 나타나는 숫자를 변경할 수 있습니다. 이러한 세대는 이러한 데이터 세트에 대한 생성 모델의 시뮬레이션에서 현재 최고의 성능을 나타냅니다.

 

이러한 방식으로 사용된 모델은 Tang and Salakhutdinov (2013)가 설명한 확률적 피드 포워드 네트워크 (SFNN)에 대한 대안 모델도 제공합니다. 중요도 샘플링에 의존하는 비효율적인 Monte Carlo EM 알고리즘 대신 확장하기 쉬운 효율적인 공동 추론을 수행할 수 있기 때문에 모델의 성능이 SFNN에서 크게 향상되었습니다.

---

4.3 Image Classification

We demonstrate the performance of image classification on the SVHN, and NORB image data sets. Since no comparative results in the semi-supervised setting exists, we perform nearest-neighbour and TSVM classification with RBF kernels and compare performance on features generated by our latent-feature discriminative model to the original features. The results are presented in tables 2 and 3, and we again demonstrate the effectiveness of our approach for semi-supervised classification.

 

SVHN 및 NORB 이미지 데이터 세트에 대한 이미지 분류 성능을 보여줍니다. 반 감독 설정에서 비교 결과가 존재하지 않기 때문에 RBF 커널을 사용하여 가장 가까운 이웃 및 TSVM 분류를 수행하고 잠재 특징 식별 모델에서 생성된 기능의 성능을 원래 기능과 비교합니다. 결과는 표 2와 3에 나와 있으며, 반 감독 분류에 대한 접근 방식의 효율성을 다시 보여줍니다.

---

4.4 Optimization details

The parameters were initialized by sampling randomly from N (0, 0.001^2*I), except for the bias parameters which were initialized as 0. The objectives were optimized using minibatch gradient ascent until convergence, using a variant of RMSProp with momentum and initialization bias correction, a constant learning rate of 0.0003, first moment decay (momentum) of 0.1, and second moment decay of 0.001. For MNIST experiments, minibatches for training were generated by treating normalised pixel intensities of the images as Bernoulli probabilities and sampling binary images from this distribution. In the M2 model, a weight decay was used corresponding to a prior of (θ, φ) ∼ N (0, I).

 

매개 변수는 0으로 초기화된 바이어스 매개 변수를 제외하고 N(0,0.001^2*I)에서 무작위로 샘플링하여 초기화되었습니다. 목표는 모멘텀 및 초기화 바이어스 보정이 있는 RMSProp의 변형을 사용하여 수렴될 때까지 미니 배치 기울기 상승을 사용하여 최적화되었습니다. 0.0003의 일정한 학습률, 0.1의 첫 번째 모멘트 감쇠 (모멘텀) 및 0.001의 두 번째 모멘트 감쇠. MNIST 실험의 경우 이미지의 정규화 된 픽셀 강도를 Bernoulli 확률로 처리하고 이 분포에서 이진 이미지를 샘플링하여 훈련을 위한 미니 배치를 생성했습니다. M2 모델에서는 (θ,φ)∼N(0,I)의 사전에 해당하는 가중치 감쇠를 사용했습니다.

---

5. Discussion and Conclusion

The approximate inference methods introduced here can be easily extended to the model’s parameters, harnessing the full power of variational learning. Such an extension also provides a principled ground for performing model selection. Efficient model selection is particularly important when the amount of available data is not large, such as in semi-supervised learning.

 

For image classification tasks, one area of interest is to combine such methods with convolutional neural networks that form the gold-standard for current supervised classification methods. Since all the components of our model are parametrised by neural networks we can readily exploit convolutional or more general locally-connected architectures – and forms a promising avenue for future exploration.

 

A limitation of the models we have presented is that they scale linearly in the number of classes in the data sets. Having to re-evaluate the generative likelihood for each class during training is an expensive operation. Potential reduction of the number of evaluations could be achieved by using a truncation of the posterior mass. For instance we could combine our method with the truncation algorithm suggested by Pal et al. (2005), or by using mechanisms such as error-correcting output codes (Dietterich and Bakiri, 1995). The extension of our model to multi-label classification problems that is essential for image-tagging is also possible, but requires similar approximations to reduce the number of likelihood-evaluations per class.

 

We have developed new models for semi-supervised learning that allow us to improve the quality of prediction by exploiting information in the data density using generative models. We have developed an efficient variational optimisation algorithm for approximate Bayesian inference in these models and demonstrated that they are amongst the most competitive models currently available for semisupervised learning. We hope that these results stimulate the development of even more powerful semi-supervised classification methods based on generative models, of which there remains much scope.

 

여기에 소개된 근사 추론 방법은 변형 학습의 모든 기능을 활용하여 모델의 매개 변수로 쉽게 확장할 수 있습니다. 이러한 확장은 또한 모델 선택을 수행하기 위한 원칙적인 근거를 제공합니다. 반지도 학습과 같이 사용 가능한 데이터의 양이 많지 않을 때 효율적인 모델 선택이 특히 중요합니다.

 

이미지 분류 작업의 경우 관심 분야 중 하나는 이러한 방법을 현재 감독되는 분류 방법의 표준을 형성하는 컨볼루션 신경망과 결합하는 것입니다. 모델의 모든 구성 요소가 신경망에 의해 매개 변수화되기 때문에 컨볼루션 또는 보다 일반적인 로컬 연결 아키텍처를 쉽게 활용할 수 있으며 향후 탐색을 위한 유망한 길을 형성합니다.

 

우리가 제시한 모델의 한계는 데이터 세트의 클래스 수에서 선형적으로 확장된다는 것입니다. 훈련 중에 각 클래스의 생성 가능성을 재평가해야 하는 것은 비용이 많이 드는 작업입니다. 후방 질량의 절단을 사용하여 평가 횟수를 잠재적으로 줄일 수 있습니다. 예를 들어 우리는 우리의 방법을 Pal et al. 이 제안한 절단 알고리즘과 결합할 수 있습니다. (2005) 또는 오류 수정 출력 코드와 같은 메커니즘을 사용합니다 (Dietterich 및 Bakiri, 1995). 이미지 태깅에 필수적인 다중 라벨 분류 문제로 모델을 확장하는 것도 가능하지만 클래스 당 가능성 평가 수를 줄이기 위해 유사한 근사치가 필요합니다.

 

우리는 생성 모델을 사용하여 데이터 밀도의 정보를 활용하여 예측의 품질을 향상시킬 수 있는 반지도 학습을 위한 새로운 모델을 개발했습니다. 우리는 이러한 모델에서 근사 베이지안 추론을 위한 효율적인 변형 최적화 알고리즘을 개발했으며 현재 준지도 학습에 사용할 수 있는 가장 경쟁력 있는 모델 중 하나임을 입증했습니다. 우리는 이러한 결과가 생성 모델을 기반으로 한 훨씬 더 강력한 반 감독 분류 방법의 개발을 촉진하기를 희망합니다.