[AAE] Adversasrial Autoencoders

https://arxiv.org/pdf/1511.05644

---

Abstract

In this paper, we propose the “adversarial autoencoder” (AAE), which is a probabilistic autoencoder that uses the recently proposed generative adversarial networks (GAN) to perform variational inference by matching the aggregated posterior of the hidden code vector of the autoencoder with an arbitrary prior distribution. Matching the aggregated posterior to the prior ensures that generating from any part of prior space results in meaningful samples. As a result, the decoder of the adversarial autoencoder learns a deep generative model that maps the imposed prior to the data distribution. We show how the adversarial autoencoder can be used in applications such as semi-supervised classification, disentangling style and content of images, unsupervised clustering, dimensionality reduction and data visualization. We performed experiments on MNIST, Street View House Numbers and Toronto Face datasets and show that adversarial autoencoders achieve competitive results in generative modeling and semi-supervised classification tasks.

---

1. Introduction

Building scalable generative models to capture rich distributions such as audio, images or video is one of the central challenges of machine learning. Until recently, deep generative models, such as Restricted Boltzmann Machines (RBM), Deep Belief Networks (DBNs) and Deep Boltzmann Machines (DBMs) were trained primarily by MCMC-based algorithms [Hinton et al., 2006, Salakhutdinov and Hinton, 2009]. In these approaches the MCMC methods compute the gradient of log-likelihood which becomes more imprecise as training progresses. This is because samples from the Markov Chains are unable to mix between modes fast enough. In recent years, generative models have been developed that may be trained via direct back-propagation and avoid the difficulties that come with MCMC training. For example, variational autoencoders (VAE) [Kingma and Welling, 2014, Rezende et al., 2014] or importance weighted autoencoders [Burda et al., 2015] use a recognition network to predict the posterior distribution over the latent variables, generative adversarial networks (GAN) [Goodfellow et al., 2014] use an adversarial training procedure to directly shape the output distribution of the network via back-propagation and generative moment matching networks (GMMN) [Li et al., 2015] use a moment matching cost function to learn the data distribution.

 

In this paper, we propose a general approach, called an adversarial autoencoder (AAE) that can turn an autoencoder into a generative model. In our model, an autoencoder is trained with dual objectives – a traditional reconstruction error criterion, and an adversarial training criterion [Goodfellow et al., 2014] that matches the aggregated posterior distribution of the latent representation of the autoencoder to an arbitrary prior distribution. We show that this training criterion has a strong connection to VAE training. The result of the training is that the encoder learns to convert the data distribution to the prior distribution, while the decoder learns a deep generative model that maps the imposed prior to the data distribution.

---

1.1. Generative Adversarial Networks

The Generative Adversarial Networks (GAN) [Goodfellow et al., 2014] framework establishes a min-max adversarial game between two neural networks – a generative model, G, and a discriminative model, D. The discriminator model, D(x), is a neural network that computes the probability that a point x in data space is a sample from the data distribution (positive samples) that we are trying to model, rather than a sample from our generative model (negative samples). Concurrently, the generator uses a function G(z) that maps samples z from the prior p(z) to the data space. G(z) is trained to maximally confuse the discriminator into believing that samples it generates come from the data distribution. The generator is trained by leveraging the gradient of D(x) w.r.t. x, and using that to modify its parameters. The solution to this game can be expressed as following [Goodfellow et al., 2014]:

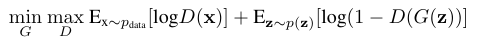
The generator G and the discriminator D can be found using alternating SGD in two stages: (a) Train the discriminator to distinguish the true samples from the fake samples generated by the generator. (b) Train the generator so as to fool the discriminator with its generated samples.

---

2. Adversarial Autoencoders

Let x be the input and z be the latent code vector (hidden units) of an autoencoder with a deep encoder and decoder. Let p(z) be the prior distribution we want to impose on the codes, q(z|x) be an encoding distribution and p(x|z) be the decoding distribution. Also let pd(x) be the data distribution, and p(x) be the model distribution. The encoding function of the autoencoder q(z|x) defines an aggregated posterior distribution of q(z) on the hidden code vector of the autoencoder as follows:

The adversarial autoencoder is an autoencoder that is regularized by matching the aggregated posterior, q(z), to an arbitrary prior, p(z). In order to do so, an adversarial network is attached on top of the hidden code vector of the autoencoder as illustrated in Figure 1. It is the adversarial network that guides q(z) to match p(z). The autoencoder, meanwhile, attempts to minimize the reconstruction error. The generator of the adversarial network is also the encoder of the autoencoder q(z|x). The encoder ensures the aggregated posterior distribution can fool the discriminative adversarial network into thinking that the hidden code q(z) comes from the true prior distribution p(z).

 

Both, the adversarial network and the autoencoder are trained jointly with SGD in two phases – the reconstruction phase and the regularization phase – executed on each mini-batch. In the reconstruction phase, the autoencoder updates the encoder and the decoder to minimize the reconstruction error of the inputs. In the regularization phase, the adversarial network first updates its discriminative network to tell apart the true samples (generated using the prior) from the generated samples (the hidden codes computed by the autoencoder). The adversarial network then updates its generator (which is also the encoder of the autoencoder) to confuse the discriminative network.

 

Once the training procedure is done, the decoder of the autoencoder will define a generative model that maps the imposed prior of p(z) to the data distribution.

 

---

2.1. Relationship to Variational Autoencoders

 

Our work is similar in spirit to variational autoencoders [Kingma and Welling, 2014]; however, while they use a KL divergence penalty to impose a prior distribution on the hidden code vector of the autoencoder, we use an adversarial training procedure to do so by matching the aggregated posterior of the hidden code vector with the prior distribution.

 

VAE [Kingma and Welling, 2014] minimizes the following upper-bound on the negative log-likelihood of x:

where the aggregated posterior q(z) is defined in Eq. (1) and we have assumed q(z|x) is Gaussian and p(z) is an arbitrary distribution. The variational bound contains three terms. The first term can be viewed as the reconstruction term of an autoencoder and the second and third terms can be viewed as regularization terms. Without the regularization terms, the model is simply a standard autoencoder that reconstructs the input. However, in the presence of the regularization terms, the VAE learns a latent representation that is compatible with p(z). The second term of the cost function encourages large variances for the posterior distribution while the third term minimizes the cross-entropy between the aggregated posterior q(z) and the prior p(z). KL divergence or the cross-entropy term in Eq. (2), encourages q(z) to pick the modes of p(z). In adversarial autoencoders, we replace the second two terms with an adversarial training procedure that encourages q(z) to match to the whole distribution of p(z).

 

In this section, we compare the ability of the adversarial autoencoder to the VAE to impose a specified prior distribution p(z) on the coding distribution. Figure 2a shows the coding space z of the test data resulting from an adversarial autoencoder trained on MNIST digits in which a spherical 2-D Gaussian prior distribution is imposed on the hidden codes z. The learned manifold in Figure 2a exhibits sharp transitions indicating that the coding space is filled and exhibits no “holes”. In practice, sharp transitions in the coding space indicate that images generated by interpolating within z lie on the data manifold (Figure 2e). By contrast, Figure 2c shows the coding space of a VAE with the same architecture used in the adversarial autoencoder experiments. We can see that in this case the VAE roughly matches the shape of a 2-D Gaussian distribution. However, no data points map to several local regions of the coding space indicating that the VAE may not have captured the data manifold as well as the adversarial autoencoder.

 

Figures 2b and 2d show the code space of an adversarial autoencoder and of a VAE where the imposed distribution is a mixture of 10 2-D Gaussians. The adversarial autoencoder successfully matched the aggregated posterior with the prior distribution (Figure 2b). In contrast, the VAE exhibit systematic differences from the mixture 10 Gaussians indicating that the VAE emphasizes matching the modes of the distribution as discussed above (Figure 2d).

 

An important difference between VAEs and adversarial autoencoders is that in VAEs, in order to back-propagate through the KL divergence by Monte-Carlo sampling, we need to have access to the exact functional form of the prior distribution. However, in AAEs, we only need to be able to sample from the prior distribution in order to induce q(z) to match p(z). In Section 2.3, we will demonstrate that the adversarial autoencoder can impose complicated distributions (e.g., swiss roll distribution) without having access to the explicit functional form of the distribution.

---

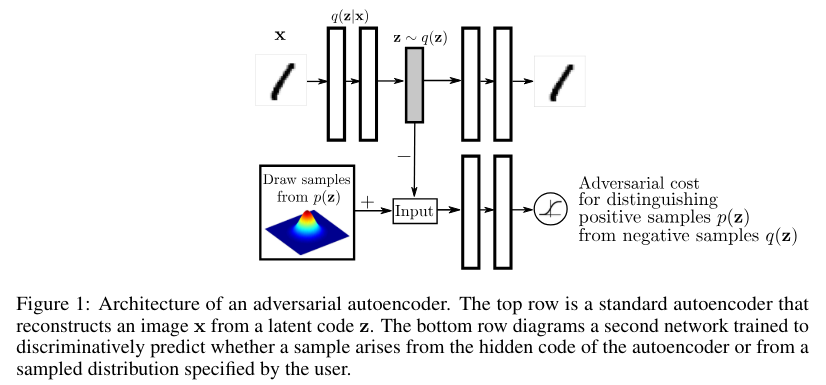
2.3. Incorporating Label Information in the Adversarial Regularization

 

In the scenarios where data is labeled, we can incorporate the label information in the adversarial training stage to better shape the distribution of the hidden code. In this section, we describe how to leverage partial or complete label information to regularize the latent representation of the autoencoder more heavily. To demonstrate this architecture we return to Figure 2b in which the adversarial autoencoder is fit to a mixture of 10 2-D Gaussians. We now aim to force each mode of the mixture of Gaussian distribution to represent a single label of MNIST.

 

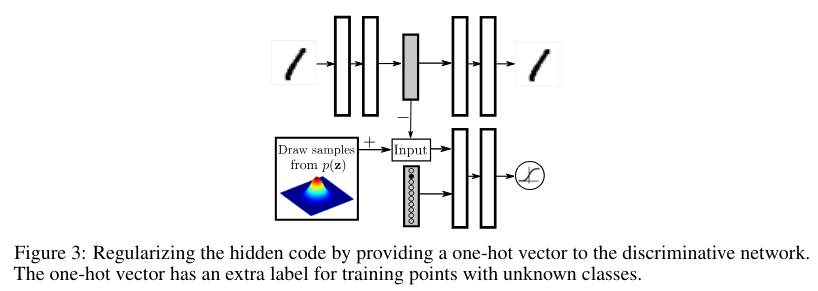
Figure 3 demonstrates the training procedure for this semi-supervised approach. We add a onehot vector to the input of the discriminative network to associate the label with a mode of the distribution. The one-hot vector acts as switch that selects the corresponding decision boundary of the discriminative network given the class label. This one-hot vector has an extra class for unlabeled examples. For example, in the case of imposing a mixture of 10 2-D Gaussians (Figure 2b and 4a), the one hot vector contains 11 classes. Each of the first 10 class selects a decision boundary for the corresponding individual mixture component. The extra class in the one-hot vector corresponds to unlabeled training points. When an unlabeled point is presented to the model, the extra class is turned on, to select the decision boundary for the full mixture of Gaussian distribution. During the positive phase of adversarial training, we provide the label of the mixture component (that the positive sample is drawn from) to the discriminator through the one-hot vector. The positive samples fed for unlabeled examples come from the full mixture of Gaussian, rather than from a particular class. During the negative phase, we provide the label of the training point image to the discriminator through the one-hot vector.

 

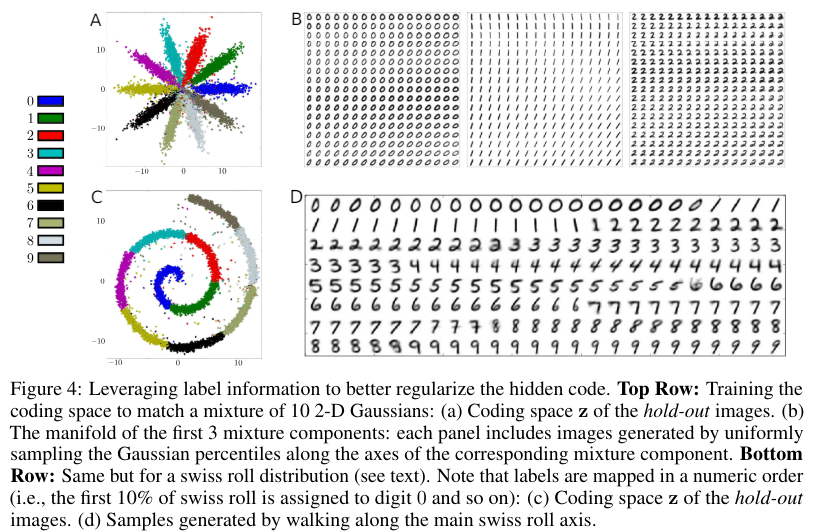
Figure 4a shows the latent representation of an adversarial autoencoder trained with a prior that is a mixture of 10 2-D Gaussians trained on 10K labeled MNIST examples and 40K unlabeled MNIST examples. In this case, the i-th mixture component of the prior has been assigned to the i-th class in a semi-supervised fashion. Figure 4b shows the manifold of the first three mixture components. Note that the style representation is consistently represented within each mixture component, independent of its class. For example, the upper-left region of all panels in Figure 4b correspond to the upright writing style and lower-right region of these panels correspond to the tilted writing style of digits.

 

This method may be extended to arbitrary distributions with no parametric forms – as demonstrated by mapping the MNIST data set onto a “swiss roll” (a conditional Gaussian distribution whose mean is uniformly distributed along the length of a swiss roll axis). Figure 4c depicts the coding space z and Figure 4d highlights the images generated by walking along the swiss roll axis in the latent space.

---

8. Conclusion

In this paper, we proposed to use the GAN framework as a variational inference algorithm for both discrete and continuous latent variables in probabilistic autoencoders. Our method called the adversarial autoencoder (AAE), is a generative autoencoder that achieves competitive test likelihoods on real-valued MNIST and Toronto Face datasets. We discussed how this method can be extended to semi-supervised scenarios and showed that it achieves competitive semi-supervised classification performance on MNIST and SVHN datasets. Finally, we demonstrated the applications of adversarial autoencoders in disentangling the style and content of images, unsupervised clustering, dimensionality reduction and data visualization.