Normalizing Flows Tutorial, Part 2: Modern Normalizing Flows

https://blog.evjang.com/2018/01/nf2.html

---

In my previous blog post, I described how simple distributions like Gaussians can be “deformed” to fit complex data distributions using normalizing flows. We implemented a simple flow by chaining 2D Affine Bijectors with PreLU nonlinearities to build a small invertible neural net.

 

However, this MLP flow is pretty weak: there are only 2 units per hidden layer. Furthermore, the non-linearity is monotonic and piecewise linear, so all it does is slightly warp the data manifold around the origin. This flow completely fails to implement more complex transformations like separating an isotropic Gaussian into two modes when trying to learn the “Two Moons” dataset below:

Fortunately, there are several more powerful normalizing flows that have been introduced in recent Machine Learning literature. We will explore several of these techniques in this tutorial.

---

Autoregressive Models and Normalizing Flows

Autoregressive density estimation techniques like WaveNet and PixelRNN model learn complex joint densities p(x1:D) by decomposing the joint density into a product of one-dimensional conditional densities, where each xi depends on only the previous i−1 values:

The conditional densities usually have learnable parameters. For example, a common choice is an autoregressive density p(x1:D) whose conditional density is a univariate Gaussian, whose mean and standard deviations are computed by neural networks that depend on the previous x1:i−1.

 

Learning data with autoregressive density estimation makes the rather bold inductive bias that the ordering of variables are such that your earlier variables don’t depend on later variables. Intuitively, this shouldn’t be true at all for natural data (the top row of pixels in an image does have a causal, conditional dependency on the bottom of the image). However it’s still possible to generate plausible images in this manner (to the surprise of many researchers!). 

 

To sample from this distribution, we compute D “noise variates” u1:D from the standard Normal, N(0,1), then apply the following recursion to get x1:D.

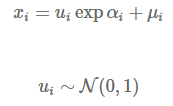
The procedure of autoregressive sampling is a deterministic transformation of the underlying noise variates (sampled from N(0,I)) into a new distribution, so autoregressive samples can actually be interpreted as a TransformedDistribution of the standard Normal!

 

Armed with this insight, we can stack multiple autoregressive transformations into a normalizing flow. The advantage of doing this is that we can change the ordering of variables x1,...xD for each bijector in the flow, so that if one autoregressive factorization cannot model a distribution well (due to a poor choice of variable ordering), a subsequent layer might be able to do it.

 

The Masked Autoregressive Flow (MAF) bijector implements such a conditional-Gaussian autoregressive model. Here is a schematic of the forward pass for a single entry in a sample of the transformed distribution, xi:

 

The gray unit xi is the unit we are trying to compute, and the blue units are the values it depends on. αi and μi are scalars that are computed by passing x1:i−1 through neural networks (magenta, orange circles). Even though the transformation is a mere scale-and-shift, the scale and shift can have complex dependencies on previous variables. For the first unit x1, μ and α are usually set to learnable scalar variables that don’t depend on any x or u.

 

More importantly, the transformation is designed this way so that computing the inverse u=f−1(x) does not require us to invert fα or fμ. Because the transformation is parameterized as a scale-and-shift, we can recover the original noise variates by reversing the shift and scale: u=(x−fμ(x))/exp(fα(x)). The forward and inverse pass of the bijector only depend on the forward evaluation of fα(x) and fμ(x), allowing us to use non-invertible functions like ReLU and non-square matrix multiplication in the neural networks fμ and fα.

 

The inverse pass of the MAF model is used to evaluate density:

---

Runtime Complexity and MADE

Autoregressive models and MAF can be trained “quickly” because all conditional likelihoods p(x1),p(x2|x1),...p(xD|x1:D−1)) can be evaluated simultaneously in a single pass of D threads, leveraging the batch parallelism of modern GPUs. We are operating under the assumption that parallelism, such as SIMD vectorization on CPUs/GPUs, has zero runtime overhead.

 

On the other hand, sampling autoregressive models is slow because you must wait for all previous x1:i−1 to be computed before computing new xi. The runtime complexity of generating a single sample is D sequential passes of a single thread, which fails to exploit processor parallelism.

 

Another issue: in the parallelizable inverse pass, should we use separate neural nets (with differently-sized inputs) for computing each αi and μi? That's inefficient, especially if we consider that learned representations between these D networks should be shared (as long as the autoregressive dependency is not violated). In the Masked Autoencoder for Distribution Estimation (MADE) paper, the authors propose a very nice solution: use a single neural net to output all values of α and μ simultaneously, but mask the weights so that the autoregressive property is preserved.

 

This trick makes it possible to recover all values of u from all values of x with a single pass through a single neural network (D inputs, D outputs). This is far more efficient than processing D neural networks simultaneously (D(D+1)/2 inputs, D outputs).

 

To summarize, MAF uses the MADE architecture as an efficiency trick for computing nonlinear parameters of shift-and-scale autoregressive transformations, and casts these efficient autoregressive models into the normalizing flows framework.

---

Inverse Autoregressive Flow (IAF)

In Inverse Autoregressive Flow, the nonlinear shift/scale statistics are computed using the previous noise variates u1:i−1, instead of the data samples:

 

The forward (sampling) pass of IAF is fast: all the xi can be computed in a single pass of D threads working in parallel. IAF also uses MADE networks to implement this parallelism efficiently.

 

However, if we are given a new data point and asked to evaluate the density, we need to recover u and this process is slow: first we recover u1=(x−μ1)∗exp(−α1), then ui=(x−μi(u1:i−1))∗exp(−αi(u1:i−1)) sequentially. On the other hand, it’s trivial to track the (log) probability of samples generated by IAF, since we already know all of the u values to begin with without having to invert from x.

 

The astute reader will notice that if you re-label the bottom row as x_1, .. x_D, and the top row as u_1, … u_D, this is exactly equivalent to the Inverse Pass of the MAF bijector! Likewise, the inverse of IAF is nothing more than the forward pass of MAF (with x and u swapped). 

 

IAF and MAF make opposite computational tradeoffs - MAF trains quickly but samples slowly, while IAF trains slowly but samples quickly. For training neural networks, we usually demand way more throughput with density evaluation than sampling, so MAF is usually a more appropriate choice when learning distributions.

---

Parallel Wavenet

An obvious follow-up question is whether these two approaches can be combined to get the best of both worlds, i.e. fast training and sampling.

 

The answer is yes! The much-publicized Parallel Wavenet by DeepMind does exactly this: an autoregressive model (MAF) is used to train a generative model efficiently, then an IAF model is trained to maximize the likelihood of its own samples under this teacher. Recall that with IAF, it is costly to compute density of external data points (such as those from the training set), but it can cheaply compute density of its own samples by caching the noise variates u1:D, thereby circumventing the need to call the inverse pass. Thus, we can train the “student” IAF model by minimizing the divergence between the student and teacher distributions.

 

This is an incredibly impactful application of normalizing flows research - the end result is a real-time audio synthesis model that is 20 times faster to sample, and is already deployed in real-world products like the Google Assistant.

---

NICE and Real-NVP

Finally, we consider is Real-NVP, which can be thought of as a special case of the IAF bijector.

 

In a NVP “coupling layer”, we fix an integer 0<d<D. Like IAF, xd+1 is a shift-and-scale that depends on previous ud values. The difference is that we also force xd+2,xd+3,…xD to only depend on these ud values, so a single network pass can be used to produce αd+1:D and μd+1:D.

 

As for x1:d they are “pass-through” units that are set equivalently tou1:d. Therefore, Real-NVP is also a special case of the MAF bijector (since α(u1:d)=α(x1:d)).

 

Because the shift-and-scale statistics for the whole layer can be computed from either x1:d or u1:d in a single pass, NVP can perform forward and inverse computations in a single parallel pass (sampling and estimation are both fast). MADE is also not needed.

 

However, empirical studies suggest that Real-NVP tends to underperform MAF and IAF and my experience has been that NVP tends to fit my toy 2D datasets (e.g. SIGGRAPH dataset) more poorly when using the same number of layers. Real-NVP and IAF are nearly equivalent in the 2D case, except the first unit of IAF is still transformed via a scale-and-shift that does not depend on u1, while Real-NVP leaves the first unit unmodified.

 

Real-NVP was a follow-up work to the NICE bijector, which is a shift-only variant that assumes α=0. Because NICE does not scale the distribution, the ILDJ is actually constant!

---

Discussion

When deciding which Normalizing Flow to use, consider the design tradeoff between a fast forward pass and a fast inverse pass, as well as between an expressive flow and a speedy ILJD.

 

In Part 1 of the tutorial, I motivated Normalizing Flows by saying that we need availability of more powerful distributions that can be used in reinforcement learning and generative modeling. In the big picture of things, it’s not clear whether having volume-tracking normalizing flows is actually the best tool for AI applications like robotics, structured prediction, when techniques like variational inference and implicit density models already work extremely well in practice. Even still, normalizing flows are a neat family of methods to have in your back pocket and they have demonstrable real-world applications, such as in real-time generative audio models deployed on Google Assistant.

 

Although explicit-density models like normalizing flows are amenable to training via maximum likelihood, this is not the only way they can be used and are complementary to VAEs and GANs. It’s possible to use normalizing flow as a drop-in replacement for anywhere you would use a Gaussian, such as VAE priors and latent codes in GANs. For example, this paper use normalizing flows as flexible variational priors, and the TensorFlow distributions paper presents a VAE that uses a normalizing flow as a prior along with a PixelCNN decoder. Parallel Wavenet trains an IAF "student" model via KL divergence.

 

One of the most intriguing properties of normalizing flows is that they implement reversible computation (i.e. have a defined inverse of an expressive function). This means that if we want to perform a backprop pass, we can re-compute the forward activation values without having to store them in memory during the forward pass (potentially expensive for large graphs). In a setting where credit assignment may take place over very long time scales, we can use reversible computation to “recover” past decision states while keeping memory usage bounded. In fact, this idea was utilized in the RevNets paper, and was actually inspired by the invertibility of the NICE bijector. I’m reminded of the main character from the film Memento who is unable to store memories, so he uses invertible compute to remember things.