Variational Inference with Normalizing Flows

https://arxiv.org/pdf/1505.05770

---

Abstract

The choice of approximate posterior distribution is one of the core problems in variational inference. Most applications of variational inference employ simple families of posterior approximations in order to allow for efficient inference, focusing on mean-field or other simple structured approximations. This restriction has a significant impact on the quality of inferences made using variational methods. We introduce a new approach for specifying flexible, arbitrarily complex and scalable approximate posterior distributions. Our approximations are distributions constructed through a normalizing flow, whereby a simple initial density is transformed into a more complex one by applying a sequence of invertible transformations until a desired level of complexity is attained. We use this view of normalizing flows to develop categories of finite and infinitesimal flows and provide a unified view of approaches for constructing rich posterior approximations. We demonstrate that the theoretical advantages of having posteriors that better match the true posterior, combined with the scalability of amortized variational approaches, provides a clear improvement in performance and applicability of variational inference.

---

1. Introduction

There has been a great deal of renewed interest in variational inference as a means of scaling probabilistic modeling to increasingly complex problems on increasingly larger data sets. Variational inference now lies at the core of large-scale topic models of text (Hoffman et al., 2013), provides the state-of-the-art in semi-supervised classification (Kingma et al., 2014), drives the models that currently produce the most realistic generative models of images (Gregor et al., 2014; 2015; Rezende et al., 2014; Kingma & Welling, 2014), and are a default tool for the understanding of many physical and chemical systems. Despite these successes and ongoing advances, there are a number of disadvantages of variational methods that limit their power and hamper their wider adoption as a default method for statistical inference. It is one of these limitations, the choice of posterior approximation, that we address in this paper.

 

Variational inference requires that intractable posterior distributions be approximated by a class of known probability distributions, over which we search for the best approximation to the true posterior. The class of approximations used is often limited, e.g., mean-field approximations, implying that no solution is ever able to resemble the true posterior distribution. This is a widely raised objection to variational methods, in that unlike other inferential methods such as MCMC, even in the asymptotic regime we are unable recover the true posterior distribution.

 

There is much evidence that richer, more faithful posterior approximations do result in better performance. For example, when compared to sigmoid belief networks that make use of mean-field approximations, deep auto-regressive networks use a posterior approximation with an autoregressive dependency structure that provides a clear improvement in performance (Mnih & Gregor, 2014). There is also a large body of evidence that describes the detrimental effect of limited posterior approximations. Turner & Sahani (2011) provide an exposition of two commonly experienced problems. The first is the widely-observed problem of under-estimation of the variance of the posterior distribution, which can result in poor predictions and unreliable decisions based on the chosen posterior approximation. The second is that the limited capacity of the posterior approximation can also result in biases in the MAP estimates of any model parameters (and this is the case e.g., in time-series models).

 

A number of proposals for rich posterior approximations have been explored, typically based on structured meanfield approximations that incorporate some basic form of dependency within the approximate posterior. Another potentially powerful alternative would be to specify the approximate posterior as a mixture model, such as those developed by Jaakkola & Jordan (1998); Jordan et al. (1999); Gershman et al. (2012). But the mixture approach limits the potential scalability of variational inference since it requires evaluation of the log-likelihood and its gradients for each mixture component per parameter update, which is typically computationally expensive.

 

This paper presents a new approach for specifying approximate posterior distributions for variational inference. We begin by reviewing the current best practice for inference in general directed graphical models, based on amortized variational inference and efficient Monte Carlo gradient estimation, in section 2. We then make the following contributions: 

• We propose the specification of approximate posterior distributions using normalizing flows, a tool for constructing complex distributions by transforming a probability density through a series of invertible mappings (sect. 3). Inference with normalizing flows provides a tighter, modified variational lower bound with additional terms that only add terms with linear time complexity (sect 4).
• We show that normalizing flows admit infinitesimal flows that allow us to specify a class of posterior approximations that in the asymptotic regime is able to recover the true posterior distribution, overcoming one oft-quoted limitation of variational inference.
• We present a unified view of related approaches for improved posterior approximation as the application of special types of normalizing flows (sect 5).
• We show experimentally that the use of general normalizing flows systematically outperforms other competing approaches for posterior approximation.

---

2. Amortized Variational Inference

To perform inference it is sufficient to reason using the marginal likelihood of a probabilistic model, and requires the marginalization of any missing or latent variables in the model. This integration is typically intractable, and instead, we optimize a lower bound on the marginal likelihood. Consider a general probabilistic model with observations x, latent variables z over which we must integrate, and model parameters θ. We introduce an approximate posterior distribution for the latent variables qφ(z|x) and follow the variational principle (Jordan et al., 1999) to obtain a bound on the marginal likelihood:

 

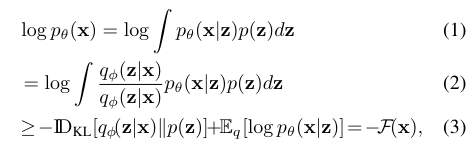
where we used Jensen’s inequality to obtain the final equation, pθ(x|z) is a likelihood function and p(z) is a prior over the latent variables. We can easily extend this formulation to posterior inference over the parameters θ, but we will focus on inference over the latent variables only. This bound is often referred to as the negative free energy F or as the evidence lower bound (ELBO). It consists of two terms: the first is the KL divergence between the approximate posterior and the prior distribution (which acts as a regularizer), and the second is a reconstruction error. This bound (3) provides a unified objective function for optimization of both the parameters θ and φ of the model and variational approximation, respectively.

 

Current best practice in variational inference performs this optimization using mini-batches and stochastic gradient descent, which is what allows variational inference to be scaled to problems with very large data sets. There are two problems that must be addressed to successfully use the variational approach: 1) efficient computation of the derivatives of the expected loglikelihood ∇φEqφ(z) [log pθ(x|z)], and 2) choosing the richest, computationally-feasible approximate posterior distribution q(·). The second problem is the focus of this paper. To address the first problem, we make use of two tools: Monte Carlo gradient estimation and inference networks, which when used together is what we refer to as amortized variational inference.

---

2.1. Stochastic Backpropagation

The bulk of research in variational inference over the years has been on ways in which to compute the gradient of the expected log-likelihood ∇φEqφ(z) [log p(x|z)]. Whereas we would have previously resorted to local variational methods (Bishop, 2006), in general we now always compute such expectations using Monte Carlo approximations (including the KL term in the bound, if it is not analytically known). This forms what has been aptly named doublystochastic estimation (Titsias & Lazaro-Gredilla, 2014), since we have one source of stochasticity from the minibatch and a second from the Monte Carlo approximation of the expectation.

 

We focus on models with continuous latent variables, and the approach we take computes the required gradients using a non-centered reparameterization of the expectation (Papaspiliopoulos et al., 2003; Williams, 1992), combined with Monte Carlo approximation — referred to as stochastic backpropagation (Rezende et al., 2014). This approach has also been referred to or as stochastic gradient variational Bayes (SGVB) (Kingma & Welling, 2014) or as affine variational inference (Challis & Barber, 2012).

 

Stochastic backpropagation involves two steps:

• Reparameterization. We reparameterize the latent variable in terms of a known base distribution and a differentiable transformation (such as a location-scale transformation or cumulative distribution function). For example, if qφ(z) is a Gaussian distribution N (z|µ, σ2 ), with φ = {µ, σ2}, then the location-scale transformation using the standard Normal as a base distribution allows us to reparameterize z as: 

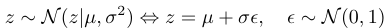
• Backpropagation with Monte Carlo. We can now differentiate (backpropagation) w.r.t. the parameters φ of the variational distribution using a Monte Carlo approximation with draws from the base distribution:

 

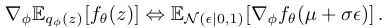
A number of general purpose approaches based on Monte Carlo control variate (MCCV) estimators exist as an alternative to stochastic backpropagation, and allow for gradient computation with latent variables that may be continuous or discrete (Williams, 1992; Mnih & Gregor, 2014; Ranganath et al., 2013; Wingate & Weber, 2013). An important advantage of stochastic backpropagation is that, for models with continuous latent variables, it has the lowest variance among competing estimators.

---

2.2. Inference Networks

A second important practice is that the approximate posterior distribution qφ(·) is represented using a recognition model or inference network (Rezende et al., 2014; Dayan, 2000; Gershman & Goodman, 2014; Kingma & Welling, 2014). An inference network is a model that learns an inverse map from observations to latent variables. Using an inference network, we avoid the need to compute per data point variational parameters, but can instead compute a set of global variational parameters φ valid for inference at both training and test time. This allows us to amortize the cost of inference by generalizing between the posterior estimates for all latent variables through the parameters of the inference network. The simplest inference models that we can use are diagonal Gaussian densities, qφ(z|x) = N (z|µφ(x), diag(σ2φ(x))), where the mean function µφ(x) and the standard-deviation functionσφ(x) are specified using deep neural networks.

---

2.3. Deep Latent Gaussian Models

In this paper, we study deep latent Gaussian models (DLGM), which are a general class of deep directed graphical models that consist of a hierarchy of L layers of Gaussian latent variables zl for layer l. Each layer of latent variables is dependent on the layer above in a non-linear way, and for DLGMs, this non-linear dependency is specified by deep neural networks. The joint probability model is:

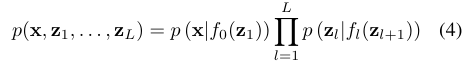
where the Lth Gaussian distribution is not dependent on any other random variables. The prior over latent variables is a unit Gaussian p(zl) = N (0, I) and the observation likelihood pθ(x|z) is any appropriate distribution that is conditioned on z1 and is also parameterized by a deep neural network (figure 2). This model class is very general and includes other models such as factor analysis and PCA, non-linear factor analysis, and non-linear Gaussian belief networks as special cases (Rezende et al., 2014).

 

DLGMs use continuous latent variables and is a model class perfectly suited to fast amortized variational inference using the lower bound (3) and stochastic backpropagation. The end-to-end system of DLGM and inference network can be viewed as an encoder-decoder architecture, and this is the perspective taken by Kingma & Welling (2014) who present this combination of model and inference strategy as a variational auto-encoder. The inference networks used in Kingma & Welling (2014); Rezende et al. (2014) are simple diagonal or diagonal-plus-low rank Gaussian distributions. The true posterior distribution will be more complex than this assumption allows for, and defining multimodal and constrained posterior approximations in a scalable manner remains a significant open problem in variational inference.

---

3. Normalizing Flows

By examining the bound (3), we can see that the optimal variational distribution that allows DKL[q||p] = 0 is one for which qφ(z|x) = pθ(z|x), i.e. q matches the true posterior distribution. This possibility is obviously not realizable given the typically used q(·) distributions, such as independent Gaussians or other mean-field approximations. Indeed, one limitation of the variational methodology due to the available choices of approximating families, is that even in an asymptotic regime we can not obtain the true posterior. Thus, an ideal family of variational distributions qφ(z|x) is one that is highly flexible, preferably flexible enough to contain the true posterior as one solution. One path towards this ideal is based on the principle of normalizing flows (Tabak & Turner, 2013; Tabak & VandenEijnden, 2010).

 

A normalizing flow describes the transformation of a probability density through a sequence of invertible mappings. By repeatedly applying the rule for change of variables, the initial density ‘flows’ through the sequence of invertible mappings. At the end of this sequence we obtain a valid probability distribution and hence this type of flow is referred to as a normalizing flow.

---

3.1. Finite Flows

The basic rule for transformation of densities considers an invertible, smooth mapping f : Rd → Rd with inverse f −1 = g, i.e. the composition g ◦ f(z) = z. If we use this mapping to transform a random variable z with distribution q(z), the resulting random variable z' = f(z) has a distribution:

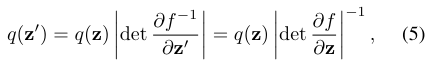
where the last equality can be seen by applying the chain rule (inverse function theorem) and is a property of Jacobians of invertible functions. We can construct arbitrarily complex densities by composing several simple maps and successively applying (5). The density qK(z) obtained by successively transforming a random variable z0 with distribution q0 through a chain of K transformations fk is:

where equation (6) will be used throughout the paper as a shorthand for the composition fK(fK−1(. . . f1(x))). The path traversed by the random variables zk = fk(zk−1) with initial distribution q0(z0) is called the flow and the path formed by the successive distributions qk is a normalizing flow. A property of such transformations, often referred to as the law of the unconscious statistician (LOTUS), is that expectations w.r.t. the transformed density qK can be computed without explicitly knowing qK. Any expectation EqK [h(z)] can be written as an expectation under q0 as:

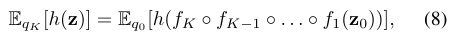
which does not require computation of the the logdetJacobian terms when h(z) does not depend on qK.

 

We can understand the effect of invertible flows as a sequence of expansions or contractions on the initial density. For an expansion, the map z' = f(z) pulls the points z away from a region in Rd , reducing the density in that region while increasing the density outside the region. Conversely, for a contraction, the map pushes points towards the interior of a region, increasing the density in its interior while reducing the density outside.

 

The formalism of normalizing flows now gives us a systematic way of specifying the approximate posterior distributions q(z|x) required for variational inference. With an appropriate choice of transformations fK, we can initially use simple factorized distributions such as an independent Gaussian, and apply normalizing flows of different lengths to obtain increasingly complex and multi-modal distributions.

---

4. Inference with Normalizing Flows

To allow for scalable inference using finite normalizing flows, we must specify a class of invertible transformations that can be used and an efficient mechanism for computing the determinant of the Jacobian. While it is straightforward to build invertible parametric functions for use in equation (5), e.g., invertible neural networks (Baird et al., 2005; Rippel & Adams, 2013), such approaches typically have a complexity for computing the Jacobian determinant that scales as O(LD^3), where D is the dimension of the hidden layers and L is the number of hidden layers used. Furthermore, computing the gradients of the Jacobian determinant involves several additional operations that are also O(LD^3) and involve matrix inverses that can be numerically unstable. We therefore require normalizing flows that allow for low-cost computation of the determinant, or where the Jacobian is not needed at all.

---

4.1. Invertible Linear-time Transformations

We consider a family of transformations of the form:

 

Not all functions of the form (10) or (14) will be invertible. We discuss the conditions for invertibility and how to satisfy them in a numerically stable way in the appendix.

---

7. Conclusion and Discussion

In this work we developed a simple approach for learning highly non-Gaussian posterior densities by learning transformations of simple densities to more complex ones through a normalizing flow. When combined with an amortized approach for variational inference using inference networks and efficient Monte Carlo gradient estimation, we are able to show clear improvements over simple approximations on different problems. Using this view of normalizing flows, we are able to provide a unified perspective of other closely related methods for flexible posterior estimation that points to a wide spectrum of approaches for designing more powerful posterior approximations with different statistical and computational tradeoffs.

 

An important conclusion from the discussion in section 3 is that there exist classes of normalizing flows that allow us to create extremely rich posterior approximations for variational inference. With normalizing flows, we are able to show that in the asymptotic regime, the space of solutions is rich enough to contain the true posterior distribution. If we combine this with the local convergence and consistency results for maximum likelihood parameter estimation in certain classes of latent variables models (Wang & Titterington, 2004), we see that we are now able overcome the objections to using variational inference as a competitive and default approach for statistical inference. Making such statements rigorous is an important line of future research.

 

Normalizing flows allow us to control the complexity of the posterior at run-time by simply increasing the flow length of the sequence. The approach we presented considered normalizing flows based on simple transformations of the form (10) and (14). These are just two of the many maps that can be used, and alternative transforms can be designed for posterior approximations that may require other constraints, e.g., a restricted support. An important avenue of future research lies in describing the classes of transformations that allow for different characteristics of the posterior and that still allow for efficient, linear-time computation.