[Gated PixelCNN] PixelCNN's Blind Spot

Introduction

PixelCNNs are a type of generative models that learn the probability distribution of pixels, that means that the intensity of future pixels will be determined by previous pixels. In this blogpost series we implemented two PixelCNNs and noticed that the performance was not stellar. In the previous posts, we mentioned that one of the ways to improve the model's performance was to fix the blind spot problem. So, in this post, we will introduce the concept of blind spot, discuss how PixelCNNs are affected, and present one solution for solving it - the Gated PixelCNN.

---

Blind Spot

As you recall from the previous posts, the PixelCNN learns the conditional distribution for all pixels in the image and uses this information to make predictions. Also recall that PixelCNNs will learn the distribution of the pixels from left to right and top to bottom. So to make sure that ‘future’ pixels (i.e., pixels to the right or below the pixel that is being predicted) cannot be used for the prediction of the given pixel, a mask is generally used (Figure 1A). As shown in Figure 1A, the mask zeros out the pixels ‘after’ the pixel currently being predicted, which corresponds to the pixel at the center of the mask. However, due to this choice, not all ‘past’ pixels will be used to compute the new point, and the loss of information will lead to the creation of blind spots.

 

To understand the blind spot problem, let’s look at Figure 1B. In Figure 1B, the dark pink point (m) is the pixel we want to predict, as it is at the center of the filter. Because we are using a 3x3 mask (1A.), pixel m depends on l, g, h, i. On the other hand, those pixels depend on previous pixels. For example, pixel g depends on f, a, b, c, and pixel i depends on h, c, d, e. From figure 1B, we can also see that despite coming before pixel m, pixel j is never taken into account to compute the predictions for m. Similarly, if we want to make predictions for q, j, n, o are never considered (Figure 1C.). The fact that not all previous pixels will influence the prediction is called the blind spot problem.

Figure 1: A. Illustrates an example of a 3x3 mask that can be used to make sure that only ‘past’ pixels are used to compute predictions. Only the pixels in green will be used to calculate the pixel in the centre of the mask. B. An example of how the mask can be used on a 5x 5 image to predict pixel m. Only the pixels l, g, h, i will be used to calculate the pixel in dark pink (m). However, we need to remember that l, g, h, i also depend on previous pixels (a, b, c, d, e, f, k; shown in lilac). It is visible from the third picture in B that j (in orange) will not be used, and thus form a blind spot. C. If we move the centre of the mask down to now predict pixel q, we can see how pixels in orange will never be taken into account (Image by author).

Looking at the receptive field (marked in yellow in Figure 2) of the original PixelCNN, we can see the blind spot and how it propagates over the different layers. In the second part of this blogpost, we will describe the next version of PixelCNN, the Gated PixelCNN, that introduces a new mechanism to avoid the creation of blind spots.

Figure 2: Evolution of the blind spot on the PixelCNN (Image by author).

---

Gated PixelCNN

In the last two blog posts, we introduced the PixelCNN; however, this model had low performance and suffered from the blind spot problem that we introduced above.

 

To solve these issues, van den Oord et al. (2016) introduced the Gated PixelCNN. The Gated PixelCNN differs from the PixelCNN in two major ways:

1. It solves the blind spot problem
2. It improves the model's performance using Gated Convolution Layers

---

1. How Gated PixelCNN solved the Blind Spot problem

This new model solved the blind spot issue by splitting the convolution into two parts: the vertical and horizontal stacks. Let’s look into how the vertical and horizontal stacks work.

Vertical and Horizontal Stacks

Figure 3: The vertical (in green) and Horizontal stack (in blue - Image by author).

In the vertical stack, the goal is to process the context information from all rows before the current one. The trick used to make sure that all previous information is used and that causality is kept (i.e., the currently predicted pixel should not be aware of the information to its right), is to shift the centre of the mask up by one row, respectively to the pixel being predicted. As illustrated in Figure 3, although the center of the vertical mask is the light green pixel (m), the information gathered by the vertical stack will not be used to predict it, but it will, instead, be used to predict the pixel in the row below it (r).

 

However, using the vertical stack alone would create blind spots to the left of the black predicted pixel (m). To avoid this, the information gathered by the vertical stack is combined with information from the horizontal stack (p-q represented in blue in Figure 3), which predicts all pixels to the left of the predicted pixel (m). The combination between the horizontal and vertical stack solves two problems: (1) no information on the right of the predicted pixel will be used, (2) because we take into consideration as a block, we no longer have a blind spot.

 

In van den Oord et al. (2016), the vertical stack is implemented so that the receptive field of each convolution has a 2x3 format. We implemented this by using a 3x3 convolution with the last row masked out. In the horizontal stack, the convolution layers associate the predicted value with the data from the current row of the pixel analysed. This can be implemented using a 1x3 convolution where we mask the future pixels to guarantee the causality condition of the autoregressive models. Similar to the PixelCNN, we implemented a type A mask (that is used in the first layer) and a type B mask (used in the subsequent layers).

 

By adding the feature maps of these two stacks across the network, we get an autoregressive model with a consistent receptive field and does not produce blind spots (Figure 4).

Figure 4: Overview of the receptive field for the Gated PixelCNN. We notice that using the combination of vertical and horizontal stacks we were able to avoid the Blind spot problem observed in the initial version of PixelCNNs (Figure 3 — Image by author).

---

2. The Gated activation unit (or gated blocks)

The second major improvement from the vanilla PixelCNNs to the Gated CNNs is the introduction of gated blocks and multiplicative units (in the form of the LSTM gates). Therefore, instead of using the rectified linear units (ReLUs) between the masked convolutions, like the original pixelCNN; Gated PixelCNN uses gated activation units to model more complex interactions between features. This gated activation units use sigmoid (as a forget gate) and tanh (as real activation). In the original paper, the authors suggested that this could be one reason PixelRNN (that used LSTM’s) outperformed PixelCNN as they are able to better capture the past pixels by means of recurrence — they can memorize past information. Therefore, Gated PixelCNN used the following:

 

σ is the sigmoid non-linearity, k is the number of the layer, ⊙ is the element-wise product, ∗ is the convolution operator, and W are the weights from the previous layer. Let’s look in more detail at a single layer in the PixelCNN.

---

Single layer block in a Gated PixelCNN

The stacks and gates are the fundamental blocks of the Gated PixelCNN (Figure 5). But how are they connected, and how will the information be processed? We will break this down into 4 processing steps, which we will discuss in the sessions below.

Figure 5: Overview of the Gated PixelCNN architecture (image from the  original paper ). The colours represent different operations (i.e., Green: Convolution; Red: element-wise multiplications and additions; Blue: Convolutions with the weights

---

1. Calculate the vertical stack features maps

(image adapted from the  original paper )

As a first step, the input from the vertical stack is processed by our 3x3 convolution layer with the vertical mask. Then, the resulting feature maps pass through the gated activation units and are inputted in the next block’s vertical stack.

---

2. Feeding vertical maps into horizontal stack

(image adapted from the  original paper )

For our autoregressive model, it is necessary to combine the information of both vertical and horizontal stacks. For this reason, in each block, the vertical stack is also used as one of the inputs to the horizontal layer. Since the centre of each convolutional step of the vertical stack corresponds to the analysed pixel, we cannot just add the vertical information. This would break the causality condition of the autoregressive models as it would allow information of future pixels to be used to predict values in the horizontal stack. This is the case on the second illustration in Figure 8A, where the pixels on the right (or future) of the black pixel are used to predict it. For this reason, before we feed the vertical information to the horizontal stack, we shift it down using padding and cropping (Figure 8B.). By zero-padding the image and cropping the bottom of the image, we can ensure that the causality between the vertical and horizontal stack is maintained. We will delve into more detail about how cropping works in future posts, so do not worry if its details are not completely clear.

Figure 8: How to ensure that the causality between the pixels are mantained (image by author)

---

3. Calculate horizontal feature maps

(image adapted from the  original paper )

In this step, we process the feature maps of the horizontal convolutional layer. In fact, the first step consists of summing the feature maps from the vertical to the outputs of the horizontal convolution layer. The output of this combination has the ideal receptive format, which considers the information of all previous pixels. Finally, the feature maps go through the gated activation units.

---

4. Calculate the residual connection on the horizontal stack

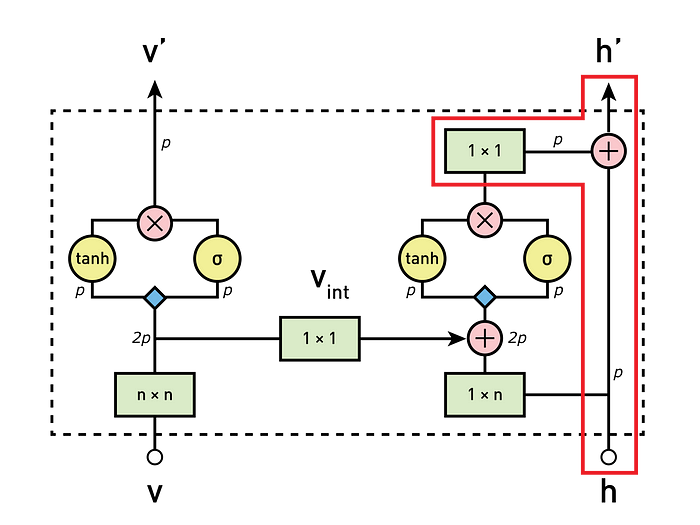
(image adapted from the  original paper )

In this last step, if the block is not the first one of the network, a residual connection will combine the output of the previous step (processed by a 1x1 convolution) and then fed into the horizontal stack of the next block. If it is the first block of the network, then there is no residual connection, and this step is skipped.

 

In summary, using the gated block, we solved the blind spots on the receptive field and improved the model performance.

---

Architecture

In Oord et al. 2016, the PixelCNN uses the following architecture: the first layer is a masked convolution (type A) with 7x7 filters. Then, 15 residuals blocks were used. Each block process the data with a combination of 3x3 layers convolutional layers with mask type B and standard 1x1 convolutional layers. Between each convolutional layer, there is a non-linearity ReLU. Finally, the residual blocks also included a residual connection.

 

In the next post, we will take a look at how to improve even further the performance of the Gated PixelCNN. We will also introduce the conditional PixelCNN, so stay tuned!

---

Results

We trained both a PixelCNN and a Gated PixelCNN and compare the results below.

Figure 11: A comparison between PixelCNN and Gated PixelCNN (Image by author)

When comparing the MNIST prediction for PixelCNN and Gated PixelCNN (Figure 11), we do not observe a great improvement for this dataset on the MNIST. Some of the numbers that were previously corrected predicted are now incorrectly predicted. However, this does not mean that PixelCNNs should not be taken into account.