-
Pixel Recurrent Neural NetworksResearch/Generative Model 2024. 5. 14. 08:19
Pixel-RNN presents a novel architecture with recurrent layers and residual connections that predicts pixels across the vertical and horizontal axes. The architecture models the joint distribution of pixels as a product of conditional distributions of horizontal and diagonal pixels. The model achieves state-of-the-art in the generation of natural images.
(…) we can conclude that the PixelRNNs are able to model both spatially local and long-range correlations and are able to produce images that are sharp and coherent. Given that these models improve as we make them larger and that there is practically.

Occluded version, predictions and original image by PixelRNN
Model

To generate pixel x_i one conditions on all the previously generated pixels Joint distribution: To estimate the joint distribution p(x) we can write it as the product of conditional distributions over pixels.

The model tries to predict a pixel’s color for a specific channel (RGB) given all previous predictions (previous pixels colors and other channels (RGB) already predicted for the target pixel). The authors modeled the distribution in a discrete manner (i.e. each channel value was an integer between [1–256]) since this was easier to learn and it performs better.
Row LSTM
Row LSTM processes the image row by row with a 1D convolution and captures a triangular area above the pixel, shown below:

State-to-state (top) and input-to-state (bottom) mappings in Row LSTM Note that the RNN has a triangular receptive field and thus is unable to capture all the relevant content. How does it work?
LSTM’s have a cell state which acts as an input to the next state (state-to-state) and a fresh input that modifies the current state (input-to-state). Within each cell the network has four activation functions which produce four gate vectors. In PixelRNN, the input-to-state component is first computed for the entire input map with a k x 1 sized convolution which goes row by row. The convolution is masked to include only previous pixels and produces a tensor of size 4h, n, n where h is the size of the output feature map, n is the image dimension and 4 is the number of gate vectors in the LSTM cell. Then the state-to-state component is computed by applying a convolution to the previous state.

State-to-state 
Input-to-state
Diagonal BiLSTM
This new architecture computes convolutions in a diagonal fashion.
Each of the two directions of the layer scans the image in a diagonal fashion starting from a corner at the top and reaching the opposite corner at the bottom.
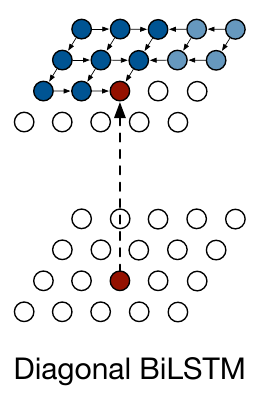
State-to-state (top) and input-to-state (bottom) mappings in Diagonal BiLSTM It is computed by first skewing the input map into a new map with each row offset by one pixel with respect to the previous one. The final size of the new input map is n x *(2n-1).

Pixel offset to perform diagonal convolutions For each of the two directions, the input-to-state component (1x1 convolution) is computed. The state-to state component is computed with a column-wise convolution with kernel size (2x1). The output feature map is squeezed back into n x n dimensions.
Two advantages of this architecture are that it has a complete dependency field and that by using a large number of small computations (2x1 kernel) it yields a highly non-linear computation (notice that each new pixel that is predicted is a new input to the network and undertakes several non-linear operations before it can affect the cell state).
The model has residual connections from one layer to the next with a structure that can be seen in the next image.

Residual layers within the cells of the LSTM
Masked Convolutions
Masks are necessary to prevent the network from using some information to predict a pixel.
The h features for each input position at every layer in the network are split into three parts, each corresponding to one of the RGB channels. When predicting the R channel for the current pixel xi , only the generated pixels left and above of xi can be used as context. When predicting the G channel, the value of the R channel can also be used as context in addition to the previously generated pixels. Likewise, for the B channel, the values of both the R and G channels can be used.
The authors used 2 masks for their different layers, Mask A and Mask B. Mask A is applied to the first convolutional layer in a PixelRNN and restricts the connections to the previous pixels and to colors that have already been predicted. Mask B is applied to all input-to-state convolutional transitions and allows the connection of a color to itself.

Mask A and Mask B. Their difference is that Mask B allows colors to connect with themselves. 
Where is each mask used. Mask A is used in the first layer and mask B in all input-state convolutions
PixelCNN
The Row and Diagonal LSTM layers have a potentially unbounded dependency range within their receptive field.
This means that each pixel could potentially be using information from every pixel before itself.
This comes with a computational cost as each state needs to be computed sequentially.
An alternative to this is to use standard, bounded convolutions in a non-sequential manner. This allows to compute every pixel at once, in parallel (since it is not sequential) while training or evaluating (when generating you need every previous pixel to generate the next one). Enter PixelCNN.
The PixelCNN uses multiple convolutional layers that preserve the spatial resolution; pooling layers are not used. Masks are adopted in the convolutions to avoid seeing the future context.

State-to-state (top) and input-to-state (bottom) mappings in Pixel CNN
Multi-Scale PixelRNN
Multi-Scale PixelRNN is composed of an unconditional PixelRNN and one or more conditional PixelRNN’s. The unconditional network first generates in the standard way a smaller s x s image that is subsampled from the original image. The conditional network then takes the s x s image as an additional input and generates a larger n x n image.

Results
The model achieved state-of-the-art performance in MNIST and CIFAR10. As you can see, Diagonal BiLSTM (the model with the largest receptive field) achieved the lowest loss. This suggests that having a high receptive field is important to increase performance.

Negative log-likelihood in MNIST 
Test-set performance for CIFAR10 in bits/dim Let’s get to the examples. Below we can see the samples (created by training in ImageNet) generated by the standard and multi-scale PixelRNN’s. If we look at them carefully, the pictures on the right seem globally more coherent (some sort of structure in the image, closer to a real image). This suggests that multi-scale models are better at preserving global coherence than standard PixelRNN’s.

Left: normal model, Right: multi-scale model. 'Research > Generative Model' 카테고리의 다른 글
[Gated PixelCNN] PixelCNN's Blind Spot (0) 2024.05.14 Pixel Recurrent Neural Networks (0) 2024.05.14 What is a variational autoencoder? (0) 2024.05.11 Variational autoencoders (0) 2024.05.10 Understanding Generative Adversarial Networks (GANs) (0) 2024.05.05