-
SST: Multi-Scale Hybrid Mamba-Transformer Experts for Long-Short Range Time Series ForecastingNLP/NLP_Paper 2024. 9. 25. 00:13
https://arxiv.org/pdf/2404.14757
머리 속에 그리고 있던 이상적인 형태의 연구가 그대로 논문으로 실현되어서 정말 너무너무 놀랐다.
내가 생각하던 Mamba와 Attention의 특장점을 제대로 살리면서, 그리고 내가 고민하던 부분 - "어떻게 합칠 것인가" (hybrid 형태)에 대한 solution을 기발하게 잘 제시했다.
즉, mamba - SSM이 time series의 장기적으로 stationary한 형태를 포착해나가는 특성 / attention이 국지적인 pattern을 잡아내는 특성을 제대로 조합했다.
그런데 여기서 "hybrid (조합)" 한다는 게 말은 멋있지만, 사실 구체적으로 방법을 생각하면 쉽지 않은데, 대다수의 SSM과 Transformer를 결합한 연구들을 보면, layer을 섞어놓는 형태인데, 나는 이게 진정한 의미의 hybrid라고 여겨지지가 않았다..
내가 왜 그런 생각이 들었냐면은..
예를 들어서, S6와 attn을 hierarchical하게 쌓는다고 하면, 만약 S6 layer을 통과한 후에 attn layer를 만난다면, 이미 S6의 관점에서 filter out된 정보에 attn을 하는 건데, 그렇다면 attn의 능력을 온전히 발휘할 수 없는 거잖아. 마찬가지로 attn 를 거친 후에 S6 layer를 만난다면, 역시 attn의 관점을 이미 거쳐온 input에 S6 layer를 적용하는 거고.
이게 nonsense라는 거는.. SSM과 attn이 가진 철학(지향하는 바)가 완전히 다르다는 걸 조금만 생각해보아도 바로 알 수가 있다.
SSM은 seq가 가진 내재적인 stationary 형태를 optimal 하게 approximate하는 것인데, attn으로 contextualize한 후(shuffle된) 후에 적용하겠다는 건 nonsense라고 느껴진다.. (my opinion!)
아무튼, 요약하자면!
각자가 가진 독립적인 힘을 온전히 발휘한 후 합쳐지는 게 아니잖아.
그래서..
뭔가 더 좋은 방법이 있을 것 같은데, 그게 뭘까..? 이게 나중 연구 주제가 되겠다.. 막연하게 keep해놓고 있었는데..
본 논문에서는
MoE로 아주 적절히 잘 섞었다!!!!! ㅎㅎ
아 어떡하지.. 이 논문.. 최근 내 머릿 속을 한동안 지배하던 완전 이상적인 형태의 현현인데..?
이상형 만난 것처럼 막 가슴이 두근두근거리네.
얼른 코드도 만나보고 싶다.
지금 너무 피곤해서..내일 다시 꼼꼼히 읽고, 코드 돌려봐야지..
참신한 architecture를 제시한 것 만으로도 넘나 영감을 팍팍 주고, thanks a lot인데, 심지어 performance도 좋다니....ㅜㅜ
사랑합니다.
아이디어가 상당히 명료하고, 각 component가 담당하는 역할이 분명하다. architecture가 직관적이고 모호함이 하나도 없기 때문에, code도 깔끔할 것 같다. 모듈화 잘 해놨을 것 같음 ㅎㅎ 안 봐도 비디오 ㅎㅎ "이거슨 컴싸 전공자들의 코드입니다"를 팍팍 풍기고 있을 듯 ㅎㅎㅎ
(archive에 올라온지 얼마 안된 논문이라 그런지, 중간에 경미한 오타가 있는 건, 읽으면서 내 블로그에는 수정해놓았다.)
Abstract
Despite significant progress in time series forecasting, existing forecasters often overlook the heterogeneity between long-range and short-range time series, leading to performance degradation in practical applications. In this work, we highlight the need of distinct objectives tailored to different ranges. We point out that time series can be decomposed into global patterns and local variations, which should be addressed separately in long- and short-range time series. To meet the objectives, we propose a multi-scale hybrid Mamba-Transformer experts model STATE SPACE TRANSFORMER (SST). SST leverages Mamba as an expert to extract global patterns in coarse-grained long-range time series, and Local Window Transformer (LWT), the other expert to focus on capturing local variations in fine-grained short-range time series. With an input-dependent mechanism, State Space Model (SSM)-based Mamba is able to selectively retain long-term patterns and filter out fluctuations, while LWT employs a local window to enhance locality-awareness capability, thus effectively capturing local variations. To adaptively integrate the global patterns and local variations, a long-short router dynamically adjusts contributions of the two experts. SST achieves superior performance with scaling linearly O(L) on time series length L. The comprehensive experiments demonstrate the SST can achieve SOTA results in long-short range time series forecasting while maintaining low memory footprint and computational cost. The code of SST is available at https://github.com/XiongxiaoXu/SST.
1. Introduction
Time series forecasting is a crucial problem in a wide range of real-world scenarios, including weather forecasting (Abhishek et al. 2012), stock prediction (Sezer, Gudelek, and Ozbayoglu 2020), and scientific computing (Xu et al. 2023). In scientific computing, for instance, ML-based surrogate models are trained to accelerate simulations of supercomputers by predicting their high-performance computing (HPC) behaviors over various timescales (Cruz-Camacho et al. 2023). Despite its importance, the lack of distinction between long-range and short-range time series largely hinders the performance of existing forecasters. Figure 1 shows different statistics of supercomputers, including network traffic of a port on a router, execution time of a HPC application, and busy time of a port on the router, change over time. These time series can be decomposed into global patterns in long range, such as repeated up-and-down trends, and local variations in short range, like extreme spike points. For long-range time series, it is essential to focus on global patterns, as local deviations, including outliers, can negatively impact forecasting accuracy. Conversely, short-range forecasting should emphasize local variations, because global patterns are less evident within limited time frames. Take the execution time for example. Extreme long execution times caused by sudden network congestion indicates an abnormal state in long-term trends but are pivotal for accurately forecasting next-term behaviors (Xu et al. 2024).
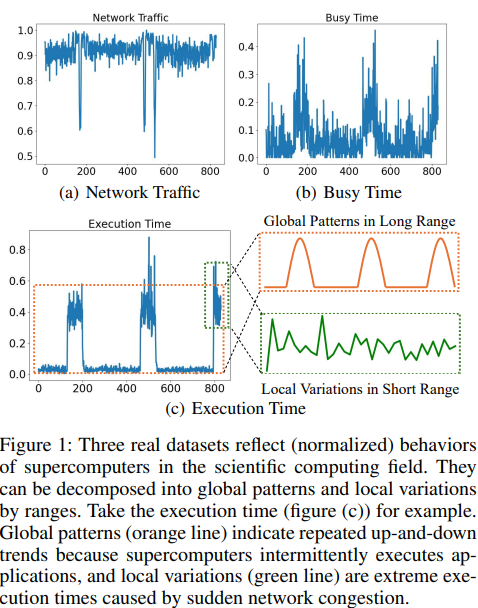
However, long-short range forecasting presents significant challenges. First, the distinction between long- and short-range time series remains ambiguous despite well-defined objectives: global patterns in long term, and local variations in short term. There is a pressing need for a strategy to differentiate them and a new metric to measure the difference. Second, both long- and short-range time series intertwine patterns and variations. It is often unclear how to only capture long-term patterns and filter out variations in long range while accurately depicting local deviations in short range. Third, integrating long- and short-range dependencies is a non-trivial task. It requires a model to adaptively learn the relative importance between patterns and variations, ensuring enhanced performance.
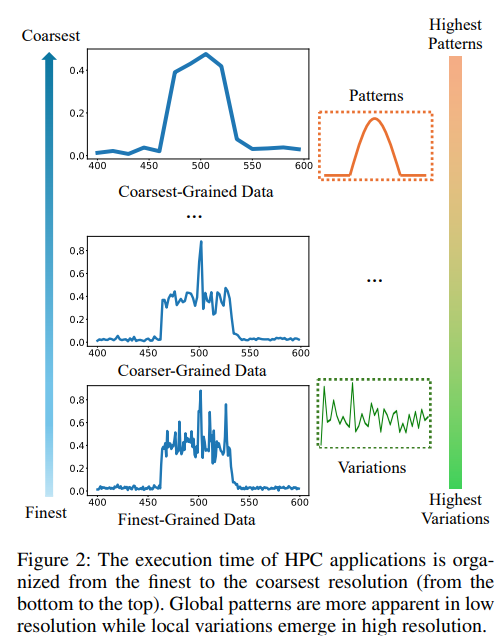
To address the first challenge, we propose a multi-resolution framework by incorporating patches (Nie et al. 2023) to adjust resolutions of time series. The resolution plays an important role in time series forecasting (Nie et al. 2023; Liu et al. 2021; Zhang et al. 2023). For example, patching techniques (Nie et al. 2023) can aggregate time steps into subseries patches to enhance the receptive field, and become increasingly popular in time series analysis. However, existing forecasters often apply the same patching or equally the same resolution to both long- and short-range time series, resulting in suboptimal performance. Figure 2 plots the shape of execution time varies with different resolutions. It demonstrates patterns are more discernible at a coarser granularity, while variations emerge at a finer granularity. To exploit the observations, we leverage the patching to distinguish long- and short-range time series. In specific, we employ larger patches and longer stride for long range to obtain low-resolution patched time series (PTS); smaller patches and shorter stride for short range lead to high-resolution PTS. Moreover, despite early promising results of patching, existing literature lacks methods to quantitatively assess the resolution of PTS. Therefore, we propose a novel metric to precisely quantify the resolution of PTS.
To solve the second and third challenges, we propose a novel hybrid Mamba-Transformer experts architecture, inspired by the idea of Mixture-of-Experts (MoEs) (Jacobs et al. 1991; Shazeer et al. 2017; Fedus, Zoph, and Shazeer 2022). Unlike traditional MoEs’ approaches where the roles of experts are ambiguous, we clearly delineates the responsibilities: Mamba serves as a global patterns expert to represent long-range dependencies, while Local Window Transformer (LWT) acts as a local variations expert to focus on short-range representations. As a representative State Space Model (SSM), Mamba is able to indefinitely retain relevant information in a manner dependent on the input with linear complexity (Gu and Dao 2023). This selective mechanism allows Mamba to preserve essential long-term patterns and disregard transient fluctuations. Meanwhile, LWT is specifically designed to focus on tokens within a local sliding window. The local window provides local inductive biases for vanilla Transformer, leading to enhanced local recognition capability, and reduces complexity from quadratic to linear. To seamlessly integrate the two specialized experts, a long-short router is proposed to adaptively learn their contributions. Remarkably, the hybrid architecture ensures a linear complexity O(L) on time series length L, benefiting from the hardware-aware algorithm in Mamba and the local window mechanism in LWT.
We term the proposed multi-scale hybrid Mamba-Transformer experts model as STATE SPACE TRANSFORMER (SST). To the best of our knowledge, SST is a very early attempt to build a hybrid Mamba-Transformer architecture in time series. Our contributions are summarized:
* We propose to decompose time series into global patterns and local variations according to ranges. We identify that global patterns as the focus of long range and local variations should be captured in short range.
* To effectively capture long-term patterns and short-term variations, we leverage the patching to create coarser PTS in long range and finer PTS in short range. Moreover, we introduce a new metric to precisely quantify the resolution of PTS.
* We propose a novel hybrid Mamba-Transformer experts architecture SST, with Mamba as a global patterns expert in long range, and LWT as a local variations expert in short range. A long-short router is designed to adaptively integrate the global patterns and local variations. With Mamba and LWT, SST is highly scalable with linear complexity O(L) on time series length L.
2. Related Work
Time Series Forecasting
Time series forecasting has been an crucial problem (Bontempi, Ben Taieb, and Le Borgne 2013; Xu 2023) for a long time. RNN (Cheng et al. 2018; Hewamalage, Bergmeir, and Bandara 2021) and LSTM (Yao et al. 2019; Xu et al. 2024) are two classical deep learning models for time series, but they fall short into gradient vanishing issues (Tetko, Livingstone, and Luik 1995) when dealing with long-range sequences. Inspired from the success of Transformer (Vaswani et al. 2017) in text data, a wide range of variants of Transformer (Wen et al. 2023; Li et al. 2019; Zhou et al. 2021; Liu et al. 2021; Wu et al. 2021; Zhou et al. 2022; Nie et al. 2023; Liu et al. 2024b) have proven effective in time series data. The latest iTransformer (Liu et al. 2024b) that simply applies the attention and feed-forward network on the inverted dimensions achieve SOTA performance. Recently, large language models (LLMs) are utilized for time series forecasting (Jin et al. 2023; Gruver et al. 2024; Tan et al. 2024) to explore potential of large foundation model. However, they ignore the heterogeneity of long- and short-range time series data and remain computationally challenging.
State Space Models and Mamba
State Space Models (SSMs) (Gu et al. 2021; Gu, Goel, and Re 2022; Gu and Dao 2023) emerge as a promising class of architectures for sequence modeling. With selective SSMs and a hardware-efficient algorithm, Mamba has achieve impressive performance across modalities such as languages (Gu and Dao 2023; Dao and Gu 2024), images (Zhu et al. 2024; Tang et al. 2024), medicine (Ma, Li, and Wang 2024; Xing et al. 2024), graph (Wang et al. 2024a; Behrouz and Hashemi 2024), recommendation (Liu et al. 2024a; Yang et al. 2024), and time series (Ahamed and Cheng 2024; Wang et al. 2024b; Patro and Agneeswaran 2024; Liang et al. 2024). A noteworthy line of research is to integrate Mamba and Transformer for the purpose of language modeling (Lieber et al. 2024; Park et al. 2024). A comparative study (Park et al. 2024) shows Mambaformer is effective in in-context learning tasks. Jamba (Lieber et al. 2024) is a production-grade attention-SSM hybrid model with 52B total available parameters for long context modeling. Different from the above hybrid models in text data, we first propose a hybrid Mamba-Transformer architecture SST in time series.
3. Preliminaries
Problem Statement
In the long-short range time series forecasting, historical time series with a look-back window L = (x1, x2, .., xL) ∈ R L×M with length L are given, where each xt ∈ R^M at time step t is with M variates. Long-range time series L denotes the full range of look-back window L[:], and short-range time series S ∈ R S×M denotes the partial latest range L[−S :], S < L. We aim to forecast F future values F = (xL+1, xL+2, .., xL+F ) ∈ R F ×M with length F.
State Space Models
The State Space Model (SSM) is a class of sequence modeling frameworks that are broadly related to RNNs, and CNNs, and classical state space models (Gu et al. 2021). They are inspired by a continuous system that maps an input function x(t) ∈ R to an output function y(t) ∈ R through an implicit latent state h(t) ∈ R N as follows:

where A ∈ R N×N , B ∈ R N×1 , and C ∈ R 1×N are learnable matrices. SSM can be discretized from continuous signal into discrete sequences by a step size ∆ as follows:

The discrete parameters (A_bar, B_bar) can be obtained from continuous parameters (∆, A, B) through a discretization rule, such as zero-order hold (ZOH) rule A_bar = exp(∆A), B_bar = exp(∆A) −1 (exp(∆A) − I) · ∆B. After discretization, the model can be computed in two ways, either as a linear recurrence for inference as shown in Equation 2, or as a global convolution for training as the following Equation 3 where K_bar is a convolution kernel:

S4 is a structured SSM where the specialized Hippo (Gu et al. 2020) structure is imposed on the matrix A to capture long-range dependency. Building upon S4, Mamba (Gu and Dao 2023) incorporates a selective SSM to propagate or forget information along the sequence, and a hardware-aware algorithm for efficient implementation.
Motivating Examples for Mamba and Transformer
Mamba and Transformer process data in different ways.
Mamba
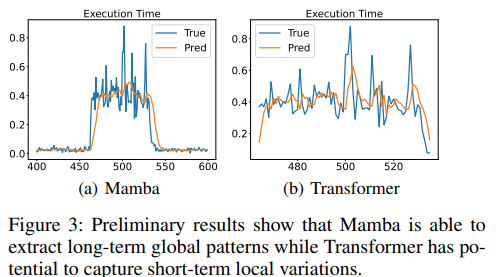
parameterizes the SSM’s parameters based on inputs, which enables it selectively focus on or ignore particular inputs. With a RNN-like hidden state, Mamba selectively stores global patterns into the hidden state and forgets irregular fluctuations. It motivates us to adopt Mamba extract global patterns in time series. The preliminary result in Figure 3(a) demonstrates Mamba can retain repeated up-and-down patterns in long range. Furthermore, linear complexity allows Mamba easily scale to long-range time series.
Transformer,
instead of maintaining a hidden state, adopts attention mechanism to directly access to past tokens and acquire dependencies. Such straightforward message-passing method facilitates depicting variations of data. The previous literature (Zeng et al. 2023) indicates Transformer easily adapts to sudden change noises, which aligns with our intuition. It motivates us to leverage Transformer to depict local variations. Figure 3(b) shows Transformer has potential to capture irregular fluctuations. However, two shortcoming exist for Transformer: (1) the missing local inductive bias hinders its ability to further capture local variations; (2) quadratic complexity of vanilla attention limits its scalability. We will later address the two issues with a local window.
4. Methodology
As shown in Figure 4, SST (STATE SPACE TRANSFORMER) includes four modules: multi-scale patcher, global patterns expert, local variations expert, and long-short router. Multi-scale patcher transforms input time series (TS) into different resolutions according to ranges. Based on multi-scale TS, a global pattern expert is dedicated to finding long-term patterns in a low-resolution TS, and a local variations expert aims to capture short-term variations in a high-resolution TS. Finally, a long-short router dynamically learns contributions of the two experts.

Multi-Scale Resolutions
Patching.
As shown in Figure 2, global patterns emerge when viewed at a broader-scale granularity, while local variations become clearer when examined at a finer-scale granularity. Consequently, we propose a multi-scale pacther to differentiate long- and short-range TS by providing them with distinct resolutions. i.e., low resolution for long-range TS and high resolution for short-range TS. In detail, the patcher modifies resolutions by aggregating a series of time steps into patches and independently operates patching for individual channels (Nie et al. 2023). Formally, input TS
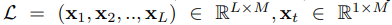
is divided into M univariate time series


The patching process involves two factors: the patch length P and the stride length Str (the interval between the end point of two consecutive patches). Accordingly, the number of patches is
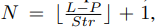
and the patcher for each variate x^(i) generates a sequence of patches x^(i)_p ∈ R N×P , named patched time series (PTS). Note that for unpatched TS x^(i) ∈ R L×1 , L is the sequence dimension and 1 denotes the variate dimension. Correspondingly, for PTS x^(i)_p ∈ R N×P , N is the new sequence dimension and P is the new variate dimension.
Resolution.
Intuitively, larger patches P, longer stride Str, and accordingly less number of patches N indicates a low resolution. We adopt such setting to generate a low resolution TS for long range. It allows SST focus on modeling long-term global patterns and ignoring small fluctuation. By contrast, smaller patches and shorter stride imply a high resolution. It enables SST to depict short-term nuances. Although the patching is becoming popular in TS community, no existing work tries to quantify resolutions of PTS. To mitigate the gap, we define a new metric as follows:
Definition 1.
PTS (Patched Time Series) Resolution. Let P, Str, and N denote patch length, stride length, and number of patches for a patched time series. The resolution of a PTS is defined as R_PTS = √ P / Str .
The definition of PTS resolution takes two factors into account. First, PTS resolution aims to quantify the relative granularity of a PTS compared to its unpatched one. Second, PTS resolution describes the amount of temporal information of a PTS, in both the sequence dimension and variate dimension. Similar to the definition of the image resolution (Boellaard et al. 2004) equaling to |width| × |height|, we multiply the two dimensions of PTS, but with a penalized root at variate dimension, i.e., |sequence| × √ |variate| because we focus more on the sequence (temporal) dimension of PTS. For example, after an univariate TS x^(i) ∈ R L×1 is patched into a PTS x^(i)_p ∈ R N×P where N is at the new sequence dimension, and P is at the new variate dimension, the PTS resolution R_PTS is defined as:

With the definition, an unpatched TS x^(i) ∈ R 1×L can be regarded as a PTS with R_PTS = 1 (patch length P = 1 and stride length Str = 1). The multi-scale patcher processes long-range TS with a low R^L_PTS, and obtains x^(i)_pL ∈ R N_L×P_L . Conversely, the patcher handle short-range TS with a relatively high R^S_PTS, and outputs
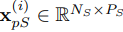
Hybrid Mamba-Transformer Experts
Inspired by Mixture-of-Experts (MoEs) (Jacobs et al. 1991; Shazeer et al. 2017; Fedus, Zoph, and Shazeer 2022), we introduce a hybrid Mamba-Transformer experts architecture. Unlike ambiguous roles in traditional MoEs models, we assign global patterns and local variations roles to two experts.
Global Patterns Expert.

Mamba achieves impressive performance on tasks requiring scaling to long-range sequences as it introduces a selective mechanism to remember relevant patterns and filter out irrelevant noises indefinitely. Consequently, we incorporate the Mamba block as a expert to extract long-term patterns and filter out small variations in long-range TS. As shown in Figure 4, the global patterns expert encodes long-range PTS
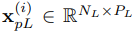
into high-dimension space

in the encoding layer, and a Mamba block is followed. Mamba takes an input x^(i)_L and expands the dimension by two input linear projections. For one projection, Mamba processes the expanded embedding through a convolution and a SiLU activation before feeding into the SSM. The core discretized SSM module is able to select input-dependent patterns and filter out irrelevant variations. The other projection followed by SiLU activation, as a residual connection, is combined with output of the SSM module through a multiplicative gate. Finally, Mamba delivers output
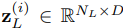
through an output linear projection.
Note that we do not need a positional embedding typically existing in Transformer as Mamba’s recurrence mechanism (Gu et al. 2021) naturally encodes positions.
Local Variations Expert.
Transformer is potential to capture variations as discussed in the Section 3, but lack of locality inductive bias and quadratic complexity impacts its adoption. Therefore, we propose local window Transformer (LWT) with enhanced locality-awareness capabilities to capture local variations in short range. Figure 4 shows the local variations expert first projects short-range PTS

and positional information into a embedding

The embedding is fed into LWT where the local window attention forces each token only attends to surrounding tokens within the window. In a formal way, for a fixed window size w, each token only attends to 1/2 w surrounding tokens on two sides. After input embedding x^(i)_S is projected into query Q, key K, and value V in each head, LWT calculates attention scores between tokens within the w window size as follows:
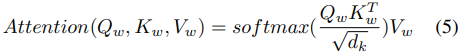
where Q_w, K_w, and V_w denote query, key, and value vector within the local window, 1/√ dk is used to avoid extremely small gradients (Vaswani et al. 2017) and d_k is the dimension of V_w. The output of multiple heads are concatenated and then projected back into the D-dimension space. We denote output of LWT as
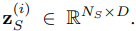
Figure 5 illustrates the mechanism of local window attention. Despite its strong local inductive bias, LWT maintains an extensive receptive field. By stacking multiple layers, the upper layers gain access to all input locations, enabling the construction of representations that integrate information across the entire input, similar to the capabilities of CNNs (Wu et al. 2019). The LWT is able to increase the receptive field by stacking multiple layers, and the respective field of layer l is l × w.
Moreover, the computation complexity of this pattern reduce from O(S^2) to O(w∗S) on the length of short-range TS (not considering the patching).

Mixture of Experts
Long-Short Router.
In the MoE community, router (Fedus, Zoph, and Shazeer 2022) is a key module which primarily directs tokens to only a subset of experts for saving computational cost. Different from the path-assigning role of traditional MoE routers, the proposed long-short router is capable of learning the relative contributions of the two specialized experts, adaptively integrating long- and short-range TS representations. Formally, the router projects input TS L ∈ R L×M into the D-dimension space, subsequently transformed by a flatten layer into a vector z_R. A linear layer with a softmax function is followed to output two values p_L, p_S ∈ (0, 1), indicating two weights of the global patterns and the local variations experts.
Forecasting Module.
The forecasting module flattens long-range embedding z^(i)_L and short-range embedding z^(i)_S into a single-row vector and concatenates them with respective weights p_L and p_S. The resulting long-short range fusion representation

integrates long-term global patterns and short-term local variations information. Finally, a linear head is employed to forecast


for individual variate i.
Linear Complexity Analysis
SST maintains a linear complexity O(L) on input TS length L or

The high efficiency allows SST to avoid prohibitive computational complexity and memory usage, scaling to long time series. In detail, the complexity SST comes form two parts: Mamba and LWT. Mamba utilizes kernel fusion to reduce the amount of memory IOs and scan operation for parallel computation (Gu and Dao 2023) in the training, and adopts RNN-like mechanism in the inference, leading to a linear complexity O(L) on long-range TS L. Given self-attention operation occupies O(w^2) complexity within a local window with fixed-size w each step, LWT consumes O(w^2 ∗ S / w) complexity on short-range TS S. Considering the use of multi-scale patcher, the total complexity of SST is

Note that w, N_S, and N_L are constant, and S is linear related to and smaller than L.
5. Experiments
Experimental Setup
Datasets.
To evaluate the proposed SST (STATE SPACE TRANSFORMER), we adopt seven popular real-world datasets (Liu et al. 2024b), including ETTh1&ETTh2, ETTm1&ETTm2, Weather, ECL, and Traffic. The description of datasets are in the Appendix.
Baselines and Metrics.
We compare SST with time series forecasting methods within three years, including SMamba (Wang et al. 2024b), TimeMachine (Ahamed and Cheng 2024), iTransformer (Liu et al. 2024b), RLinear (Li et al. 2023), PatchTST (Nie et al. 2023), Crossformer (Zhang and Yan 2022), TimesNet (Wu et al. 2022), Dlinear (Zeng et al. 2023), FEDformerr (Zhou et al. 2022). Note that it is unfair to include LLMs approaches as they are pre-trained on a large corpus of data. To assess the performance of time series forecasters, we adopt two widely-used metrics MSE and MAE (Liu et al. 2024b). The lower MSE and MAE indicate more accurate forecasting results.
Experimental Setting.
We use low-resolution R_PTS = 0.43 (P_L = 48 and Str_L = 16) for long-range time series and high-resolution R_PTS = 0.5 (P_L = 16 and Str_L = 8) for short range. We set the look-back window length L = 2S = 672, and the future values length F ∈ {96, 192, 336, 720}. The experimental setting of baselines follows the latest SOTA iTransformer (Liu et al. 2024b).
Time Series Forecasting Results
We conduct multivariate time series forecasting experiments and results are shown in Table 1. It shows that SST achieves superior performance compared to baselines, including Mamba-based and Transformer based methods, across all real-world datasets. For example, compared to the S-Mamba, Mamba-based forecaster, and iTransformer, Transformer-based forecaster, SST reduces MSE error by 13.75% and 14.45% for the longest forecast length F = 720 on the ETTm1 dataset. The impressive performance benefits from the reasonable design of SST. Based on different granularity, SST employs a Mamba-based global patterns expert and a LWT-based local variations expert for long- and short-range time series. A following long-short router adaptively fuses long- and short-range dependencies, thus facilitating time series forecasting.

Ablation Studies
We conduct ablation study by excluding key components of SST and comparing SST with Mambaformer family.
Exclusion of Key Components.
To verify the effectiveness of each key component of SST, including global patterns expert, local variations expert, multi-scale patcher, and long-short router, we design an ablation study on variants: Mamba, LWT, w/o Patcher (SST without the Patcher), w/o Router (SST without the Router) as shown in Figure 6(a). Accordingly, we have the following observations: (1) SST achieves impressive performance compared to Mamba and LWT. The reason is that SST can integrate strengths of Mamba and Transformer, thus effectively capturing global patterns in long range and local variations in short range. It demonstrates the effectiveness of hybrid Mamba-Transformer architecture in SST. (2) Compared to w/o Patcher and w/o Router, SST obtains superior performance. It is because the multi-scale patcher can patch long and short-range TS in distinct resolutions, thus facilitating feature extraction of two experts; the long-short router can dynamically learn contributions of the two experts. It verifies reasonable design of multi-scale framework and MoE architecture in SST.

Comparison with Mambaformer Family.
Given SST is the first hybrid Mamba-Transformer model in time series, we are interested in if the method to integrate Mamba and Transformer in SST is the optimal. To answer the question, we adapt the Mambaformer family (Park et al. 2024), which is originally developed for language modeling, to time series. Mambaformer family attempts to combine strengths of Mamba and Transformer by directly interleaving Mamba and attention layers. In particular, the Mambaformer family consists of: Mambaformer where a pre-processing Mamba block is followed by interleaved Attention-Mamba layers, Attention-Mamba where interleaved Attention-Mamba layers are utilized, Mamba-Attention where interleaved Mamba-Attention layers are employed. More details are shown in Appendix. The results are displayed in Figure 6(b). It shows that Mambaformer family cannot reach desirable performance compared to SST. It implies that directly interleaving Mamba and attention cannot fully unleash potential of hybrid architectures. The more careful and specific design for time series like SST is necessary.
Memory and Speed Analysis
To check the efficiency of SST in practice, we conduct memory and speed analysis. As shown in Figure 7, we depict figures where consumed memory and the elapsed time each epoch vary with the length of input TS L. We compare SST with PatchTST (Nie et al. 2023) and vanilla Transformer (Vaswani et al. 2017). Note that we do not compare iTransformer because its attention operates on variate dimension instead of sequence dimension. All the computations were performed on 24 GB NVIDIA RTX A5000 GPU at Ubuntu 20.04.6 LTS. From the figure, we observe SST is efficient and has promising scalability on time steps. SST is able to scale linearly to 6k time steps. The impressive scalability stems from the fact that Mamba implement a hardware-aware algorithm, and LWT leverages a fixed-size sliding window to operate attentions. In contrast, vanilla Transformer struggles in quadratic complexity, significantly preventing it from attending to long time series. In the experiments, vanilla Transformer can only attend to maximum 336 time steps. It cannot continue increasing input length due to the OOM (Out-Of-Memory) issue. PatchTST uses patch techniques to reduce complexity by a factor of stride, thus alleviating the issue to a degree. However, it still fall short of scalability and can only scale to 3k time steps, much lower than 6k time steps of SST. The memory and speed analysis demonstrate efficiency of SST in practice.

6. Concluison and Future Work
In this paper, we point out that time series can be decomposed into global patterns and local variations based on ranges. Global patterns should be extracted from long range, while local variations are more effectively captured in short range. To this end, we introduce a multi-scale hybrid Mamba-Transformer framework SST. Specifically, Mamba, serving as a global patterns expert, focuses on extracting long-term patterns in low resolution. Conversely, LWT, as a local variations expert, addresses subtle nuances in short-range time series in high resolution. To adaptively integrate the two experts, a long-short router dynamically learn contributions of Mamba and LWT. SST exhibits high efficiency with scaling linearly O(L) with time series length L. Comprehensive experiments across seven real-world datasets demonstrate SST achieves superior forecasting performance while maintaining low memory usage and high computation speed. The future work includes exploring hybrid Mamba-Transformer architectures in other time series analysis, such as classification and anomaly detection.
7. Appendix
Datasets
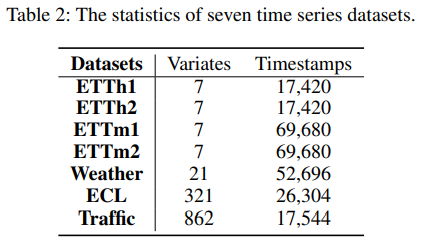
The seven widely-used real-world datasets (Liu et al. 2024b) in the experiments, consisting of, ETTh1&ETTh2, ETTm1&ETTm2, Weather, ECL, and Traffic, are summarized in Table 2. The detailed description of the seven realworld datasets are as follows:
• ETT dataset (Zhou et al. 2021) includes data on seven factors related to electricity transformers, spanning from July 2016 to July 2018. It consists of four subsets: ETTh1 and ETTh2, recorded hourly, and ETTm1 and ETTm2, recorded every 15 minutes.
• Weather dataset (Wu et al. 2021) captures 21 meteorological factors, recorded every 10 minutes by the Weather Station at the Max Planck Institute for Biogeochemistry throughout 2020.
• ECL dataset (Wu et al. 2021) offers hourly electricity consumption data from 321 clients.
• Traffic dataset (Wu et al. 2021) contains hourly road occupancy rates collected by 862 sensors across the San Francisco Bay Area freeways, covering the period from January 2015 to December 2016.
Implementation Details
All experiments are performed on 24 GB NVIDIA RTX A5000 GPU at Ubuntu 20.04.6 LTS. For SST, we set low resolution R_PTS = 0.43 (P_L = 48 and Str_L = 16) for long-range time series and high-resolution R_PTS = 0.5 (P_S = 16 and Str_S = 8) for short range. We set the length of long-range time series L as twice as the length of short-range time series S, i.e., L = 2 ∗ S, to obtain global patterns in longer time series. For the length of short-range time series, we set S = 336 to be consistent with PatchTST (Nie et al. 2023) to inherit the merits of the patching. Following most previous work (Liu et al. 2024b; Nie et al. 2023; Zeng et al. 2023), we fix the forecasting length as F ∈ {96, 192, 336, 720}. For the length of local window w in LWT, we set w = 7 for ETTh1, ETTm1, ETTm2, and Weather, w = 21 for ETTh2, w = 31 for ECL and Traffic due to the hyperpamrater tuning. The experimental setting of baselines either follows the latest SOTA iTransformer (Liu et al. 2024b) (if applicable) or based on configurations of the original paper. For the Mambaformer family in the ablation studies, we set input length as 336 like SST, and report the average value of results across forecasting lengths F ∈ {96, 192, 336, 720}.
Mambaformer in the Ablation Studies

Recent findings show that SSMs and Transformers are complementary for language modeling (Lieber et al. 2024; Fathi et al. 2023; Park et al. 2024). Mambaformer (Park et al. 2024) is early work to combine Mamba and Transformer in text data where Mambaformer attempts to combine the advantages of Mamba and Transformer by directly interleaving Mamba and attention layer. Although Mambaformer has been proved effective for in-context learning tasks of text data, we are interested in if the observation is consistent in time series data given such directly stacking design of Mambaformer. Therefore, we adapt Mambaformer to time series data and compare Mambaformer family with SST in the ablation studies.
Here we introduce the details of Mambaformer. Following (Park et al. 2024), Mambaformer adopts a decoder-only style as GPT (Radford et al. 2018, 2019; Brown et al. 2020) family. As shown in Figure 8, Mambaformer includes an embedding layer to encode token and temporal information, a Mamba pre-processing layer to incorporate positional encoding, a core Mambaformer layer to capture long- and short-range time series dependencies, and a forecasting layer to output forecasts.
Embedding Layer
We utilize an embedding layer to map the low-dimension time series data into a high-dimensional space, including token embedding and temporal embedding.
Token Embedding.
To convert raw time series data into high-dimensional tokens, we utilize a one-dimensional convolutional layer as a token embedding module because it can retain local semantic information within the time series data (Chang, Peng, and Chen 2023).
Temporal Embedding.
Besides numerical value itself in the sequence, temporal context information also provides informative clues, such as hierarchical timestamps (week, month and year) and agnostic timestamps (holidays and events) (Zeng et al. 2023). We employ a linear layer to embed temporal context information.
Formally, let X ∈ R B×L×M denote input sequences with batch size B, input length L, and input variate dimension M. C ∈ R B×L×C denotes the associated temporal context information, e.g. day-of-the-week and hour-of-the-day, with dimension C. The embedding layer can be expressed as follows:
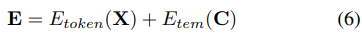
where E ∈ R B×L×D is output embedding, D is the dimension of the embedding, E_token and E_tem denote toke embedding layer and temporal embedding layer, respectively.
We do not need a positional embedding typically existing in Transformer model. Instead, a Mamba pre-processing block introduced in the next subsection is leveraged to internally incorporate positional information to the embedding.
Mamba Pre-Processing Layer
To endow the embedding with positional information, we pre-process the sequence by a Mamba block to internally embed order information of input tokens. Mamba can be regarded as a RNN where the hidden state ht at current time t is updated by the hidden state ht−1 at previous time t − 1 as shown in the Equation 2. Such recurrence mechanism to process tokens enables Mamba naturally consider order information of sequences. Therefore, unlike positional encoding being an essential component in Transformer, Mambaformer replace positional encoding by a Mamba pre-processing block. In a formal way, the Mamba pre-processing block can be expressed as follows:

where H1 ∈ R B×L×D denotes a mixing representation including token embedding, temporal embedding, and positional information.
Mambaformer Layer
The core Mambaformer layer interleaves Mamba layer and self-attention layer to attempt to integrate advantages of Mamba and Transformer to facilitate long-short range time series forecasting.
Attention Layer.
To inherit impressive performance of depicting short-range time series dependencies in the transformer, we leverage masked multi-head attention layer to obtain correlations between tokens. In particular, each head

wards, a scaled dot-product attention is utilized:
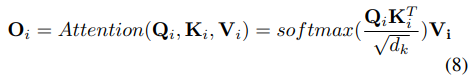
where the outputs Oi of each head are concatenated into a output vector O with the embedding dimension hd_v. Following a learnable projection matrix

, the output of attention layer
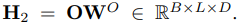
We adopt the masking mechanism to prevent positions from attending to subsequent positions, and set dk = dv = D/h following vanilla Transformer setting (Vaswani et al. 2017).
Mamba Layer.
To overcome computational challenges of the Transformer and be beyond the performance of Transformer, we incorporate the Mamba layer into the model to enhance the capability of capturing long-range time series dependency. As shown in Figure 8, Mamba block is a sequence-sequence module with the same dimension of input and output. In particularly, Mamba takes an input H2 and expand the dimension by two input linear projection. For one projection, Mamba processes the expanded embedding through a convolution and SiLU activation before feeding into the SSM. The core discretized SSM module is able to select input-dependent knowledge and filter out irrelevant information. The other projection followed by SiLU activation, as a residual connection, is combined with the output of the SSM module through a multiplicative gate. Finally, Mamba delivers output H3 ∈ R B×L×D through an output linear projection.
Forecasting Layer
At this layer, we obtain forecasting resulting by a linear layer to convert high-dimension embedding space into original dimension of time series data as follows:

Mambaformer Family in the Ablation Studies
We introduce Mambaformer family by exploring more possible hybrid architectures of Mamba and Transformer. As shown in Figure 9, we interleave Mamba layer and attention layer in different orders and compare them with Mamba and vanilla Transformer. The architectures of Mambaformer family is as follows:
• Mambaformer utilizes a pre-processing Mamba block and Mambaformer layer without a positional encoding.
• Attention-Mamba leverages a Attention-Mamba layer where an attention layer is followed by a Mamba layer with a positional encoding.
• Mamba-Attention adopts a Mamba-Attention layer where a Mamba block layer is followed by an attention layer without a positional encoding.
For convenience of compression, we also depicts Mamba and vanilla Transformer in Figure 9.
• Mamba leverages two Mamba block as a layer.
• Transformer denotes a decoder-only vanilla Transformer architecture.
Positional encoding is optional in the above architectures because Mamba layer internally consider positional information while Transformer does not. For Mambaformer family, if a Mamba layer is before an attention layer, the model does not need a positional encoding; if not, the model needs a positional encoding.

References
Gu, A.; and Dao, T. 2023. Mamba: Linear-time sequence modeling with selective state spaces. arXiv preprint arXiv:2312.00752.
Gu, A.; Dao, T.; Ermon, S.; Rudra, A.; and Re, C. 2020. Hippo: Recurrent memory with optimal polynomial projections. Advances in neural information processing systems, 33: 1474–1487.
Gu, A.; Goel, K.; and Re, C. 2022. Efficiently Modeling Long Sequences with Structured State Spaces. In International Conference on Learning Representations.
Gu, A.; Johnson, I.; Goel, K.; Saab, K.; Dao, T.; Rudra, A.; and Re, C. 2021. Combining recurrent, convolutional, and continuous-time models with linear state space layers. Advances in neural information processing systems, 34: 572– 585.
Dao, T.; and Gu, A. 2024. Transformers are SSMs: Generalized models and efficient algorithms through structured state space duality. arXiv preprint arXiv:2405.21060.
Fedus, W.; Zoph, B.; and Shazeer, N. 2022. Switch transformers: Scaling to trillion parameter models with simple and efficient sparsity. Journal of Machine Learning Research, 23(120): 1–39.
Li, S.; Jin, X.; Xuan, Y.; Zhou, X.; Chen, W.; Wang, Y.-X.; and Yan, X. 2019. Enhancing the locality and breaking the memory bottleneck of transformer on time series forecasting. Advances in neural information processing systems, 32.
Liu, S.; Yu, H.; Liao, C.; Li, J.; Lin, W.; Liu, A. X.; and Dustdar, S. 2021. Pyraformer: Low-complexity pyramidal attention for long-range time series modeling and forecasting. In International conference on learning representations.
Liu, Y.; Hu, T.; Zhang, H.; Wu, H.; Wang, S.; Ma, L.; and Long, M. 2024b. iTransformer: Inverted Transformers Are Effective for Time Series Forecasting. In The Twelfth International Conference on Learning Representations.
Nie, Y.; Nguyen, N. H.; Sinthong, P.; and Kalagnanam, J. 2023. A Time Series is Worth 64 Words: Long-term Forecasting with Transformers. In The Eleventh International Conference on Learning Representations.
Wen, Q.; Zhou, T.; Zhang, C.; Chen, W.; Ma, Z.; Yan, J.; and Sun, L. 2023. Transformers in Time Series: A Survey. In Elkind, E., ed., Proceedings of the Thirty-Second International Joint Conference on Artificial Intelligence, IJCAI-23, 6778–6786. International Joint Conferences on Artificial Intelligence Organization. Survey Track.
Zeng, A.; Chen, M.; Zhang, L.; and Xu, Q. 2023. Are transformers effective for time series forecasting? In Proceedings of the AAAI conference on artificial intelligence, volume 37, 11121–11128.
Wu, H.; Xu, J.; Wang, J.; and Long, M. 2021. Autoformer: Decomposition transformers with auto-correlation for long-term series forecasting. Advances in neural information processing systems, 34: 22419–22430.
Zhang, Y.; and Yan, J. 2022. Crossformer: Transformer utilizing cross-dimension dependency for multivariate time series forecasting. In The eleventh international conference on learning representations.
Zhou, H.; Zhang, S.; Peng, J.; Zhang, S.; Li, J.; Xiong, H.; and Zhang, W. 2021. Informer: Beyond efficient transformer for long sequence time-series forecasting. In Proceedings of the AAAI conference on artificial intelligence, volume 35, 11106–11115.
Zhou, T.; Ma, Z.; Wen, Q.; Wang, X.; Sun, L.; and Jin, R. 2022. Fedformer: Frequency enhanced decomposed transformer for long-term series forecasting. In International Conference on Machine Learning, 27268–27286. PMLR.
Lieber, O.; Lenz, B.; Bata, H.; Cohen, G.; Osin, J.; Dalmedigos, I.; Safahi, E.; Meirom, S.; Belinkov, Y.; ShalevShwartz, S.; Abend, O.; Alon, R.; Asida, T.; Bergman, A.; Glozman, R.; Gokhman, M.; Manevich, A.; Ratner, N.; Rozen, N.; Shwartz, E.; Zusman, M.; and Shoham, Y. 2024. Jamba: A Hybrid Transformer-Mamba Language Model. arXiv:2403.19887.
Patro, B. N.; and Agneeswaran, V. S. 2024. SiMBA: Simplified Mamba-Based Architecture for Vision and Multivariate Time series. arXiv preprint arXiv:2403.15360.
Park, J.; Park, J.; Xiong, Z.; Lee, N.; Cho, J.; Oymak, S.; Lee, K.; and Papailiopoulos, D. 2024. Can Mamba Learn How to Learn? A Comparative Study on In-Context Learning Tasks. arXiv preprint arXiv:2402.04248.
Tang, Y.; Dong, P.; Tang, Z.; Chu, X.; and Liang, J. 2024. VMRNN: Integrating Vision Mamba and LSTM for Efficient and Accurate Spatiotemporal Forecasting. arXiv:2403.16536.
Wang, Z.; Kong, F.; Feng, S.; Wang, M.; Zhao, H.; Wang, D.; and Zhang, Y. 2024b. Is Mamba Effective for Time Series Forecasting? arXiv preprint arXiv:2403.11144.
Ahamed, M. A.; and Cheng, Q. 2024. TimeMachine: A Time Series is Worth 4 Mambas for Long-term Forecasting. arXiv preprint arXiv:2403.09898.
Zhu, L.; Liao, B.; Zhang, Q.; Wang, X.; Liu, W.; and Wang, X. 2024. Vision mamba: Efficient visual representation learning with bidirectional state space model. arXiv preprint arXiv:2401.09417.
Gruver, N.; Finzi, M.; Qiu, S.; and Wilson, A. G. 2024. Large language models are zero-shot time series forecasters. Advances in Neural Information Processing Systems, 36.
Jin, M.; Wang, S.; Ma, L.; Chu, Z.; Zhang, J. Y.; Shi, X.; Chen, P.-Y.; Liang, Y.; Li, Y.-F.; Pan, S.; et al. 2023. Timellm: Time series forecasting by reprogramming large language models. arXiv preprint arXiv:2310.01728.
Tan, M.; Merrill, M. A.; Gupta, V.; Althoff, T.; and Hartvigsen, T. 2024. Are Language Models Actually Useful for Time Series Forecasting? arXiv preprint arXiv:2406.16964.
Wu, H.; Hu, T.; Liu, Y.; Zhou, H.; Wang, J.; and Long, M. 2022. Timesnet: Temporal 2d-variation modeling for general time series analysis. In The eleventh international conference on learning representations.
'NLP > NLP_Paper' 카테고리의 다른 글