-
[SimPO] Simple Preference Optimization with a Reference-Free RewardResearch/..... 2024. 12. 14. 12:11
https://arxiv.org/pdf/2405.14734
https://github.com/princeton-nlp/SimPO
May 2024 (NeurlPS 2024)
Abstract
Direct Preference Optimization (DPO) is a widely used offline preference optimization algorithm that reparameterizes reward functions in reinforcement learning from human feedback (RLHF) to enhance simplicity and training stability. In this work, we propose SimPO, a simpler yet more effective approach. The effectiveness of SimPO is attributed to a key design: using the average log probability of a sequence as the implicit reward. This reward formulation better aligns with model generation and eliminates the need for a reference model, making it more compute and memory efficient. Additionally, we introduce a target reward margin to the Bradley-Terry objective to encourage a larger margin between the winning and losing responses, further improving the algorithm’s performance. We compare SimPO to DPO and its recent variants across various state-of-the-art training setups, including both base and instruction-tuned models such as Mistral, Llama 3, and Gemma 2. We evaluate on extensive chat-based evaluation benchmarks, including AlpacaEval 2, MT-Bench, and Arena-Hard. Our results demonstrate that SimPO consistently and significantly outperforms existing approaches without substantially increasing response length. Specifically, SimPO outperforms DPO by up to 6.4 points on AlpacaEval 2 and by up to 7.5 points on Arena-Hard. Our top-performing model, built on Gemma-2-9B-it, achieves a 72.4% length-controlled win rate on AlpacaEval 2, a 59.1% win rate on Arena-Hard, and ranks 1st on Chatbot Arena among <10B models with real user votes.1
1. Introduction
Learning from human feedback is crucial in aligning large language models (LLMs) with human values and intentions [51], ensuring they are helpful, honest, and harmless [5]. Reinforcement learning from human feedback (RLHF) [18, 62, 73] is a popular method for fine-tuning language models to achieve effective alignment. While the classical RLHF approach [62, 70] has shown impressive results, it presents optimization challenges due to its multi-stage procedure, which involves training a reward model and then optimizing a policy model to maximize that reward [13].
Recently, researchers have been exploring simpler offline algorithms. Direct Preference Optimization (DPO) [66] is one such approach. DPO reparameterizes the reward function in RLHF to directly learn a policy model from preference data, eliminating the need for an explicit reward model. It has gained widespread practical adoption due to its simplicity and stability. In DPO, the implicit reward is formulated using the log ratio of the likelihood of a response between the current policy model and the supervised fine-tuned (SFT) model. However, this reward formulation is not directly aligned with the metric used to guide generation, which is approximately the average log likelihood of a response generated by the policy model. We hypothesize that this discrepancy between training and inference may lead to suboptimal performance.
In this work, we propose SimPO, a simple yet effective offline preference optimization algorithm (Figure 1). The core of our algorithm aligns the reward function in the preference optimization objective with the generation metric. SimPO consists of two major components: (1) a length-normalized reward, calculated as the average log probability of all tokens in a response using the policy model, and (2) a target reward margin to ensure the reward difference between winning and losing responses exceeds this margin. In summary, SimPO has the following properties:
• Simplicity: SimPO does not require a reference model, making it more lightweight and easier to implement compared to DPO and other reference-based methods.
• Significant performance advantage: Despite its simplicity, SimPO significantly outperforms DPO and its latest variants (e.g., a recent reference-free objective ORPO [42]). The performance advantage is consistent across various training setups and extensive chat-based evaluations, including AlpacaEval 2 [55, 28] and the challenging Arena-Hard [54] benchmark. It achieves up to a 6.4 point improvement on AlpacaEval 2 and a 7.5 point improvement on Arena-Hard compared to DPO (Figure 1).
• Minimal length exploitation: SimPO does not significantly increase response length compared to the SFT or DPO models (Table 1), indicating minimal length exploitation [28, 71, 85].
Extensive analysis shows that SimPO utilizes preference data more effectively, leading to a more accurate likelihood ranking of winning and losing responses on a held-out validation set, which in turn translates to a better policy model. As shown in Table 1, our Gemma-2-9B-it-SimPO model achieves state-of-the-art performance, with a 72.4% length-controlled win rate on AlpacaEval 2 and a 59.1% win rate on Arena-Hard, establishing it as the strongest open-source model under 10B parameters. Most notably, when evaluated on Chatbot Arena [17] with real user votes, our model significantly improved upon the initial Gemma-2-9B-it model, advancing from 36th to 25th place and ranking first among all <10B models on the leaderboard.2


2. SimPO: Simple Preference Optimization
In this section, we first introduce the background of DPO (§2.1). Then we identify the discrepancy between DPO’s reward and the likelihood metric used for generation, and propose an alternative reference-free reward formulation that mitigates this issue (§2.2). Finally, we derive the SimPO objective by incorporating a target reward margin term into the Bradley-Terry model (§2.3).
2.1. Background: Direct Preference Optimization (DPO)
DPO [66] is one of the most popular preference optimization methods. Instead of learning an explicit reward model [62], DPO reparameterizes the reward function r using a closed-form expression with the optimal policy:

where πθ is the policy model, πref is the reference policy, typically the supervised fine-tuned (SFT) model, and Z(x) is the partition function. By incorporating this reward formulation into the Bradley-Terry (BT) ranking objective [11], p(yw ≻ yl | x) = σ (r(x, yw) − r(x, yl)), DPO expresses the probability of preference data with the policy model rather than the reward model, yielding the following objective:

where (x, yw, yl) are preference pairs consisting of the prompt, the winning response, and the losing response from the preference dataset D.
2.2. A Simple Reference-Free Reward Aligned with Generation
Discrepancy between reward and generation for DPO.
Using Eq. (1) as the implicit reward has the following drawbacks: (1) it requires a reference model πref during training, which incurs additional memory and computational costs; and (2) it creates a mismatch between the reward optimized in training and the log-likelihood optimized during inference, where no reference model is involved. This means that in DPO, for any triple (x, yw, yl), satisfying the reward ranking r(x, yw) > r(x, yl) does not necessarily mean that the likelihood ranking pθ(yw | x) > pθ(yl | x) is met (here pθ is the average log-likelihood in Eq. (3)). In our experiments, we observed that only ∼ 50% of the triples from the training set satisfy this condition when trained with DPO (Figure 4b). This observation aligns with a concurrent work [14], which finds that existing models trained with DPO exhibit random ranking accuracy in terms of average log-likelihood, even after extensive preference optimization.
Length-normalized reward formulation.
One solution is to use the summed token log probability as the reward, but this suffers from length bias–longer sequences tend to have lower log probabilities. Consequently, when yw is longer than yl , optimizing the summed log probability as a reward forces the model to artificially inflate probabilities for longer sequences to ensure yw receives a higher reward than yl . This overcompensation increases the risk of degeneration. To address this issue, we consider using the average log-likelihood as the implicit reward:

This metric is commonly used for ranking options in beam search [35, 53] and multiple-choice tasks within language models [12, 41, 62]. Naturally, we consider replacing the reward formulation in DPO with pθ in Eq. (3), so that it aligns with the likelihood metric that guides generation. This results in a length-normalized reward:

where β is a constant that controls the scaling of the reward difference. We find that normalizing the reward with response lengths is crucial; removing the length normalization term from the reward formulation results in a bias toward generating longer but lower-quality sequences (see Section 4.4 for more details). Consequently, this reward formulation eliminates the need for a reference model, enhancing memory and computational efficiency compared to reference-dependent algorithms.
2.3. The SimPO Objective
Target reward margin.
Additionally, we introduce a target reward margin term, γ > 0, to the Bradley-Terry objective to ensure that the reward for the winning response, r(x, yw), exceeds the reward for the losing response, r(x, yl), by at least γ:

The margin between two classes is known to influence the generalization capabilities of classifiers [1, 10, 22, 31].3 In standard training settings with random model initialization, increasing the target margin typically improves generalization. In preference optimization, the two classes are the winning and losing responses for a single input. In practice, we observe that generation quality initially improves with an increasing target margin but degrades when the margin becomes too large (§4.3). One of DPO’s variants, IPO [6], also formulates a target reward margin similar to SimPO. However, its full objective is not as effective as SimPO (§4.1).
Objective.
Finally, we obtain the SimPO objective by plugging Eq. (4) into Eq. (5):

In summary, SimPO employs an implicit reward formulation that directly aligns with the generation metric, eliminating the need for a reference model. Additionally, it introduces a target reward margin γ to help separating the winning and losing responses. In Appendix F, we provide a gradient analysis of SimPO and DPO to further understand the differences between the two methods.
Preventing catastrophic forgetting without KL regularization.
Although SimPO does not impose KL regularization, we find that a combination of practical factors ensures effective learning from preference data while maintaining generalization, leading to an empirically low KL divergence from the reference model. These factors are: (1) a small learning rate, (2) a preference dataset that covers diverse domains and tasks, and (3) the intrinsic robustness of LLMs to learn from new data without forgetting prior knowledge. We present KL divergence experiments in Section 4.4.
3. Experimental Setup
Models and training settings.
We perform preference optimization with two families of models, Llama-3-8B [2] and Mistral-7B [44], under two setups: Base and Instruct. In this section, our goal is to understand the performance of SimPO vs. other preference optimization methods in different experimental setups. Our strongest model is based on Gemma-2-9B (Instruct setup) with a stronger reward model, RLHFlow/ArmoRM-Llama3-8B-v0.1 [84] (Table 1). We will present and discuss these results in Appendix J.
For the Base setup, we follow the training pipeline of Zephyr [80]. First, we train a base model (i.e., mistralai/Mistral-7B-v0.1, or meta-llama/Meta-Llama-3-8B) on the UltraChat-200k dataset [25] to obtain an SFT model. Then, we perform preference optimization on the UltraFeedback dataset [23] using the SFT model as the starting point. This setup provides a high level of transparency, as the SFT models are trained on open-source data.
For the Instruct setup, we use an off-the-shelf instruction-tuned model (i.e., meta-llama/MetaLlama-3-8B-Instruct, or mistralai/Mistral-7B-Instruct-v0.2) as the SFT models.4 These models have undergone extensive instruction-tuning processes, making them more powerful and robust than the SFT models in the Base setup. However, they are also more opaque because their RLHF procedure is not publicly disclosed. To mitigate the distribution shift between SFT models and the preference optimization process, we generate the preference dataset using the SFT models following [79]. This makes our Instruct setup closer to an on-policy setting. Specifically, we use prompts from the UltraFeedback dataset and regenerate the chosen and rejected response pairs (yw, yl) with the SFT models. For each prompt x, we generate 5 responses using the SFT model with a sampling temperature of 0.8. We then use llm-blender/PairRM [45] to score the 5 responses, selecting the highest-scoring one as yw and the lowest-scoring one as yl . We only generated data in a single pass instead of iteratively as in [79].5
In summary, we have four setups: Llama-3-Base, Llama-3-Instruct, Mistral-Base, and Mistral-Instruct. We believe these configurations represent the state-of-the-art, placing our models among the top performers on various leaderboards. We encourage future research to adopt these settings for better and fairer comparisons of different algorithms. Additionally, we find that tuning hyperparameters is crucial for achieving optimal performance with all the offline preference optimization algorithms, including DPO and SimPO. Generally, for SimPO, setting β between 2.0 and 2.5 and γ between 0.5 and 1.5 leads to good performance across all setups. For more details, please refer to Appendix B.
Evaluation benchmarks.
We primarily assess our models using three of the most popular open-ended instruction-following benchmarks: MT-Bench [99], AlpacaEval 2 [55], and Arena-Hard v0.1 [54]. These benchmarks evaluate the models’ versatile conversational abilities across a diverse set of queries and have been widely adopted by the community (details in Table 2). AlpacaEval 2 consists of 805 questions from 5 datasets, and MT-Bench covers 8 categories with 80 questions. The most recently released Arena-Hard is an enhanced version of an MT-Bench, incorporating 500 well-defined technical problem-solving queries. We report scores following each benchmark’s evaluation protocol. For AlpacaEval 2, we report both the raw win rate (WR) and the length-controlled win rate (LC) [28]. The LC metric is specifically designed to be robust against model verbosity. For Arena-Hard, we report the win rate (WR) against the baseline model. For MT-Bench, we report the average MT-Bench score with GPT-4 and GPT-4-Preview-1106 as the judge model.6 For decoding details, please refer to Appendix B. We also evaluate on downstream tasks from the Huggingface Open Leaderboard benchmarks [9], with additional details in in Appendix C.

Baselines.
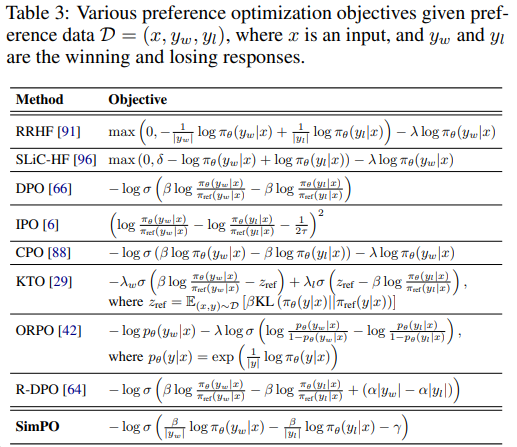
We compare SimPO with other offline preference optimization methods listed in Table 3. 7 RRHF [91] and SLiC-HF [96] are ranking losses. RRHF uses length-normalized log-likelihood, similar to SimPO’s reward function, while SLiCHF uses log-likelihood directly and includes an SFT objective. IPO [6] is a theoretically grounded approach method that avoids DPO’s assumption that pairwise preferences can be replaced with pointwise rewards. CPO [88] uses sequence likelihood as a reward and trains alongside an SFT objective. KTO [29] learns from non-paired preference data. ORPO [42] 8 introduces a reference-model-free odd ratio term to directly contrast winning and losing responses with the policy model and jointly trains with the SFT objective. R-DPO [64] is a modified version of DPO that includes an additional regularization term to prevent exploitation of length. We thoroughly tune the hyperparameters for each baseline and report the best performance. We find that many variants of DPO do not empirically present an advantage over standard DPO. Further details can be found in Appendix B.


4. Experimental Results
In this section, we present main results of our experiments, highlighting the superior performance of SimPO on various benchmarks and ablation studies (§4.1). We provide an in-depth understanding of the following components: (1) length normalization (§4.2), (2) the margin term γ (§4.3), and (3) why SimPO outperforms DPO (§4.4). Unless otherwise specified, the ablation studies are conducted using the Mistral-Base setting.
4.1. Main Results and Ablations
SimPO consistently and significantly outperforms existing preference optimization methods.
As shown in Table 4, while all preference optimization algorithms enhance performance over the SFT model, SimPO, despite its simplicity, achieves the best overall performance across all benchmarks and settings. These consistent and significant improvements highlight the robustness and effectiveness of SimPO. Notably, SimPO outperforms the best baseline by 3.6 to 4.8 points on the AlpacaEval 2 LC win rate across various settings. On Arena-Hard, SimPO consistently achieves superior performance, though it is occasionally surpassed by CPO [88]. We find that CPO generates responses that are, on average, 50% longer than those generated by SimPO (See Table 10). Arena-Hard might favor longer generations due to the absence of a length penalty in its evaluation.

Benchmark quality varies.
Although all three benchmarks are widely adopted, we find that MTBench exhibits poor separability across different methods. Minor differences between methods on MT-Bench may be attributed to randomness, likely due to the limited scale of its evaluation data and its single-instance scoring protocol. This finding aligns with observations reported in [54]. In contrast, AlpacaEval 2 and Arena-Hard provide more meaningful distinctions between different methods. We observe that the win rate on Arena-Hard is significantly lower than on AlpacaEval 2, indicating that Arena-Hard is a more challenging benchmark.9

The Instruct setting introduces significant performance gains.
Across all benchmarks, we observe that the Instruct setting consistently outperforms the Base setting. This improvement is likely due to the higher quality of SFT models used for initialization and the generation of more high-quality preference data by these models.
Both key designs in SimPO are crucial.
In Table 5, we demonstrate results from ablating each key design of SimPO: (1) removing length normalization in Eq. (4) (i.e., w/o LN); (2) setting the target reward margin to be 0 in Eq. (6) (i.e., γ = 0). Removing the length normalization has the most negative impact on the results. Our examination reveals that this leads to the generation of long and repetitive patterns, substantially degrading the overall quality of the output (See Appendix E). Setting γ to 0 yields also leads to a performance degradation compared to SimPO, indicating that it is not the optimal target reward margin. In the following subsections, we conduct in-depth analyses to better understand both design choices.

4.2. Length Normalization (LN) Prevents Length Exploitation
LN leads to an increase in the reward difference for all preference pairs, regardless of their length.
The Bradley-erry objective in Eq. (5) essentially aims to optimize the reward difference ∆r = r(x, yw) − r(x, yl) to exceed the target margin γ. We investigate the relationship between the learned reward differences and the length difference ∆l = |yw| − |yl | between the winning and losing responses from the training set of UltraFeedback. We measure the difference of reward (rSimPO; Eq. (4)) using the SFT model, the SimPO model, and a model trained with SimPO but without length normalization. We present the results in Figure 2a and observe that SimPO with LN consistently achieves a positive reward margin for all response pairs, regardless of their length difference, and consistently improves the margin over the SFT model. In contrast, SimPO without LN results in a negative reward difference for preference pairs when the winning response is shorter than the losing response, indicating that the model learns poorly for these instances.
Removing LN results in a strong positive correlation between the reward and response length, leading to length exploitation.
Figures 2b and 2c illustrate the average log likelihood (pθ in Eq. (3)) versus response length on a held-out set for models trained with SimPO and SimPO without LN. The model trained without LN exhibits a much stronger positive Spearman correlation between likelihood and response length compared to SimPO, indicating a tendency to exploit length bias and generate longer sequences (see Appendix E). In contrast, SimPO results in a Spearman correlation coefficient similar to the SFT model (see Figure 6a).
4.3. The Impact of Target Reward Margin in SimPO
Influence of γ on reward accuracy and win rate.
We investigate how the target reward margin γ in SimPO affects the reward accuracy on a held-out set and win rate on AlpacaEval 2, presenting the results in Figure 3a. Reward accuracy is measured as the percentage of preference pairs where the winning response ends up having a higher reward for the winning response than the losing response (i.e., r(x, yw) > r(x, yl)). We observe that reward accuracy increases with γ on both benchmarks, indicating that enforcing a larger target reward margin effectively improves reward accuracy. However, the win rate on AlpacaEval 2 first increases and then decreases with γ, suggesting that generation quality is not solely determined by the reward margin.

Impact of γ on the reward distribution.
We visualize the distribution of the learned reward margin r(x, yw)−r(x, yl) and the reward of winning responses r(x, yw) under varying γ values in Figure 2b and Figure 2c. Notably, increasing γ tends to flatten both distributions and reduce the average log likelihood of winning sequences. This initially improves performance but can eventually lead to model degeneration. We hypothesize that there is a trade-off between accurately approximating the true reward distribution and maintaining a well-calibrated likelihood when setting the γ value. Further exploration of this balance is deferred to future work.
4.4. In-Depth Analysis of DPO vs. SimPO
In this section, we compare SimPO to DPO in terms of (1) likelihood-length correlation, (2) reward formulation, (3) reward accuracy, and (4) algorithm efficiency. We demonstrate that SimPO outperforms DPO in terms of reward accuracy and efficiency.
DPO reward implicitly facilitates length normalization.
Although the DPO reward expression r(x, y) = β log πθ(y|x) / πref(y|x) (with the partition function excluded) lacks an explicit term for length normalization, the logarithmic ratio between the policy model and the reference model can serve to implicitly counteract length bias. As shown in Table 6 and Figure 4a, employing DPO reduces the Spearman correlation coefficient between average log likelihood and response length compared to the approach without any length normalization (referred to as “SimPO w/o LN”). However, it still exhibits a stronger positive correlation when compared to SimPO.10


DPO reward mismatches generation likelihood.
There is a divergence between DPO’s reward formulation, rθ(x, y) = β log πθ(y|x) / πref(y|x) , and the average log likelihood metric, pθ(y | x) = 1 / |y| * log πθ(y | x), which directly impacts generation. As shown in Figure 4b, among the instances on the UltraFeedback training set where rθ(x, yw) > rθ(x, yl) , almost half of the pairs have pθ(yw | x) < pθ(yl | x). In contrast, SimPO directly employs the average log likelihood (scaled by β) as the reward expression, thereby eliminating the discrepancy completely, as demonstrated in Figure 6b.
DPO lags behind SimPO in terms of reward accuracy.
In Figure 4c, we compare the reward accuracy of SimPO and DPO, assessing how well their final learned rewards align with preference labels on a held-out set. SimPO consistently achieves higher reward accuracy than DPO, suggesting that our reward design facilitates better generalization and leads to higher quality generations.
KL divergence of SimPO and DPO.
In Figure 5a, we present the KL divergence between the policy model trained with DPO and SimPO and the reference model with different β, measured on the winning responses from a held-out set during training. Figure 5b shows the corresponding AlpacaEval 2 LC win rate. Although SimPO does not apply any form of regularization against the reference model, the KL divergence of SimPO is reasonably small. Increasing β reduces the KL divergence for both DPO and SimPO, with DPO exhibiting a more pronounced reduction at higher β values. In this particular setting (Mistral-base), Figure 5b demonstrates that a smaller β can improve AlpacaEval 2 performance, despite the higher KL divergence.11 We hypothesize that when the reference model is weak, strictly constraining the policy model to the reference model may not be beneficial. As a caveat, while we did not observe any training collapse or degeneration with proper tuning, in principle, SimPO could potentially lead to reward hacking without explicit regularization against the reference model. In such a scenario, the model might achieve a low loss but degenerate.
SimPO is more memory and compute-efficient than DPO.
Another benefit of SimPO is its efficiency as it does not use a reference model. Figure 5c illustrates the overall run time and per-GPU peak memory usage of SimPO and DPO in the Llama-3-Base setting using 8×H100 GPUs. Compared to a vanilla DPO implementation,12 SimPO cuts run time by roughly 20% and reduces GPU memory usage by about 10%, thanks to eliminating forward passes with the reference model.
5. Related Work
Reinforcement learning from human feedback.
RLHF is a technique that aligns large language models with human preferences and values [18, 102, 62, 7]. The classical RLHF pipeline typically comprises three phases: supervised fine-tuning [101, 76, 33, 21, 48, 25, 82, 15, 86], reward model training [32, 60, 16, 56, 37, 50], and policy optimization [70, 4]. Proximal Policy Optimization (PPO) [70] is a widely used algorithm in the third stage of RLHF. The RLHF framework is also widely applied to various applications, such as mitigating toxicity [3, 49, 97], ensuring safety [24], enhancing helpfulness [78, 83], searching and navigating the web [61], and improving model reasoning abilities [36]. Recently, [13] has highlighted challenges across the whole RLHF pipeline from preference data collection to model training. Further research has also demonstrated that RLHF can lead to biased outcomes, such as verbose outputs from the model [28, 71, 85].
Offline vs. iterative preference optimization.
Given that online preference optimization algorithms are complex and difficult to optimize [100, 69], researchers have been exploring more efficient and simpler alternative offline algorithms. Direct Preference Optimization (DPO) [66] is a notable example. However, the absence of an explicit reward model in DPO limits its ability to sample preference pairs from the optimal policy. To address this, researchers have explored augmenting preference data using a trained SFT policy [96] or a refined SFT policy with rejection sampling [59], enabling the policy to learn from data generated by the optimal policy. Further studies have extended this approach to an iterative training setup, by continuously updating the reference model with the most recent policy model or generating new preference pairs at each iteration [27, 46, 67, 87, 92]. In this work, we focus exclusively on offline settings, avoiding any iterative training processes.
Preference optimization objectives.
A variety of preference optimization objectives have been proposed besides DPO. Ranking objectives allow for comparisons among more than two instances [26, 58, 72, 91]. Another line of work explores simpler preference optimization objectives that do not rely on a reference model [42, 89], similar to SimPO. [8] proposes a method to jointly optimize instructions and responses, finding it effectively improves DPO. [98] focuses on post-training extrapolation between the SFT and the aligned model to further enhance model performance. In this work, we compare SimPO to a series of offline algorithms, including RRHF [91], SLiC-HF [96], DPO [66], IPO [6], CPO [88], KTO [29], ORPO [42], and R-DPO [64], and find that SimPO can outperform them in both efficiency and performance. Recently, [75] proposed a generalized preference optimization framework unifying different offline algorithms, and SimPO can be seen as a special case.
6. Conclusion
In this work, we propose SimPO, a simple and effective preference optimization algorithm that consistently outperforms existing approaches across various training setups. By aligning the reward function with the generation likelihood and introducing a target reward margin, SimPO eliminates the need for a reference model and achieves strong performance without exploiting the length bias. Extensive analysis demonstrates that the key designs in SimPO are crucial and validates the efficiency and effectiveness of SimPO. A detailed discussion of the limitations can be found in Appendix A.
F. Gradient Analysis
We examine the gradients of SimPO and DPO to understand their different impact on the training process.

represent the gradient weight in SimPO and DPO, respectively. It can be seen that the differences are twofold: (1) comparing the gradient weights sθ and dθ, SimPO’s gradient weight sθ does not involve the reference model and has a straightforward interpretation: the weights will be higher for samples where the policy model incorrectly assigns higher likelihood to yl than yw; (2) comparing the gradient updates, SimPO’s gradients on yl and yw are length-normalized, while DPO’s are not. This corresponds to the empirical findings [64] that DPO may exploit length bias: longer sequences with more tokens will receive larger gradient updates in DPO, dominating the training process.
'Research > .....' 카테고리의 다른 글