[PPO] Proximal Policy Optimization Algorithms

https://arxiv.org/pdf/1707.06347

(Aug 2017)

---

Abstract

We propose a new family of policy gradient methods for reinforcement learning, which alternate between sampling data through interaction with the environment, and optimizing a “surrogate” objective function using stochastic gradient ascent. Whereas standard policy gradient methods perform one gradient update per data sample, we propose a novel objective function that enables multiple epochs of minibatch updates. The new methods, which we call proximal policy optimization (PPO), have some of the benefits of trust region policy optimization (TRPO), but they are much simpler to implement, more general, and have better sample complexity (empirically). Our experiments test PPO on a collection of benchmark tasks, including simulated robotic locomotion and Atari game playing, and we show that PPO outperforms other online policy gradient methods, and overall strikes a favorable balance between sample complexity, simplicity, and wall-time.

---

1. Introduction

In recent years, several different approaches have been proposed for reinforcement learning with neural network function approximators. The leading contenders are deep Q-learning [Mni+15], “vanilla” policy gradient methods [Mni+16], and trust region / natural policy gradient methods [Sch+15b]. However, there is room for improvement in developing a method that is scalable (to large models and parallel implementations), data efficient, and robust (i.e., successful on a variety of problems without hyperparameter tuning). Q-learning (with function approximation) fails on many simple problems1 and is poorly understood, vanilla policy gradient methods have poor data effiency and robustness; and trust region policy optimization (TRPO) is relatively complicated, and is not compatible with architectures that include noise (such as dropout) or parameter sharing (between the policy and value function, or with auxiliary tasks).

 

This paper seeks to improve the current state of affairs by introducing an algorithm that attains the data efficiency and reliable performance of TRPO, while using only first-order optimization. We propose a novel objective with clipped probability ratios, which forms a pessimistic estimate (i.e., lower bound) of the performance of the policy. To optimize policies, we alternate between sampling data from the policy and performing several epochs of optimization on the sampled data.

 

Our experiments compare the performance of various different versions of the surrogate objective, and find that the version with the clipped probability ratios performs best. We also compare PPO to several previous algorithms from the literature. On continuous control tasks, it performs better than the algorithms we compare against. On Atari, it performs significantly better (in terms of sample complexity) than A2C and similarly to ACER though it is much simpler.

---

2. Background: Policy Optimization

2.1. Policy Gradient Methods

Policy gradient methods work by computing an estimator of the policy gradient and plugging it into a stochastic gradient ascent algorithm. The most commonly used gradient estimator has the form

 

where πθ is a stochastic policy and Aˆ t is an estimator of the advantage function at timestep t. Here, the expectation Eˆ t [. . .] indicates the empirical average over a finite batch of samples, in an algorithm that alternates between sampling and optimization. Implementations that use automatic differentiation software work by constructing an objective function whose gradient is the policy gradient estimator; the estimator ˆg is obtained by differentiating the objective

 

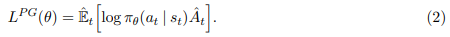
While it is appealing to perform multiple steps of optimization on this loss L^PG using the same trajectory, doing so is not well-justified, and empirically it often leads to destructively large policy updates (see Section 6.1; results are not shown but were similar or worse than the “no clipping or penalty” setting).

---

2.2. Trust Region Methods

In TRPO [Sch+15b], an objective function (the “surrogate” objective) is maximized subject to a constraint on the size of the policy update. Specifically,

 

Here, θold is the vector of policy parameters before the update. This problem can efficiently be approximately solved using the conjugate gradient algorithm, after making a linear approximation to the objective and a quadratic approximation to the constraint.

 

The theory justifying TRPO actually suggests using a penalty instead of a constraint, i.e., solving the unconstrained optimization problem

 

for some coefficient β. This follows from the fact that a certain surrogate objective (which computes the max KL over states instead of the mean) forms a lower bound (i.e., a pessimistic bound) on the performance of the policy π. TRPO uses a hard constraint rather than a penalty because it is hard to choose a single value of β that performs well across different problems—or even within a single problem, where the characteristics change over the course of learning. Hence, to achieve our goal of a first-order algorithm that emulates the monotonic improvement of TRPO, experiments show that it is not sufficient to simply choose a fixed penalty coefficient β and optimize the penalized objective Equation (5) with SGD; additional modifications are required.

---

3. Clipped Surrogate Objective

---

4. Adaptive KL Penalty Coefficient

Another approach, which can be used as an alternative to the clipped surrogate objective, or in addition to it, is to use a penalty on KL divergence, and to adapt the penalty coefficient so that we achieve some target value of the KL divergence dtarg each policy update. In our experiments, we found that the KL penalty performed worse than the clipped surrogate objective, however, we’ve included it here because it’s an important baseline.

 

In the simplest instantiation of this algorithm, we perform the following steps in each policy update:

 

• Using several epochs of minibatch SGD, optimize the KL-penalized objective

 

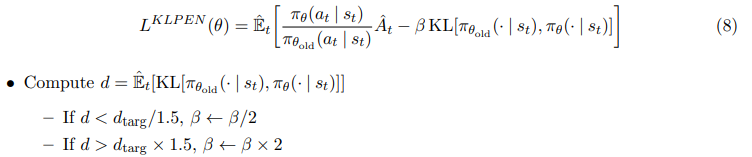
The updated β is used for the next policy update. With this scheme, we occasionally see policy updates where the KL divergence is significantly different from dtarg, however, these are rare, and β quickly adjusts. The parameters 1.5 and 2 above are chosen heuristically, but the algorithm is not very sensitive to them. The initial value of β is a another hyperparameter but is not important in practice because the algorithm quickly adjusts it.

---

5. Algorithm

The surrogate losses from the previous sections can be computed and differentiated with a minor change to a typical policy gradient implementation. For implementations that use automatic differentation, one simply constructs the loss L^CLIP or L^KLPEN instead of L^PG, and one performs multiple steps of stochastic gradient ascent on this objective.

 

Most techniques for computing variance-reduced advantage-function estimators make use a learned state-value function V (s); for example, generalized advantage estimation [Sch+15a], or the finite-horizon estimators in [Mni+16]. If using a neural network architecture that shares parameters between the policy and value function, we must use a loss function that combines the policy surrogate and a value function error term. This objective can further be augmented by adding an entropy bonus to ensure sufficient exploration, as suggested in past work [Wil92; Mni+16]. Combining these terms, we obtain the following objective, which is (approximately) maximized each iteration:

---