Efficient Neural Causal Discovery without Acyclicity Constraints

https://arxiv.org/pdf/2107.10483

https://github.com/phlippe/ENCO

ICLR 2022

 

https://www.youtube.com/watch?v=ro_5FqiS5qU

---

Abstract

Learning the structure of a causal graphical model using both observational and interventional data is a fundamental problem in many scientific fields. A promising direction is continuous optimization for score-based methods, which, however, require constrained optimization to enforce acyclicity or lack convergence guarantees. In this paper, we present ENCO, an efficient structure learning method for directed, acyclic causal graphs leveraging observational and interventional data. ENCO formulates the graph search as an optimization of independent edge likelihoods, with the edge orientation being modeled as a separate parameter. Consequently, we provide for ENCO convergence guarantees when interventions on all variables are available, without having to constrain the score function with respect to acyclicity. In experiments, we show that ENCO can efficiently recover graphs with hundreds of nodes, an order of magnitude larger than what was previously possible, while handling deterministic variables and discovering latent confounders.

---

1. Introduction

Uncovering and understanding causal mechanisms is an important problem not only in machine learning (Schölkopf et al., 2021; Pearl, 2009) but also in various scientific disciplines such as computational biology (Friedman et al., 2000; Sachs et al., 2005), epidemiology (Robins et al., 2000; Vandenbroucke et al., 2016), and economics (Pearl, 2009; Hicks et al., 1980). A common task of interest is causal structure learning (Pearl, 2009; Peters et al., 2017), which aims at learning a directed acyclic graph (DAG) in which edges represent causal relations between variables. While observational data alone is in general not sufficient to identify the DAG (Yang et al., 2018; Hauser & Bühlmann, 2012), interventional data can improve identifiability up to finding the exact graph (Eberhardt et al., 2005; Eberhardt, 2008). Unfortunately, the solution space of DAGs grows super-exponentially with the variable count, requiring efficient methods for large graphs. Current methods are typically applied to a few dozens of variables and cannot scale so well, which is imperative for modern applications like learning causal relations with gene editing interventions (Dixit et al., 2016; Macosko et al., 2015).

 

A promising new direction for scaling up DAG discovery methods are continuous-optimization methods (Zheng et al., 2018; 2020; Zhu et al., 2020; Ke et al., 2019; Brouillard et al., 2020; Yu et al., 2019). In contrast to score-based and constrained-based (Peters et al., 2017; Guo et al., 2020) methods, continuous-optimization methods reinterpret the search over discrete graph topologies as a continuous problem with neural networks as function approximators, for which efficient solvers are amenable. To restrict the search space to acyclic graphs, Zheng et al. (2018) first proposed to view the search as a constrained optimization problem using an augmented Lagrangian procedure to solve it. While several improvements have been explored (Zheng et al., 2020; Brouillard et al., 2020; Yu et al., 2019; Lachapelle et al., 2020), constrained optimization methods remain slow and hard to train. Alternatively, it is possible to apply a regularizer (Zhu et al., 2020; Ke et al., 2019) to penalize cyclic graphs. While simpler to optimize, methods relying on acyclicity regularizers commonly lack guarantees for finding the correct causal graph, often converging to suboptimal solutions. Despite the advances, beyond linear, continuous settings (Ng et al., 2020; Varando, 2020) continuous optimization methods still cannot scale to more than 100 variables, often due to difficulties in enforcing acyclicity.

 

In this work, we address both problems. By modeling the orientation of an edge as a separate parameter, we can define the score function without any acyclicity constraints or regularizers. This allows for unbiased low-variance gradient estimators that scale learning to much larger graphs. Yet, if we are able to intervene on all variables, the proposed optimization is guaranteed to converge to the correct, acyclic graph. Importantly, since such interventions might not always be available, we show that our algorithm performs robustly even when intervening on fewer variables and having small sample sizes. We call our method ENCO for Efficient Neural Causal Discovery.

 

We make the following four contributions. Firstly, we propose ENCO, a causal structure learning method for observational and interventional data using continuous optimization. Different from recent methods, ENCO models the edge orientation as a separate parameter. Secondly, we derive unbiased, low-variance gradient estimators, which is crucial for scaling up the model to large numbers of variables. Thirdly, we show that ENCO is guaranteed to converge to the correct causal graph if interventions on all variables are available, despite not having any acyclicity constraints. Yet, we show in practice that the algorithm works on partial intervention sets as well. Fourthly, we extend ENCO to detecting latent confounders. In various experimental settings, ENCO recovers graphs accurately, making less than one error on graphs with 1,000 variables in less than nine hours of computation.

---

2. Background and Related Work

2.1. Causal Graphical Models

---

2.2. Causal Structure Learning

Discovering the graph G from samples of a joint distribution P is called causal structure learning or causal discovery, a fundamental problem in causality (Pearl, 2009; Peters et al., 2017). While often performed from observational data, i.e. samples from P (see Glymour et al. (2019) for an overview), we focus in this paper on algorithms that recover graphs from joint observational and interventional data. Commonly, such methods are grouped into constraint-based and score-based approaches.

Constraint-based methods

use conditional independence tests to identify causal relations (Monti et al., 2019; Spirtes et al., 2000; Kocaoglu et al., 2019; Jaber et al., 2020; Sun et al., 2007; Hyttinen et al., 2014). For instance, the Invariant Causal Prediction (ICP) algorithm (Peters et al., 2016; Christina et al., 2018) exploits that causal mechanisms remain unchanged under an intervention except the one intervened on (Pearl, 2009; Schölkopf et al., 2012). We rely on a similar idea by testing for mechanisms that generalize from the observational to the interventional setting. Another line of work is to extend methods working on observations only to interventions by incorporating those as additional constraints in the structure learning process (Mooij et al., 2020; Jaber et al., 2020).

Score-based methods

on the other hand, search through the space of all possible causal structures with the goal of optimizing a specified metric (Tsamardinos et al., 2006; Ke et al., 2019; Goudet et al., 2017; Zhu et al., 2020). This metric, also referred to as score function, is usually a combination of how well the structure fits the data, for instance in terms of log-likelihood, as well as regularizers for encouraging sparsity. Since the search space of DAGs is super-exponential in the number of nodes, many methods rely on a greedy search, yet returning graphs in the true equivalence class (Meek, 1997; Hauser & Bühlmann, 2012; Wang et al., 2017; Yang et al., 2018). For instance, GIES (Hauser & Bühlmann, 2012) repeatedly adds, removes, and flips the directions of edges in a proposal graph until no higher-scoring graph can be found. The Interventional Greedy SP (IGSP) algorithm (Wang et al., 2017) is a hybrid method using conditional independence tests in its score function.

Continuous-optimization methods

are score-based methods that avoid the combinatorial greedy search over DAGs by using gradient-based methods (Zheng et al., 2018; Ke et al., 2019; Lachapelle et al., 2020; Yu et al., 2019; Zheng et al., 2020; Zhu et al., 2020; Brouillard et al., 2020). Thereby, the adjacency matrix is parameterized by weights that represent linear factors or probabilities of having an edge between a pair of nodes. The main challenge of such methods is how to limit the search space to acyclic graphs. One common approach is to view the search as a constrained optimization problem and deploy an augmented Lagrangian procedure to solve it (Zheng et al., 2018; 2020; Yu et al., 2019; Brouillard et al., 2020), including NOTEARS (Zheng et al., 2018) and DCDI (Brouillard et al., 2020). Alternatively, Ke et al. (2019) propose to use a regularization term penalizing cyclic graphs while allowing unconstrained optimization. However, the regularizer must be designed and weighted such that the correct, acyclic causal graph is the global optimum of the score function.

---

3. Efficient Neural Causal Discovery

3.1. Scope and Assumptions

We consider the task of finding a directed acyclic graph G = (V, E) with N variables of an unknown CGM given observational and interventional samples. Firstly, we assume that: (1) The CGM is causally sufficient, i.e., all common causes of variables are included and observable; (2) We have N interventional datasets, each sparsely intervening on a different variable; (3) The interventions are “perfect” and “stochastic”, meaning the intervention does not set the variable necessarily to a single value. Thereby, we do not strictly require faithfulness, thus also recovering some graphs violating faithfulness. We emphasize that we place no constraints on the domains of the variables (they can be discrete, continuous, or mixed) or the distributions of the interventions. We discuss later how to extend the algorithm to infer causal mechanisms in graphs with latent confounding causal variables. Further, we discuss how to extend the algorithm to support interventions to subsets of variables only.

---

3.2. Overview

ENCO learns a causal graph from observational and interventional data by modelling a probability for every possible directed edge between pairs of variables. The goal is that the probabilities corresponding to the edges of the ground truth graph converge to one, while the probabilities of all other edges converge to zero. For this to happen, we exploit the idea of independent causal mechanisms (Pearl, 2009; Peters et al., 2016), according to which the conditional distributions for all variables in the ground-truth CGM stay invariant under an intervention, except for the intervened ones. By contrast, for graphs modelling the same joint distribution but with a flipped or additional edge, this does not hold (Peters et al., 2016). In short, we search for the graph which generalizes best from observational to interventional data. To implement the optimization, we alternate between two learning stages, that is distribution fitting and graph fitting, visually summarized in Figure 1.

---

---

3.3. Low-Variance Gradient Estimators for Edge Parameters

---

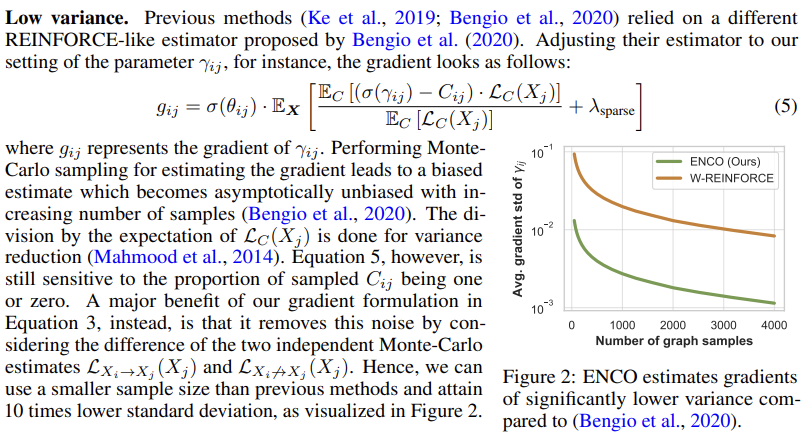
3.4. Convergence Guarantees

Next, we discuss the conditions under which ENCO convergences to the correct causal graph. We show that not only does the global optimum of Equation 2 correspond to the true graph, but also that there exist no other local minima ENCO can converge to. We outline the derivation and proof of these conditions in Appendix B, and limit our discussion here to the main assumptions and implications.

 

To construct a theoretical argument, we make the following assumptions. First, we assume that sparse interventions have been performed on all variables. Later, we show how to extend the algorithm to avoid this strong assumption. Further, given a CGM, we assume that its joint distribution p(X) is Markovian with respect to the true graph G. In other words, the parent set pa(Xi) reflects the inputs to the causal generation mechanism of Xi . We assume that there exist no latent confounders in G. Also, we assume the neural networks in ENCO are sufficiently large and sufficient observational data is provided to model the conditional distributions of the CGM up to an arbitrary small error.

 

Under these assumptions, we produce the following conditions for convergence:

 

Condition 1 and 2 ensure that the orientations can be learned from interventions. Intuitively, ancestors and descendants in the graph have to be dependent when intervening on the ancestors. This aligns with the technical interpretation in Theorem 3.1 that the likelihood estimate of the child variable must improve when intervening and conditioning on its ancestor variables. Condition 3 states intuitively that the sparsity regularizer needs to be selected such that it chooses the sparsest graph among those graphs with equal joint distributions as the ground truth graph, without trading sparsity for worse distribution estimates. The specific condition in Theorem 3.1 ensures thereby that the set can be learned with a gradient-based algorithm. We emphasize that this condition only gives an upper bound for λ_sparse when sufficiently large datasets are available. In practice, the graph can thus be recovered with a sufficiently small sparsity regularizer and dependencies among variables under interventions. We provide more details for various settings and further intuition in Appendix B.

Interventions of fewer variables.

It is straightforward to extend ENCO to support interventions on fewer variables. Normally, in the graph fitting stage, we sample one intervention at a time. We can, thus, simply restrict the sampling only to the interventions that are possible (or provided in the dataset). In this case, we update the orientation parameters θij of only those edges that connect to an intervened variable, either Xi or Xj , as before. For all other orientation parameters, we extend the gradient estimator to include interventions on all variables. Although this estimate is more noisy and does not have convergence guarantees, it can still be informative about the edge orientations.

Enforcing acyclicity

When the conditions are violated, e.g. by limited data, cycles can occur in the prediction. Since ENCO learns the orientations as a separate parameter, we can remove cycles by finding the global order of variables O ∈ S_N , with S_N being the set of permutations, that maximizes the pairwise orientation probabilities: arg max_O summation i=1 N summation j=i+1 N σ(θ_Oi,Oj ). This utilizes the learned ancestor-descendant relations, making the algorithm more robust to noise in single interventions.

---

3.5. Handling Latent Confounders

---

4. Experiments

We evaluate ENCO on structure learning on synthetic datasets for systematic comparisons and real-world datasets for benchmarking against other methods in the literature. The experiments focus on graphs with categorical variables, and experiments on continuous data are included in Appendix D.5. Our code is publicly available at https://github.com/phlippe/ENCO.

---

4.1. Experimental Setup

Graphs and datasets

Given a ground-truth causal graphical model, all methods are tasked to recover the original DAG from a set of observational and interventional data points for each variable. In case of synthetic graphs, we follow the setup of Ke et al. (2019) and create the conditional distributions from neural networks. These networks take as input the categorical values of its variable’s parents, and are initialized orthogonally to output a non-trivial distribution.

Baselines

We compare ENCO to GIES (Hauser & Bühlmann, 2012) and IGSP (Wang et al., 2017; Yang et al., 2018) as greedy score-based approaches, and DCDI (Brouillard et al., 2020) and SDI (Ke et al., 2019) as continuous optimization methods. Further, as a common observational baseline, we apply GES (Chickering, 2002) on the observational data to obtain a graph skeleton, and orient each edge by learning the skeleton on the corresponding interventional distribution. We perform a separate hyperparameter search for all baselines, and use the same neural network setup for SDI, DCDI, and ENCO. Appendix C provides a detailed overview of the hyperparameters for all experiments.

---

4.2. Causal Structure Learning on Common Graph Structures

We first experiment on synthetic graphs. We pick six common graph structures and sample 5,000 observational data points and 200 per intervention. The graphs chain and full represent the minimally- and maximally-connected DAGs. The graph bidiag is a chain with 2-hop connections, and jungle is a tree-like graph. In the collider graph, one node has all other nodes as parents. Finally, random has a randomly sampled graph structure with a likelihood of 0.3 of two nodes being connected by a direct edge. For each graph structure, we generate 25 graphs with 25 nodes each, on which we report the average performance and standard deviation. Following common practice, we use structural hamming distance (SHD) as evaluation metric. SHD counts the number of edges that need to be removed, added, or flipped in order to obtain the ground truth graph.

 

Table 1 shows that the continuous optimization methods outperform the greedy search approaches on categorical variables. SDI works reasonably well on sparse graphs, but struggles with nodes that have many parents. DCDI can recover the collider and full graph to a better degree, yet degrades for sparse graphs. ENCO performs well on all graph structures, outperforming all baselines. For sparse graphs, cycles can occur due to limited sample size. However, with enforcing acyclicity, ENCO-acyclic is able to recover four out of six graphs with less than one error on average. We further include experiments with various sample sizes in Appendix D.1. While other methods do not reliably recover the causal graph even for large sample sizes, ENCO attains low errors even with smaller sample sizes.

---

4.3. Scalability

Next, we test ENCO on graphs with large sets of variables. We create random graphs ranging from N = 100 to N = 1,000 nodes with larger sample sizes. Every node has on average 8 edges and a maximum of 10 parents. The challenge of large graphs is that the number of possible edges grows quadratically and the number of DAGs super-exponentially, requiring efficient methods.

 

We compare ENCO to the two best performing baselines from Table 1, SDI and DCDI. All methods were given the same setup of neural networks and a maximum runtime which corresponds to 30 epochs for ENCO. We plot the SHD over graph size and runtime in Figure 3. ENCO recovers the causal graphs perfectly with no errors except for the 1,000-node graph, for which it misses only one out of 1 million edges in 2 out of 10 experiments. SDI and DCDI achieve considerably worse performance. This shows that ENCO can efficiently be applied to 1,000 variables while maintaining its convergence guarantees, underlining the benefit of its low-variance gradient estimators.

---

4.4. Interventions on Fewer Variables

We perform experiments on the same datasets as in Section 4.2, but provide interventional data only for a randomly sampled subset of the 25 variables of each graph. We compare ENCO to DCDI, which supports partial intervention sets, and plot the SHD over the number of intervened variables in Figure 4. Despite ENCO’s guarantees only holding for full interventions, it is still competitive and outperforms DCDI in most settings. Importantly, enforcing acyclicity has an even greater impact on fewer interventions as more orientations are trained on non-adjacent interventions (see Appendix B.4 for detailed discussion). We conclude that ENCO works competitively with partial interventions too.

---

4.5. Detecting Latent Confounders

To test the detection of latent confounders, we create a set of 25 random graphs with 5 additional latent confounders. The dataset is generated in the same way as before, except that we remove the latent variable from the input data and increase the observational and interventional sample size (see Appendix C.3 for ablation studies). After training, we predict the existence of a latent confounder on any pair of variables Xi and Xj if lc(Xi , Xj ) is greater than τ . We choose τ = 0.4 but verify in Appendix C.3 that the method is not sensitive to the specific value of τ . As shown in Table 2, ENCO detects more than 95% of the latent confounders without any false positives. What is more, the few mistakes do not affect the detection of all other edges, which are recovered perfectly.

---

4.6. Real-World Inspired Data

Finally, we evaluate ENCO on causal graphs from the Bayesian Network Repository (BnLearn) (Scutari, 2010). The repository contains graphs inspired by real-world applications that are used as benchmarks in literature. In comparison to the synthetic graphs, the real-world graphs are sparser with a maximum of 6 parents per node and contain nodes with strongly peaked marginal distributions. They also include deterministic variables, making the task challenging even for small graphs.

 

We evaluate ENCO, SDI, and DCDI on 7 graphs with increasing sizes, see Table 3. We observe that ENCO recovers almost all real-world causal graphs without errors, independent of their size. In contrast, SDI suffers from more mistakes as the graphs become larger. An exception is pigs (Scutari, 2010), which has a maximum of 2 parents per node, and hence is easier to learn. The most challenging graph is diabetes (Andreassen et al., 1991) due to its large size and many deterministic variables. ENCO makes only two mistakes, showing that it can handle deterministic variables well. We discuss results on small sample sizes in Appendix C.5, observing similar trends. We conclude that ENCO can reliably perform structure learning on a wide variety of settings, including deterministic variables.

---

5. Conclusion

We propose ENCO, an efficient causal structure learning method leveraging observational and interventional data. Compared to previous work, ENCO models the edge orientations as separate parameters and uses an objective unconstrained with respect to acyclicity. This allows for easier optimization and low-variance gradient estimators while having convergence guarantees. As a consequence, the algorithm can efficiently scale to graphs that are at least one order of magnitude larger graphs than what was possible. Experiments corroborate the capabilities of ENCO compared to the state-of-the-art on an extensive array of settings on graph sizes, sizes of observational and interventional data, latent confounding, as well as on both partial and full intervention sets.

Limitations.

The convergence guarantees of ENCO require interventions on all variables, although experiments on fewer interventions have shown promising results. Future work includes investigating guarantee extensions of ENCO to this setting. A second limitation is that the orientations are missing transitivity: if X1 -> X2 and X2 -> X3, then X1 -> X3 must hold. A potential direction is incorporating transitive relations for improving convergence speed and results on fewer interventions.

---

A. Gradient Estimators

---

---

---