너와 나의 연결고리 (VI, EM, GMM, BGMM 흐름 정리!!)

1. Maximum likelihood (EM) Gaussian Mixture Model

Generative model: we specify p(data|parameters)

- The distribution that generated the data is a weighted sum of K Gaussians

- Each of the K Gaussians has its own mean and variance:  µk, Σk

- the likelihood for each data point is:

To generate samples from this model (given the parameters) we could:

1. Use some sampling method with the full probability distribution

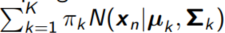
2. Reformulate the model with an additional variable z determining the class

 

=> Using a latent variable is much easier

---

2. GMM with a latent variable

- z is a one-of-K variable, so z_k = 1 if the class is k, and 0 otherwise

- If p(z_k = 1) = πk then marginalisation of z returns the model 

As a graphical model:

It is now easier to sample:

1. take a sample for z (using a uniform number generator)

2. take a sample for p(x|z). This is now a single Gaussian so use e.g. numpy.random.multivariate_normal

Example: K = 3, and π = (0.4, 0.5, 0.1)

sample a uniform random variable. Say u = 0.945. This falls in clas 3, so z = (0, 0, 1) Now generate sample from p(x|z3 = 1) = N(x|µ3, Σ3)

---

3. Fitting the GMM with EM

As with K-means:

- finding the expected values of the z_nk is possible, given all the parameters

- if z_nk are fixed, it is possible to find the best π, µ, Σ

This is an alternating algorithm similar to K-means, known as Expectation Maximization

---

4. Implementation

1. Initialize µk, Σk , πk

2. E-step: Evaluate responsibilities for every data point x_i using current parameters µk, Σk , πk:

 

3. M-step: Re-estimate parameters µk, Σk , πk using the current responsibilities r_ik (from E-step):

---

5. Shortcomings of EM GMM

- Sensitive to initialization

- Gives no indication of uncertainty in parameter values

- No easy way of determining the number of clusters

- Can fail due to problematic singularities (if a cluster has fewer points than dimensions the covariance is singular)

The Bayesian approach:

- Less sensitive to initialization

- Provides a distribution over parameter values, rather than a point estimate

- Provides the model evidence for comparison with other models

- Gives a principled way to determine the number of clusters

---

6. Bayesian Gaussian Mixture

- We want the means, covariances and mixture probabilities to be random variables

- For the mean  µ and covariance Σ, the natural choice is a Normal/Wishart:

- We specify the general shape W0, a constant that determines the variability of samples ν0, a center m0 and a constant b0 to specify how far the mean should be from m0 on average.

 

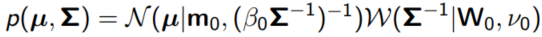
- We specify a (flat) Dirichlet prior for the mixture probabilities

 

While the likelihood is the same as before:

or

 

We now have a rather more complicated joint distribution:

 

From here we work with 

---

7. As a graphical model

---

8. Bayesian GMM inference

We need to integrate out all the unobserved variables:

As the unobserved variables are tangled up in the integrand, unfortunately such integration is analyltically intractable.

---

9. Why we need Bayesian models

- Point estimates can be misleading, and give no indication of uncertainty

- Bayesian methods are much more robust, especially with small data sets

- Bayesian methods incorporate prior beliefs in a principled way 

What stops us using Bayesian models?

- Typically intractable in all but the most simple cases

- That's it.

Variational inference is one way of making complex Bayesian models tractable!

---

10. Problem & Two options

Problem

We have:

- A generative model: 

- A task:

    1. find the model evidence:

    2. find the posterior over the latent variables:

We assume:

- Exact inference requires intractable integration

We want:

- To perform exact inference tractably...

- without simplifying the model itself

---

Two options

1. Approximate the exact model with finite samples

- pros:

  - Asymptotically correct

- cons:

  - Only finite time available

  - Usually scales poorly with dimension

  - Difficult to determine the quality of approximation

  - Often requires fine tuning to get good results

2. Use a simpler surrogate model which is as close as possible to the true model

- pros:

  - Can be fast and scalable to high dimension

  - Deterministic

- cons:

  - Not the true mode

  - Approximation might lose important dependencies

  - May still result in intractable integrals

---

11. Summary

Broadly:

- Sampling methods are approximate inference for the exact model

- Variational methods are exact inference for an aproximate model

 

The good news: the 'approximate model' can be gauranteed to be the best possible approximation, for a given approximating family

In general:

- High dimensional integration is very hard

- Optimization can be easier

---

12. ELBO

---

13. How to find q?

Cleary the best q(Z) would just be p(Z|X), but that defeats the point...

There are two specific approaches

- Mean field: we assume q factorizes

- Parametric family: we assume q belongs to some tractable family

---

14. Mean field

 

Mean field example: 2D Gaussian

---

15. Variational Inference for Bayesian GMM

---

What we need

---

The log joint

In some more detail...

In full glory...

where we dropped the constant terms

---

Start with Z

For z, terms needed:

Finding q*(Z)

The final result for q*(Z)

---

The other expectation

For π, terms needed:

Terms involving π

Result for q*(π)

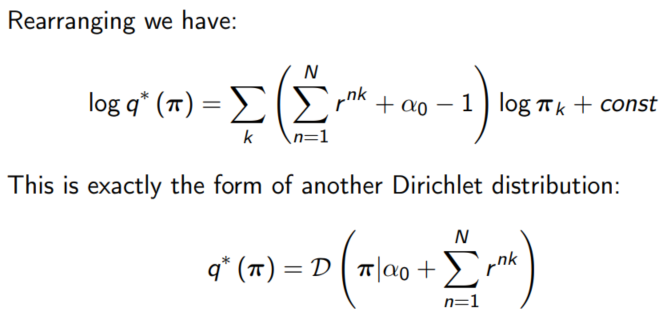
The remaining q(µ, Λ)

---

Conclusion

The important point is that all the posteriors can be found analytically, but they all depend on ρnk, which was defined as

 

Now we have the variational posteriors over π, µ, Λ  we can compute these terms analytically.

 

We have to proceed itereatively:

- q*(π) and q*(µ, Λ) depend on q(Z)

- q*(Z) depends on q(π) and q(µ, Λ)