-
[Implementation] MCMC*Generative Model/Generative Model 2024. 3. 24. 18:02
수식을 이해해도 다소 막연했던 알고리즘은 실제 구현을 해서 돌려보면, 와닿는 경우가 많다.
1. Gibbs Sampling
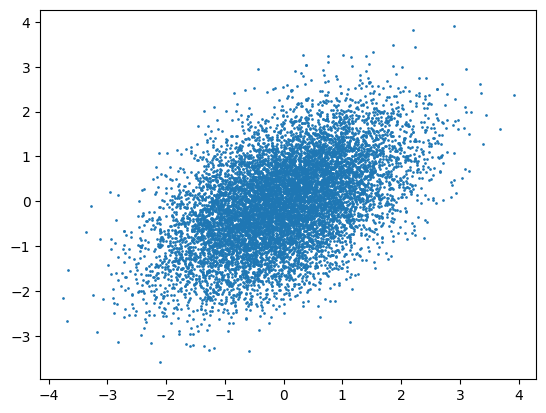
automatic_samples = np.random.multivariate_normal([0,0],[[1,0.5],[0.5,1]], 10000) plt.scatter(automatic_samples[:,0], automatic_samples[:,1], s=0.9); samples = {'x':[1], 'y':[-1]} num_samples = 10000 for _ in range(num_samples): curr_y = samples['y'][-1] new_x = np.random.normal(curr_y/2, np.sqrt(3/4)) new_y = np.random.normal(new_x/2, np.sqrt(3/4)) samples['x'].append(new_x) samples['y'].append(new_y) plt.scatter(samples['x'], samples['y'], s=0.9);
2. Accept-Reject (g(x)와 M을 달리하며 experiment)
# this function is the numerator of the target distribution def f(x): if x >= 1: return np.exp(-(x-1)/2) + np.exp(-(x-1)**2) else: return np.exp((x-1)/3) + np.exp((x-1)**3) # normal PDF def g(x, mu, sigma): return (1/(np.sqrt(2*np.pi) * sigma)) * np.exp(-0.5*((x-mu)/sigma)**2) NORM_CONST = 7.16556 x_vals = np.arange(-5,15, .1) f_vals = [f(x) for x in x_vals] p_vals = [f/NORM_CONST for f in f_vals] plt.figure(figsize=(9,4)) plt.plot(x_vals, f_vals) plt.plot(x_vals, p_vals) plt.legend(['f(x)', 'p(x)'], fontsize=19) plt.xlabel('x', fontsize=19) plt.ylabel('f(x)', fontsize=19) plt.axvline(1, color='r', linestyle='--') plt.show() TRUE_EXPECTATION = 1.94709 / NORM_CONST print(TRUE_EXPECTATION)
x_vals = np.arange(-30, 30, .1) f_vals = [f(x) for x in x_vals] g_vals = g(x_vals, 1, 4) M = 75 plt.figure(figsize=(9,4)) plt.plot(x_vals, f_vals) plt.plot(x_vals, M*g_vals) plt.xlabel('x', fontsize=19) plt.ylabel('Density', fontsize=19) plt.legend(['f(x)', 'Mg(x)'], fontsize=19) plt.title("M=%s" %M, fontsize=19) plt.show()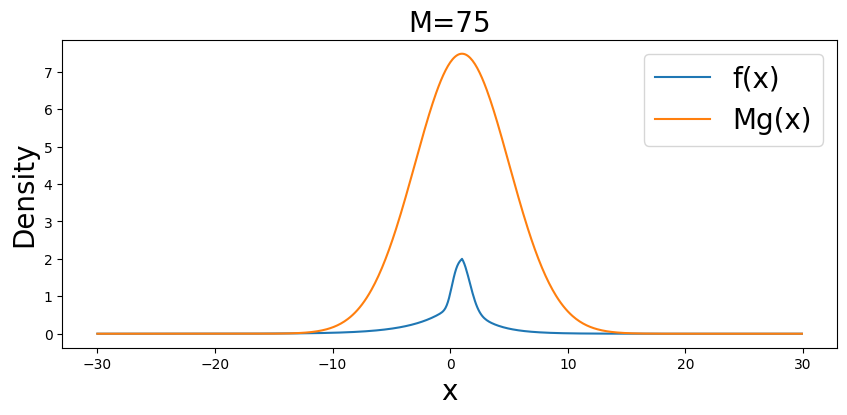
samples = [] N = 1000000 for _ in range(N): # get a candidate candidate = np.random.normal(1, 4) # calculate probability of accepting this sample prob_accept = f(candidate) / (M*g(candidate, 1, 4)) # accept sample with this probability if np.random.random() < prob_accept: samples.append(candidate) print("Num Samples Collected: %s" %len(samples)) print("Efficiency: %s"%round(len(samples) / N, 3)) plt.figure(figsize=(9,4)) plt.hist(samples, bins=200, density=True, alpha=.6) plt.xlabel('x', fontsize=19) plt.ylabel('Density', fontsize=19) plt.plot(x_vals, [f/NORM_CONST for f in f_vals], linewidth=1, color='r') plt.xlim(-15, 15) plt.title('Empirical Expectation Value: %s\nTrue Expectation Value: %s' %(round(np.mean(samples), 2), round(np.mean(TRUE_EXPECTATION), 2)), fontsize=19) plt.show()
3. Metropolis Algorithm with N(x_prev, 4)
samples = [1] num_accept = 0 for _ in range(N): # sample candidate from normal distribution candidate = np.random.normal(samples[-1], 4) # calculate probability of accepting this candidate prob = min(1, f(candidate) / f(samples[-1])) # accept with the calculated probability if np.random.random() < prob: samples.append(candidate) num_accept += 1 # otherwise report current sample again else: samples.append(samples[-1]) burn_in = 1000 retained_samples = samples[burn_in+1:] print("Num Samples Collected: %s" %len(retained_samples)) print("Efficiency: %s" %round(len(retained_samples) / N, 3)) print("Fraction Acceptances: %s" %(num_accept / N)) plt.figure(figsize=(9,4)) plt.hist(retained_samples, bins=200, density=True, alpha=.6) plt.xlabel('x',fontsize=19) plt.ylabel('Density', fontsize=19) plt.plot(x_vals, [f/NORM_CONST for f in f_vals], linewidth=1, color='r') plt.xlim(-15, 15) plt.title("Empirical Expectation Value: %s\nTrue Expectation Value: %s" %(round(np.mean(retained_samples), 2), round(np.mean(TRUE_EXPECTATION), 2)), fontsize=19) plt.show()
plt.figure(figsize=(6,6)) plt.scatter(retained_samples[:-1], retained_samples[1:], s=1) plt.xlabel('Previous Sample', fontsize=14) plt.ylabel('Current Sample', fontsize=14) corr = round(pearsonr(samples[:-1], samples[1:])[0], 2) plt.title('Correlation: %s' %corr, fontsize=19) plt.show()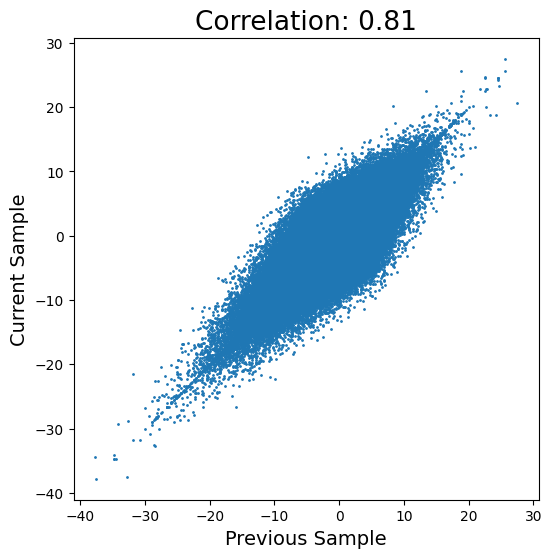
'*Generative Model > Generative Model' 카테고리의 다른 글
Rejection Sampling (0) 2024.03.27 너와 나의 연결고리 (VI, EM, GMM, BGMM 흐름 정리!!) (0) 2024.03.25 Introduction to Markov chains (0) 2024.03.24 Bayesian inference problem, MCMC and variational inference (0) 2024.03.23 The EM Algorithm Explained (0) 2024.03.19