How to Train Your Energy-Based Models

https://arxiv.org/pdf/2101.03288

---

Abstract

Energy-Based Models (EBMs), also known as non-normalized probabilistic models, specify probability density or mass functions up to an unknown normalizing constant. Unlike most other probabilistic models, EBMs do not place a restriction on the tractability of the normalizing constant, thus are more flexible to parameterize and can model a more expressive family of probability distributions. However, the unknown normalizing constant of EBMs makes training particularly difficult. Our goal is to provide a friendly introduction to modern approaches for EBM training. We start by explaining maximum likelihood training with Markov chain Monte Carlo (MCMC), and proceed to elaborate on MCMC-free approaches, including Score Matching (SM) and Noise Constrastive Estimation (NCE). We highlight theoretical connections among these three approaches, and end with a brief survey on alternative training methods, which are still under active research. Our tutorial is targeted at an audience with basic understanding of generative models who want to apply EBMs or start a research project in this direction.

---

1. Introduction

Probabilistic models with a tractable likelihood are a double-edged sword. On one hand, a tractable likelihood allows for straightforward comparison between models, and straightforward optimization of the model parameters w.r.t. the log-likelihood of the data. Through tractable models such as autoregressive (Graves, 2013; Germain et al., 2015; Van Oord et al., 2016) or flow-based generative models (Dinh et al., 2014, 2016; Rezende and Mohamed, 2015), we can learn flexible models of high-dimensional data. In some cases even though the likelihood is not completely tractable, we can often compute and optimize a tractable lower bound of the likelihood, as in the framework of variational autoencoders (Kingma and Welling, 2014; Rezende et al., 2014).

 

Still, the set of models with a tractable likelihood is constrained. Models with a tractable likelihood need to be of a certain form: for example, in case of autoregressive models, the model distribution is factorized as a product of conditional distributions, and in flow-based generative models the data is modeled as an invertible transformation of a base distribution. In case of variational autoencoders, the data must be modeled as a directed latent-variable model. A tractable likelihood is related to the fact that these models assume that exact synthesis of pseudo-data from the model can be done with a specified, tractable procedure. These assumptions are not always natural.

 

Energy-based models (EBM) are much less restrictive in functional form: instead of specifying a normalized probability, they only specify the unnormalized negative log-probability, called the energy function. Since the energy function does not need to integrate to one, it can be parameterized with any nonlinear regression function. In the framework of EBMs, density estimation is thus basically reduced to a nonlinear regression problem. One is generally free to choose any nonlinear regression function as the energy function, as long as it remains normalizable in principle. It is thus straightforward to leverage advances in architectures originally developed for classification or regression, and one may choose special-purpose architectures that make sense for the type of data at hand. For example, If the data are graphs (such as molecules) then one could use graph neural networks (Scarselli et al., 2008); if the data are spherical images one can in principle use spherical CNNs (Cohen et al., 2018). As such, EBMs have found wide applications in many fields of machine learning, including, among others, image generation (Ngiam et al., 2011; Xie et al., 2016; Du and Mordatch, 2019), discriminative learning (Grathwohl et al., 2020b; Gustafsson et al., 2020a,b), natural language processing (Mikolov et al., 2013; Deng et al., 2020), density estimation (Wenliang et al., 2019; Song et al., 2019) and reinforcement learning (Haarnoja et al., 2017, 2018).  

 

Although this flexibility of EBMs can provide significant modeling advantages, both computation of the exact likelihood and exact synthesis of samples from these models are generally intractable, which makes training especially difficult. There are three major ways for training EBMs: (i) maximum likelihood training with MCMC sampling; (ii) Score Matching (SM); and (iii) Noise Constrastive Estimation (NCE). We will elaborate on these methods in order, explain their relationships to each other, and conclude by an overview to other directions for EBM training.

---

2. Energy-Based Models (EBMs)

For simplicity we will assume unconditional Energy-Based Models over a single dependent variable x. It is relatively straightforward to extend the models and estimation procedures to the case with multiple dependent variables, or with conditioning variables. The density given by an EBM is

---

3. Maximum Likelihood Training with MCMC

The de facto standard for learning probabilistic models from i.i.d. data is maximum likelihood estimation (MLE). Let pθ(x) be a probabilistic model parameterized by θ, and pdata(x) be the underlying data distribution of a dataset. We can fit pθ(x) to pdata(x) by maximizing the expected log-likelihood function over the data distribution, defined by

 

as a function of θ. Here the expectation can be easily estimated with samples from the dataset. Maximizing likelihood is equivalent to minimizing the KL divergence between pdata(x) and pθ(x), because

 

where the second equality holds because Ex∼pdata(x) [log pdata(x)] does not depend on θ.

 

We cannot directly compute the likelihood of an EBM as in the maximum likelihood approach due to the intractable normalizing constant Zθ. Nevertheless, we can still estimate the gradient of the log-likelihood with MCMC approaches, allowing for likelihood maximization with gradient ascent (Younes, 1999). In particular, the gradient of the log-probability of an EBM (Eq. (1)) decomposes as a sum of two terms:

 

The first gradient term, −∇θEθ(x), is straightforward to evaluate with automatic differentiation. The challenge is in approximating the second gradient term, ∇θ log Zθ, which is intractable to compute exactly. This gradient term can be rewritten as the following expectation:

 

where steps (i) and (ii) are due to the chain rule of gradients, and (iii) and (iv) are from definitions in Eqs. (1) and (2). Thus, we can obtain an unbiased one-sample Monte Carlo estimate of the log-likelihood gradient by

where x˜ ∼ pθ(x), i.e., a random sample from the distribution over x given by the EBM. Therefore, as long as we can draw random samples from the model, we have access to an unbiased Monte Carlo estimate of the log-likelihood gradient, allowing us to optimize the parameters with stochastic gradient ascent.

 

Since drawing random samples is far from being trivial, much of the literature has focused on methods for efficient MCMC sampling from EBMs. Some efficient MCMC methods, such as Langevin MCMC (Parisi, 1981; Grenander and Miller, 1994) and Hamiltonian Monte Carlo (Duane et al., 1987; Neal et al., 2011), make use of the fact that the gradient of the log-probability w.r.t. x (a.k.a., score) is equal to the (negative) gradient of the energy, therefore easy to calculate:

 

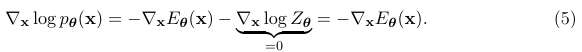
For example, when using Langevin MCMC to sample from pθ(x), we first draw an initial sample x 0 from a simple prior distribution, and then simulate an (overdamped) Langevin diffusion process for K steps with step size ⲉ > 0:

 

When ⲉ → 0 and K → ∞, xK is guaranteed to distribute as pθ(x) under some regularity conditions. In practice we have to use a small finite ⲉ, but the discretization error is typically negligible, or can be corrected with a Metropolis-Hastings (Hastings, 1970) step, leading to the Metropolis-Adjusted Langevin Algorithm (Besag, 1994).

 

Running MCMC till convergence to obtain a sample x ∼ pθ(x) can be computationally expensive. Therefore we typically need approximation to make MCMC-based learning of EBMs practical. One popular method for doing so is Contrastive Divergence (CD) (Hinton, 2002). In CD, one initializes the MCMC chain from the datapoint x, and perform a fixed number of MCMC steps; typically fewer than required for convergence of the MCMC chain. One variant of CD that sometimes performs better is persistent CD (Tieleman, 2008), where a single MCMC chain with a persistent state is employed to sample from the EBM. In persistent CD, we do not restart the MCMC chain when training on a new datapoint; rather, we carry over the state of the previous MCMC chain and use it to initialize a new MCMC chain for the next training step. This method can be further improved by keeping multiple historical states of the MCMC chain in a replay buffer and initialize new MCMC chains by randomly sampling from it (Du and Mordatch, 2019). Other variants of CD include mean field CD (Welling and Hinton, 2002), and multi-grid CD (Gao et al., 2018).

 

EBMs trained with CD may not capture the data distribution faithfully, since truncated MCMC can lead to biased gradient updates that hurt the learning dynamics (Schulz et al., 2010; Fischer and Igel, 2010; Nijkamp et al., 2019). There are several methods that focus on removing this bias for improved MCMC training. For example, one line of work proposes unbiased estimators of the gradient through coupled MCMC (Jacob et al., 2017; Qiu et al., 2019); and Du et al. (2020) propose to reduce the bias by differentiating through the MCMC sampling algorithm and estimating an entropy correction term.

---

4. Score Matching (SM)

If two continuously differentiable real-valued functions f(x) and g(x) have equal first derivatives everywhere, then f(x) ≡ g(x) + constant. When f(x) and g(x) are log probability density functions (PDFs) with equal first derivatives, the normalization requirement (Eq. (1)) implies that R exp(f(x))dx = R exp(g(x))dx = 1, and therefore f(x) ≡ g(x). As a result, one can learn an EBM by (approximately) matching the first derivatives of its log-PDF to the first derivatives of the log-PDF of the data distribution. If they match, then the EBM captures the data distribution exactly. The first-order gradient function of a log-PDF is also called the score of that distribution. For training EBMs, it is useful to transform the equivalence of distributions to the equivalence of scores, because the score of an EBM can be easily obtained by ∇x log pθ(x) = −∇xEθ(x) (recall from Eq. (5)) which does not involve the typically intractable normalizing constant Zθ.

 

Let pdata(x) be the underlying data distribution, from which we have a finite number of i.i.d. samples but do not know its PDF. The basic Score Matching (Hyvärinen, 2005) (SM) objective minimizes a discrepancy between two distributions called the Fisher divergence:

 

The expectation w.r.t. pdata(x), in this objective and its variants below, admits a trivial unbiased Monte Carlo estimator using the empirical mean of samples x ∼ pdata(x). However, the second term of Eq. (7) is generally impractical to calculate since it requires knowing ∇x log pdata(x). Hyvärinen (2005) shows that under certain regularity conditions, the Fisher divergence can be rewritten using integration by parts, with second derivatives of Eθ(x) replacing the unknown first derivatives of pdata(x):

 

where d is the dimensionality of x. The constant does not affect optimization and thus can be dropped for training. It is shown by Hyvärinen (2005) that estimators based on Score Matching are consistent under some regularity conditions, meaning that the parameter estimator obtained by minimizing Eq. (7) converges to the true parameters in the limit of infinite data.

 

An important downside of the objective Eq. (8) is that, in general, computation of full second derivatives is quadratic in the dimensionality d, thus does not scale to high dimensionality. Although SM only requires the trace of the Hessian, it is still expensive to compute even with modern hardware and automatic differentiation packages (Martens et al., 2012). For this reason, the implicit SM formulation of Eq. (8) has only been applied to relatively simple energy functions where computation of the second derivatives is tractable.

 

Score Matching assumes a continuous data distribution with positive density over the space, but it can be generalized to discrete or bounded data distributions (Hyvärinen, 2007; Lyu, 2012). It is also possible to consider higher-order gradients of log-PDFs beyond first derivatives (Parry et al., 2012).

---

4.1. Denoising Score Matching (DSM)

The Score Matching objective in Eq. (8) requires several regularity conditions for log pdata(x), e.g., it should be continuously differentiable and finite everywhere. However, these conditions may not always hold in practice. For example, a distribution of digital images is typically discrete and bounded, because the values of pixels are restricted to the range {0, 1, · · · , 255}. Therefore, log pdata(x) in this case is discontinuous and is negative infinity outside the range, and therefore SM is not directly applicable.

 

To alleviate this difficulty, one can add a bit of noise to each datapoint: x˜ = x + ⲉ. As long as the noise distribution p(ⲉ) is smooth, the resulting noisy data distribution q(x˜) = R q(x˜ | x)pdata(x)dx is also smooth, and thus the Fisher divergence DF (q(x˜) k pθ(x˜)) is a proper objective. Kingma and LeCun (2010) showed that the objective with noisy data can be approximated by the noiseless Score Matching objective of Eq. (8) plus a regularization term; this regularization makes Score Matching applicable to a wider range of data distributions, but still requires expensive second-order derivatives.

 

Vincent (2011) propose one elegant and scalable solution to the above difficulty, by showing that:

 

where the expectation is again approximated by the empirical average of samples, thus completely avoiding both the unknown term pdata(x) and computationally expensive secondorder derivatives. The constant term does not affect optimization and can be ignored without changing the optimal solution. This estimation method is called Denoising Score Matching (DSM) by Vincent (2011). Similar formulations are also explored by Raphan and Simoncelli (2007, 2011) and can be traced back to Tweedie’s formula (1956) and Stein’s Unbiased Risk Estimation (Stein, 1981).

 

The major drawback of adding noise to data arises when pdata(x) is already a well-behaved distribution that satisfies the regularity conditions required by Score Matching. In this case, DF (q(x˜) k pθ(x˜)) 6= DF (pdata(x) k pθ(x)), and DSM is not a consistent objective because the optimal EBM matches the noisy distribution q(x˜), not pdata(x). This inconsistency becomes non-negligible when q(x˜) significantly differs from pdata(x).

 

One way to attenuate the inconsistency of DSM is to choose q ≈ pdata, i.e., use a small noise perturbation. However, this often significantly increases the variance of objective values and hinders optimization. As an example, suppose q(x˜ | x) = N (x˜ | x, σ2 I) and σ ≈ 0. The corresponding DSM objective is

---

4.2. Sliced Score Matching (SSM)

By adding noise to data, DSM avoids the expensive computation of second-order derivatives. However, as mentioned before, the optimal EBM that minimizes the DSM objective corresponds to the distribution of noise-perturbed data q(x˜), not the original noise-free data distribution pdata(x). In other words, DSM does not give a consistent estimator of the data distribution, i.e., one cannot directly obtain an EBM that exactly matches the data distribution even with unlimited data.

 

Sliced Score Matching (SSM) (Song et al., 2019) is one alternative to Denoising Score Matching that is both consistent and computationally efficient. Instead of minimizing the Fisher divergence between two vector-valued scores, SSM randomly samples a projection vector v, takes the inner product between v and the two scores, and then compare the resulting two scalars. More specifically, Sliced Score Matching minimizes the following divergence called the sliced Fisher divergence

 

where p(v) denotes a projection distribution such that Ep(v) [vvT] is positive definite. Similar to Fisher divergence, sliced Fisher divergence has an implicit form that does not involve the unknown ∇x log pdata(x), which is given by

 

All expectations in the above objective can be estimated with empirical means, and again the constant term can be removed without affecting training. The second term involves second-order derivatives of Eθ(x), but contrary to SM, it can be computed efficiently with a cost linear in the dimensionality d. This is because

The above objective Eq. (17) can also be obtained by approximating the sum of secondorder gradients in the standard SM objective (Eq. (8)) with the Skilling-Hutchinson trace estimator (Skilling, 1989; Hutchinson, 1989). It often (but not always) has lower variance than Eq. (15), and can perform better in some applications (Song et al., 2019).

---

4.3. Connection to Contrastive Divergence

Though Score Matching and Contrastive Divergence are seemingly very different approaches, they are closely connected to each other. In fact, Score Matching can be viewed as a special instance of Contrastive Divergence in the limit of a particular MCMC sampler (Hyvarinen, 2007). Moreover, the Fisher divergence optimized by Score Matching is related to the derivative of KL divergence (Cover, 1999), which is the underlying objective of Contrastive Divergence.

---

4.4. Score-Based Generative Models

 

One typical application of EBMs is creating new samples that are similar to training data. Towards this end, we can first train an EBM with Score Matching, and then sample from it with MCMC approaches. Many efficient sampling methods for EBMs, such as Langevin MCMC, rely on just the score of the EBM (see Eq. (6)). In addition, Score Matching objectives (Eqs. (8), (10) and (15)) depend sorely on the scores of EBMs. Therefore, we only need a model for score when training with Score Matching and sampling with score-based MCMC, and do not have to model the energy explicitly. By building such a score model, we save the gradient computation of EBMs and can make training and sampling more efficient. These kind of models are named score-based generative models (Song and Ermon, 2019, 2020; Song et al., 2021).

 

Score Matching has difficulty in estimating the relative weights of two modes separated by large low-density regions (Wenliang et al., 2019; Song and Ermon, 2019), which can have an important negative impact on sample generation. As an example, suppose pdata(x) = πp0(x) + (1 − π)p1(x). Let S0 := {x | p0(x) > 0} and S1 := {x | p1(x) > 0} be the supports of p0(x) and p1(x) respectively. When they are disjoint from each other, the score of pdata(x) is given by

 

which does not depend on the weight π. Since Score Matching trains an EBM by matching its score to the score of data, ∇x log pdata(x), which contains no information of π in this case, it is impossible for the learned EBM to recover the correct weight of p0(x) or p1(x). In practice, the regularity conditions of Score Matching actually require pdata(x) > 0 everywhere, so S0 and S1 cannot be completely disjoint from each other, but when they are close to being mutually disjoint (which often happens in real data especially in high-dimensional space), it will be very hard to learn the weights accurately with Score Matching. When the weights are not accurate, samples will concentrate around different data modes with an inappropriate portion, leading to worse sample quality.

 

Song and Ermon (2019, 2020) and Song et al. (2021) overcome this difficulty by perturbing training data with different scales of noise, and learn a score model for each scale. For a large noise perturbation, different modes are connected due to added noise, and estimated weights between them are therefore accurate. For a small noise perturbation, different modes are more disconnected, but the noise-perturbed distribution is closer to the original unperturbed data distribution. Using a sampling method such as annealed Langevin dynamics (Song and Ermon, 2019, 2020; Song et al., 2021) or leveraging reverse diffusion processes (Sohl-Dickstein et al., 2015; Ho et al., 2020; Song et al., 2021), we can sample from the most noise-perturbed distribution first, then smoothly reduce the magnitude of noise scales until reaching the smallest one. This procedure helps combine information from all noise scales, and maintains the correct portion of modes from larger noise perturbations when sampling from smaller ones. In practice, all score models share weights and are implemented with a single neural network conditioned on the noise scale, named a Noise-Conditional Score Network. Scores of different scales are estimated by training a mixture of Score Matching objectives, one per noise scale. This method are amongst the best generative modeling approaches for high-resolution image generation (see samples in Fig. 1), audio synthesis (Chen et al., 2020; Kong et al., 2020), and shape generation (Cai et al., 2020).

---

5. Noise Contrastive Estimation

A third principle for learning the parameters of EBMs is Noise Contrastive Estimation (NCE), introduced by Gutmann and Hyvärinen (2010). It is based on the idea that we can learn an Energy-Based Model by contrasting it with another distribution with known density.

 

Let pdata(x) be our data distribution, and let pn(x) be a chosen distribution with known density, called a noise distribution. This noise distribution is usually simple and has a tractable PDF, like N (0, I), such that we can compute the PDF and generate samples from it efficiently. Strategies exist to learn the noise distribution, as referenced below. Let y be a binary variable with Bernoulli distribution, which we use to define a mixture distribution of noise and data: pn,data(x) = p(y = 0)pn(x) + p(y = 1)pdata(x). According to the Bayes’ rule, given a sample x from this mixture, the posterior probability of y = 0 is

 

which can be solved using stochastic gradient ascent. Just like any other deep classifier, when the model is sufficiently powerful, pn,θ∗ (y | x) will match pn,data(y | x) at the optimum. In that case:

 

Consequently, Eθ∗ (x) is an unnormalized energy function that matches the data distribution pdata(x), and Zθ∗ is the corresponding normalizing constant.

 

As one unique feature that Contrastive Divergence and Score Matching do not have, NCE provides the normalizing constant of an Energy-Based Model as a by-product of its training procedure. When the EBM is very expressive, e.g., a deep neural network with many parameters, we can assume it is able to approximate a normalized probability density and absorb Zθ into the parameters of Eθ(x) (Mnih and Teh, 2012), or equivalently, fixing Zθ = 1. The resulting EBM trained with NCE will be self-normalized, i.e., having a normalizing constant close to 1.

 

In practice, choosing the right noise distribution pn(x) is critical to the success of NCE, especially for structured and high-dimensional data. As argued in Gutmann and Hirayama (2012), NCE works the best when the noise distribution is close to the data distribution (but not exactly the same). Many methods have been proposed to automatically tune the noise distribution, such as Adversarial Contrastive Estimation (Bose et al., 2018), Conditional NCE (Ceylan and Gutmann, 2018) and Flow Contrastive Estimation (Gao et al., 2020). NCE can be further generalized using Bregman divergences (Gutmann and Hirayama, 2012), where the formulation introduced here reduces to a special case.

---

5.1. Connection to Score Matching

Noise Contrastive Estimation provides a family of objectives that vary for different pn(x) and ν. This flexibility may allow adaptation to special properties of a task with hand-tuned pn(x) and ν, and may also give a unified perspective for different approaches. In particular, when using an appropriate pn(x) and a slightly different parameterization of pn,θ(y | x), we can recover Score Matching from NCE (Gutmann and Hirayama, 2012).

 

For example, we choose the noise distribution pn(x) to be a perturbed data distribution: given a small (deterministic) vector v, let pn(x) = pdata(x − v). It is efficient to sample from this pn(x), since we can first draw any datapoint x 0 ∼ pdata(x 0 ) and then compute x = x 0 + v. It is, however, difficult to evaluate the density of pn(x) because pdata(x) is unknown. Since the original parameterization of pn,θ(y | x) in NCE (Eq. (19)) depends on the PDF of pn(x), we cannot directly apply the standard NCE objective. Instead, we replace pn(x) with pθ(x − v) and parameterize pn,θ(y = 0 | x) with the following form

---

6. Conclusion

We reviewed some of the modern approaches for EBM training. In particular, we focused on maximum likelihood estimation with MCMC sampling, Score Matching, and Noise Contrastive Estimation. We emphasized their mutual connections, and concluded by a short review on other EBM training approaches that do not directly fall into these three categories. The contents of this tutorial is of course limited to the authors’ knowledge and bias in the field; we did not cover many other important aspects of EBMs, including EBMs with latent variables, and various downstream applications of EBMs. Training techniques are crucial to problem solving with EBMs, and will remain an active direction for future research.