-
Variational Inference with Normalizing Flows on MNIST*Generative Model/Generative Model 2024. 4. 30. 22:37
https://towardsdatascience.com/variational-inference-with-normalizing-flows-on-mnist-9258bbcf8810
Introduction
In this post, I will explain what normalizing flows are and how they can be used in variational inference and designing generative models. The materials of this article mostly comes from [Rezende and Mohamed, 2015], which I believe is the first paper that introduces the concept of flow-based models (the title of this article is almost identical to the paper’s title). There are a lot of other interesting papers that followed up this one and used flow-based models to solve other interesting tasks. However, in this post my focus is just on the first paper and on covering the most fundamental concepts.
I have tried to explain how these models work step-by-step and there is a PyTorch code snippet accompanying each step. The code of the model and visualizations are all available in this Github repo.
Before getting into normalizing flows, it is helpful to review what variational inference is and how normalizing flows relate to it.
What is variational inference?
Assume that we have a set of observations x¹, x², …, xⁿ, where they are i.i.d. samples of a distribution p(x) which we are not aware of (these samples are not necessarily in 1-D space and can be multidimensional). Also, assume that there are a set of hypothetical variables z¹, z², …, zⁿ that are behind generating these data samples. In fact, to generate a sample of the data, first a latent variable is sampled from a distribution p(z) and then it is used to compute a data sample x which we observe. As z’s are not observable in the real world they are called latent variables.
We can mathematically specify our model with the joint distribution of x and z , i.e. P(x, z). This is a sufficient representation of our model and one can compute P(x) and P(z) from this joint distribution. We usually like to parameterize distributions with some parameters θ — where most of the times θ are the parameters of a neural network. Therefore, we can make the dependence on the parameters explicit in our notation by writing the distribution as P(x, z ; θ). Now, similar to most of the problems in machine learning, our objective is to learn the parameters of the model. The most common way of doing so it to maximize the log likelihood of the observed data (i.e. x’s) under our model. To accomplish this, we need to be able to compute the marginal likelihood P(x ; θ) and for that, we have to marginalize the latent variables out by summing/integrating over all possible values of them. But that is unimaginably expensive most of the times as there are lots of z’s! Hmmmm…..If it is not possible to compute a simple likelihood then how can we do maximum likelihood training?
It turns out there is one possible answer to this question:
1) Introduce an auxiliary distribution, such as q(z|x ; ϕ), which we can easily compute and work with. This distribution serves as an approximate to the intractable posterior p(z|x ; θ) and thus is called the approximate posterior or variational distribution.
2) Instead of maximizing the log-likelihood directly, we maximize a lower bound of it called ELBO which is given by the following formula:

Eq. 15 of [1] ELBO is -F(x) in the above equation. It can be easily proved that maximizing ELBO is equivalent to maximizing the log-likelihood (or minimizing negative log-likelihood is equivalent to minimizing negative ELBO). Therefore our new objective is this:
Learn the parameters of the model, i.e. θ, and the parameters of the variational distribution, i.e. , jointly by maximizing ELBO.
In other words, variational parameters enable us to learn the model’s parameters too. One elegant way of doing this is using variational auto encoders. However, if you are familiar with VAEs, you know that they suffer from one drawback: the variational family is in most of the cases too simple and not expressive enough (usually it is a multivariate Gaussian) and cannot approximate arbitrarily complex distributions. This is where Normalizing flows come and help us overcome this problem.
What is Normalizing Flow?
Normalizing flows are models that can start from a simple distribution and approximate a complex distribution. They do this by transforming the initial distribution multiple times with some functions until the distribution gets complex enough. To transform a distribution we can use an invertible function f. From the change of variables formula we know that the pdf of a transformed variable can be computed as follows (Eq. 5 of [1]):
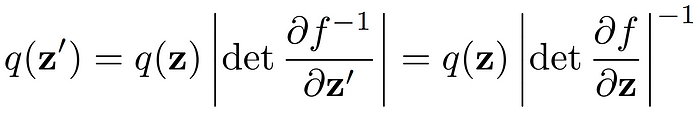
Now, If we stack k such invertible transforms sequentially, the density of the last variable can be derived as follows (Eq. 6 and 7 of [1]):

Eq. 6 and 7 of [1] We will see the log probability of this last variable in the loss we define for our generative model later.
One caveat here is that these transformations must be efficient and easy to compute, especially given the fact that there is a term containing determinants in the density formula (determinants are usually are hard to compute). Fortunately, [1] proposes two family of transformations where their determinants can be computed easily. They are also powerful enough that we can start from a simple distribution and create a very complex distribution just using these two transforms.
1. Planar flow: the formula for this transform is as follows:

This transform takes a D-dimensional vector and expands/contracts this vector in the direction perpendicular to the hyperplane specified by the weight W and bias b. Planar flow transforms can be implemented in PyTorch as follows:
class PlanarFlow(nn.Module): def __init__(self, D, activation=torch.tanh): super().__init__() self.D = D self.w = nn.Parameter(torch.empty(D)) self.b = nn.Parameter(torch.empty(1)) self.u = nn.Parameter(torch.empty(D)) self.activation = activation self.activation_derivative = ACTIVATION_DERIVATIVES[activation] nn.init.normal_(self.w) nn.init.normal_(self.u) nn.init.normal_(self.b) def forward(self, z: torch.Tensor): lin = (z @ self.w + self.b).unsqueeze(1) # shape: (B, 1) f = z + self.u * self.activation(lin) # shape: (B, D) phi = self.activation_derivative(lin) * self.w # shape: (B, D) log_det = torch.log(torch.abs(1 + phi @ self.u)) # shape: (B,) return f, log_detTo better understand how this layer performs, I have visualized the input and output of a simple flow layer in the 2D space with ten different values for |u|.
The result is shown in the following figure where the blue points represents the initial distribution and the red points are the transformed version of them. Also, each point is connected to its transformed counterpart with a solid line. We can easily see that the lines are all parallel and perpendicular to the hyperplane w.x+b=0 which is simply the line x+y=0.

Visualization of Planar-flow outputs for different vectors u 2. Radial flow: The second family of transforms is called Radial flow and can be described with the following formula:

This transform expands or contracts the initial distribution around a single point in the space and can be implemented in PyTorch as follows:
class RadialFlow(nn.Module): def __init__(self, D, activation=torch.tanh): super().__init__() self.z0 = nn.Parameter(torch.empty(D)) self.log_alpha = nn.Parameter(torch.empty(1)) self.beta = nn.Parameter(torch.empty(1)) self.activation = activation self.activation_derivative = ACTIVATION_DERIVATIVES[activation] self.D = D nn.init.normal_(self.z0) nn.init.normal_(self.log_alpha) nn.init.normal_(self.beta) def forward(self, z: torch.Tensor): z_sub = z - self.z0 alpha = torch.exp(self.log_alpha) r = torch.norm(z_sub) h = 1 / (alpha + r) f = z + self.beta * h * z_sub log_det = (self.D - 1) * torch.log(1 + self.beta * h) + \ torch.log(1 + self.beta * h + self.beta - self.beta * r / (alpha + r) ** 2) return f, log_detAgain, we can plot a visualization of this transform in the 2-D space with different values of β and the origin (0, 0) as the center of transform. Similar to the previous visualization, blue points represent the initial distribution and red points represent the points after applying the transform (Note that the lines meet at the origin which is the center of transform):

Visualization of radial-flow outputs with different values of β We can use a sequence of these two layers and transform a simple initial distribution (e.g. multivariate Gaussian) to a complex distribution (e.g. multimodal distributions).
Implementation of Flow-based Generative Models
To implement a generative model based on normalizing flows, we can use the following architecture proposed by the paper (Fig. 2 of [1]):

Architecture of the flow-based generative model (Fig. 2 of [1]) This model consists of the following three modules and we will implement them one by one in PyTorch.
1. Encoder: First, there is an encoder which gets the observed input x and outputs the mean (e.g. μ) and log-std (e.g. log(σ)) of the first variable in the flow of random variables, i.e. Z₀. It is worth to note that this encoder is similar to the encoders of variational auto-encoders.
class FCNEncoder(nn.Module): def __init__(self, hidden_sizes: List[int], dim_input: int, activation=nn.ReLU()): super().__init__() hidden_sizes = [dim_input] + hidden_sizes self.net = [] for i in range(len(hidden_sizes) - 1): self.net.append(nn.Linear(hidden_sizes[i], hidden_sizes[i+1])) self.net.append(nn.ReLU()) self.net = nn.Sequential(*self.net) def forward(self, x): return self.net(x)2. Flow-model: After the encoder there are a stack of flow layers which transforms the samples from the first distribution (i.e. Z₀ from the distribution q₀) to the samples Zₖ from the complex distribution qₖ. Note that Zₖ is the main latent variable that generates the data and we have used all the encoder+flow layers just to infer Zₖ. Therefore, as specified in the figure of the architecture, we can call these two modules together the inference network. Following is the implementation of flow-model:
class FlowModel(nn.Module): def __init__(self, flows: List[str], D: int, activation=torch.tanh): super().__init__() self.prior = MultivariateNormal(torch.zeros(D), torch.eye(D)) self.net = [] for i in range(len(flows)): layer_class = eval(flows[i]) self.net.append(layer_class(D, activation)) self.net = nn.Sequential(*self.net) self.D = D def forward(self, mu: torch.Tensor, log_sigma: torch.Tensor): """ mu: tensor with shape (batch_size, D) sigma: tensor with shape (batch_size, D) """ sigma = torch.exp(log_sigma) batch_size = mu.shape[0] samples = self.prior.sample(torch.Size([batch_size])) z = samples * sigma + mu z0 = z.clone().detach() log_prob_z0 = torch.sum( -0.5 * torch.log(torch.tensor(2 * math.pi)) - log_sigma - 0.5 * ((z - mu) / sigma) ** 2, axis=1) log_det = torch.zeros((batch_size,)) for layer in self.net: z, ld = layer(z) log_det += ld log_prob_zk = torch.sum( -0.5 * (torch.log(torch.tensor(2 * math.pi)) + z ** 2), axis=1) return z, log_prob_z0, log_prob_zk, log_detAs seen in the above code, we have utilized the reparameterization trick in the implementation of the flow-model where we move the stochasticity to samples from another standard Gaussian distribution, such as ε, and then use σ*ε+μ as the initial samples Z₀. With this trick, we will be able to pass the gradient to the encoder network and train it too.
Also, we accumulate the log determinants computed by each layer in the log_det variable. The model outputs this variable which will later be used in computing the loss. The same argument holds for the log probability of Z₀ and Zₖ where they also appear in the loss we calculate.
3. Decoder: Finally, The decoder takes the latent variable Zₖ and models P(x|zₖ) (or the unnormalized version of it which are sometimes called logits). Again, it is similar to the decoder of variational auto-encoders and can be implemented as a fully connected network:
class FCNDecoder(nn.Module): def __init__(self, hidden_sizes: List[int], dim_input: int, activation=nn.ReLU()): super().__init__() hidden_sizes = [dim_input] + hidden_sizes self.net = [] for i in range(len(hidden_sizes) - 1): self.net.append(nn.Linear(hidden_sizes[i], hidden_sizes[i+1])) self.net.append(nn.ReLU()) self.net = nn.Sequential(*self.net) def forward(self, z: torch.Tensor): return self.net(z)Now, let’s specify what θ and ϕ are here. θ is the parameters of our model of the real world which consists of the parameters of the prior p(z) and the parameters of P(x|zₖ). Our prior is standard multivariate Gaussian and has no parameters. Therefore the only parameters of our model are the parameters of P(x|zₖ) which is our decoder. ϕ is the variational parameters which consists of all the parameters that helped us approximate true posterior distribution from the data x. Therefore it consists of the parameters of the encoder and the flow-model.
Loss
One of the most important parts of training any machine learning model is the loss function. As stated by the paper, we will optimize the negative ELBO as our objective which is computed via the following formula (Eq. 15 of [1]):
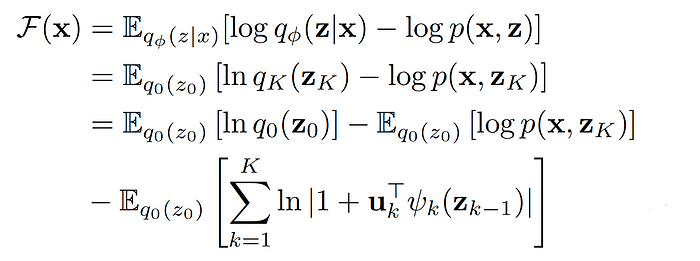
The term inside the first expectation, ln q₀(z₀), is the log probability of the initial variational samples which was one of the outputs of the flow-model. The term in the second expectation, log p(x, zₖ), can also be written as
log p(x|zₖ) + log p(zₖ). In this equivalent expression, the first term is the normalized output of the decoder (we will normalize the output of the decoder using the sigmoid function) and the second term is the log probability of zₖ which was another output of the flow-model. Finally the term inside the third expectation is the log_det output of the flow-model. Note that we can estimate the expectation stochastically by taking the average over the mini-batch. Here is the computation of the final loss in PyTorch (D is the dimension of random variables):out = encoder(X_batch.view(-1, 784).float()) mu, log_sigma = out[:, :D], out[:, D:] z_k, log_prob_z0, log_prob_zk, log_det = flow_model(mu, log_sigma) x_hat = decoder(z_k) loss = torch.mean(log_prob_z0) + loss_fn(x_hat, X_batch.view(-1, 784).float()) - torch.mean(log_prob_zk) - torch.mean(log_det)
Train the model on Binarized MNIST Dataset
Finally, we can train a generative model with the objective defined above on the Binarized MNIST dataset. Here are some sample from this dataset:

Binarized MNIST dataset The only thing we have to do is to define a model, load the data as mini-batches, define an optimizer (for which we use Adam), and code a train loop:
D = 40 mnist_data = BinarizedMNIST('datasets/bin_mnist.npy') data_loader = torch.utils.data.DataLoader(mnist_data, batch_size=32, shuffle=True, num_workers=0) encoder = FCNEncoder(hidden_sizes=[128, 64, 2*D], dim_input=28*28) flow_model = FlowModel(flows=['PlanarFlow'] * 10, D=40) decoder = FCNDecoder(hidden_sizes=[64, 128, 784], dim_input=40) loss_fn = BCEWithLogitsLoss() for i, X_batch in enumerate(data_loader): optimizer.zero_grad() out = encoder(X_batch.view(-1, 784).float()) mu, log_sigma = out[:, :40], out[:, 40:] z_k, log_prob_z0, log_prob_zk, log_det = flow_model(mu, log_sigma) x_hat = decoder(z_k) loss = torch.mean(log_prob_z0) + loss_fn(x_hat, X_batch.view(-1, 784).float()) - torch.mean(log_prob_zk) - torch.mean(log_det) if i % 100 == 0: print(f'Iteration {i}, loss: {loss.item()}') loss.backward() optimizer.step()Done! This was the implementation of a simple flow-based generative model in PyTorch from 0 to 100!
Acknowledgement
[1] Rezende and Mohamed 2015, Variational Inference with Normalizing Flows.
'*Generative Model > Generative Model' 카테고리의 다른 글
Understanding Generative Adversarial Networks (GANs) (0) 2024.05.05 How to Train Your Energy-Based Models (0) 2024.05.04 Two Formulations of Diffusion Models (0) 2024.04.29 Understanding Diffusion Probabilistic Models (DPMs) (0) 2024.04.27 [DDPM] Denoising Diffusion Probabilistic Models - Theory to Implementation (0) 2024.04.22