Self-Consistency Improves Chain of Thought Reasoning in Language Models

https://arxiv.org/pdf/2203.11171

---

Abstract

Chain-of-thought prompting combined with pre-trained large language models has achieved encouraging results on complex reasoning tasks. In this paper, we propose a new decoding strategy, self-consistency, to replace the naive greedy decoding used in chain-of-thought prompting. It first samples a diverse set of reasoning paths instead of only taking the greedy one, and then selects the most consistent answer by marginalizing out the sampled reasoning paths. Self-consistency leverages the intuition that a complex reasoning problem typically admits multiple different ways of thinking leading to its unique correct answer. Our extensive empirical evaluation shows that self-consistency boosts the performance of chain-of-thought prompting with a striking margin on a range of popular arithmetic and commonsense reasoning benchmarks, including GSM8K (+17.9%), SVAMP (+11.0%), AQuA (+12.2%), StrategyQA (+6.4%) and ARC-challenge (+3.9%).

---

1. Introduction

Although language models have demonstrated remarkable success across a range of NLP tasks, their ability to demonstrate reasoning is often seen as a limitation, which cannot be overcome solely by increasing model scale (Rae et al., 2021; BIG-bench collaboration, 2021, inter alia). In an effort to address this shortcoming, Wei et al. (2022) have proposed chain-of-thought prompting, where a language model is prompted to generate a series of short sentences that mimic the reasoning process a person might employ in solving a task. For example, given the question “If there are 3 cars in the parking lot and 2 more cars arrive, how many cars are in the parking lot?”, instead of directly responding with “5”, a language model would be prompted to respond with the entire chain-of-thought: “There are 3 cars in the parking lot already. 2 more arrive. Now there are 3 + 2 = 5 cars. The answer is 5.”. It has been observed that chain-of-thought prompting significantly improves model performance across a variety of multi-step reasoning tasks (Wei et al., 2022).

 

In this paper, we introduce a novel decoding strategy called self-consistency to replace the greedy decoding strategy used in chain-of-thought prompting (Wei et al., 2022), that further improves language models’ reasoning performance by a significant margin. Self-consistency leverages the intuition that complex reasoning tasks typically admit multiple reasoning paths that reach a correct answer (Stanovich & West, 2000). The more that deliberate thinking and analysis is required for a problem (Evans, 2010), the greater the diversity of reasoning paths that can recover the answer.

 

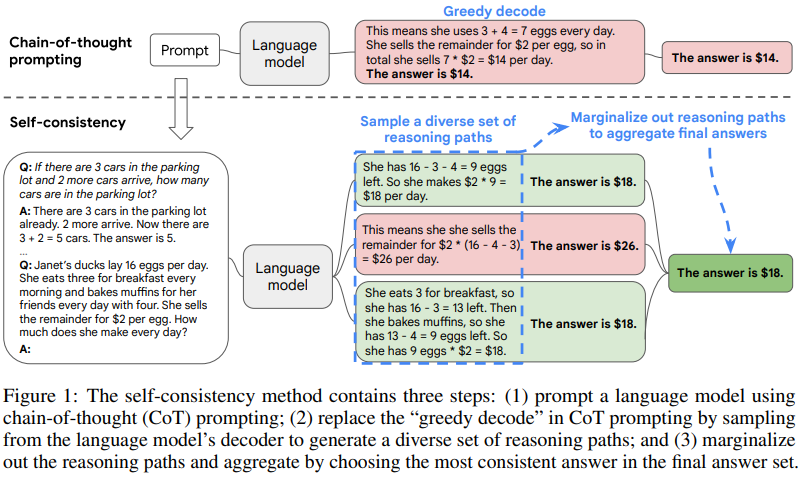
Figure 1 illustrates the self-consistency method with an example. We first prompt the language model with chain-of-thought prompting, then instead of greedily decoding the optimal reasoning path, we propose a “sample-and-marginalize” decoding procedure: we first sample from the language model’s decoder to generate a diverse set of reasoning paths; each reasoning path might lead to a different final answer, so we determine the optimal answer by marginalizing out the sampled reasoning paths to find the most consistent answer in the final answer set. Such an approach is analogous to the human experience that if multiple different ways of thinking lead to the same answer, one has greater confidence that the final answer is correct. Compared to other decoding methods, self-consistency avoids the repetitiveness and local-optimality that plague greedy decoding, while mitigating the stochasticity of a single sampled generation.

 

Self-consistency is far simpler than prior approaches that either train an additional verifier (Cobbe et al., 2021) or train a re-ranker given additional human annotations to improve generation quality (Thoppilan et al., 2022). Instead, self-consistency is entirely unsupervised, works off-the-shelf with pre-trained language models, requires no additional human annotation, and avoids any additional training, auxiliary models or fine-tuning. Self-consistency also differs from a typical ensemble approach where multiple models are trained and the outputs from each model are aggregated, it acts more like a “self-ensemble” that works on top of a single language model.

 

We evaluate self-consistency on a wide range of arithmetic and commonsense reasoning tasks over four language models with varying scales: the public UL2-20B (Tay et al., 2022) and GPT-3-175B (Brown et al., 2020), and two densely-activated decoder-only language models: LaMDA-137B (Thoppilan et al., 2022) and PaLM-540B (Chowdhery et al., 2022). On all four language models, self-consistency improves over chain-of-thought prompting by a striking margin across all tasks. In particular, when used with PaLM-540B or GPT-3, self-consistency achieves new state-of-the-art levels of performance across arithmetic reasoning tasks, including GSM8K (Cobbe et al., 2021) (+17.9% absolute accuracy gains), SVAMP (Patel et al., 2021) (+11.0%), AQuA (Ling et al., 2017) (+12.2%), and across commonsense reasoning tasks such as StrategyQA (Geva et al., 2021) (+6.4%) and ARCchallenge (Clark et al., 2018) (+3.9%). In additional experiments, we show self-consistency can robustly boost performance on NLP tasks where adding a chain-of-thought might hurt performance compared to standard prompting (Ye & Durrett, 2022). We also show self-consistency significantly outperforms sample-and-rank, beam search, ensemble-based approaches, and is robust to sampling strategies and imperfect prompts.

---

2. Self-Consistency over Diverse Reasoning Paths

A salient aspect of humanity is that people think differently. It is natural to suppose that in tasks requiring deliberate thinking, there are likely several ways to attack the problem. We propose that such a process can be simulated in language models via sampling from the language model’s decoder. For instance, as shown in Figure 1, a model can generate several plausible responses to a math question that all arrive at the same correct answer (Outputs 1 and 3). Since language models are not perfect reasoners, the model might also produce an incorrect reasoning path or make a mistake in one of the reasoning steps (e.g., in Output 2), but such solutions are less likely to arrive at the same answer. That is, we hypothesize that correct reasoning processes, even if they are diverse, tend to have greater agreement in their final answer than incorrect processes.

 

We leverage this intuition by proposing the following self-consistency method. First, a language model is prompted with a set of manually written chain-of-thought exemplars (Wei et al., 2022). Next, we sample a set of candidate outputs from the language model’s decoder, generating a diverse set of candidate reasoning paths. Self-consistency is compatible with most existing sampling algorithms, including temperature sampling (Ackley et al., 1985; Ficler & Goldberg, 2017), top-k sampling (Fan et al., 2018; Holtzman et al., 2018; Radford et al., 2019), and nucleus sampling (Holtzman et al., 2020). Finally, we aggregate the answers by marginalizing out the sampled reasoning paths and choosing the answer that is the most consistent among the generated answers.

 

In more detail, assume the generated answers ai are from a fixed answer set, ai ∈ A, where i = 1, . . . , m indexes the m candidate outputs sampled from the decoder. Given a prompt and a question, self-consistency introduces an additional latent variable ri, which is a sequence of tokens representing the reasoning path in the i-th output, then couples the generation of (ri , ai) where ri → ai, i.e., generating a reasoning path ri is optional and only used to reach the final answer ai . As an example, consider Output 3 from Figure 1: the first few sentences “She eats 3 for breakfast ... So she has 9 eggs * $2 = $18.” constitutes ri , while the answer 18 from the last sentence, “The answer is $18”, is parsed as ai. 1 After sampling multiple (ri , ai) from the model’s decoder, self-consistency applies a marginalization over ri by taking a majority vote over ai , i.e.,

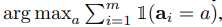
or as we defined as the most “consistent” answer among the final answer set.

 

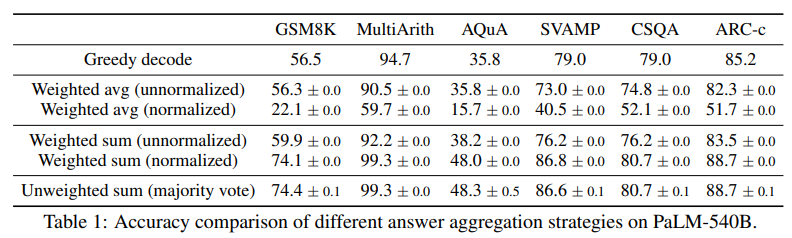
In Table 1, we show the test accuracy over a set of reasoning tasks by using different answer aggregation strategies. In addition to majority vote, one can also weight each (ri , ai) by P(ri , ai | prompt, question) when aggregating the answers. Note to compute P(ri , ai | prompt, question), we can either take the unnormalized probability of the model generating (ri , ai) given (prompt, question), or we can normalize the conditional probability by the output length (Brown et al., 2020), i.e.,

 

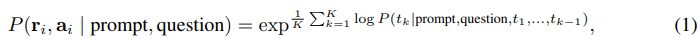
where log P(tk | prompt, question, t1, . . . , tk−1) is the log probability of generating the k-th token tk in (ri , ai) conditioned on the previous tokens, and K is the total number of tokens in (ri , ai). In Table 1, we show that taking the “unweighted sum”, i.e., taking a majority vote directly over ai yields a very similar accuracy as aggregating using the “normalized weighted sum”. We took a closer look at the model’s output probabilities and found this is because for each (ri , ai), the normalized conditional probabilities P(ri , ai | prompt, question) are quite close to each other, i.e., the language model regards those generations as “similarly likely”.2 Additionally, when aggregating the answers, the results in Table 1 show that the “normalized” weighted sum (i.e., Equation 1) yields a much higher accuracy compared to its unnormalized counterpart. For completeness, in Table 1 we also report the results by taking a “weighted average”, i.e., each a gets a score of its weighted sum divided by

which results in a much worse performance.

 

Self-consistency explores an interesting space between open-ended text generation and optimal text generation with a fixed answer. Reasoning tasks typically have fixed answers, which is why researchers have generally considered greedy decoding approaches (Radford et al., 2019; Wei et al., 2022; Chowdhery et al., 2022). However, we have found that even when the desired answer is fixed, introducing diversity in the reasoning processes can be highly beneficial; therefore we leverage sampling, as commonly used for open-ended text generation (Radford et al., 2019; Brown et al., 2020; Thoppilan et al., 2022), to achieve this goal. One should note that self-consistency can be applied only to problems where the final answer is from a fixed answer set, but in principle this approach can be extended to open-text generation problems if a good metric of consistency can be defined between multiple generations, e.g., whether two answers agree or contradict each other.

---

3. Experiments

We conducted a series of experiments to compare the proposed self-consistency method with existing approaches on a range of reasoning benchmarks. We find that self-consistency robustly improves reasoning accuracy for every language model considered, spanning a wide range of model scales.

---

3.1. Experiment Setup

Tasks and datasets.

We evaluate self-consistency on the following reasoning benchmarks.3

 

• Arithmetic reasoning. For these tasks, we used the Math Word Problem Repository (KoncelKedziorski et al., 2016), including AddSub (Hosseini et al., 2014), MultiArith (Roy & Roth, 2015), and ASDiv (Miao et al., 2020). We also included AQUA-RAT (Ling et al., 2017), a recently published benchmark of grade-school-math problems (GSM8K; Cobbe et al., 2021), and a challenge dataset over math word problems (SVAMP; Patel et al., 2021).

 

• Commonsense reasoning. For these tasks, we used CommonsenseQA (Talmor et al., 2019), StrategyQA (Geva et al., 2021), and the AI2 Reasoning Challenge (ARC) (Clark et al., 2018).

 

• Symbolic Reasoning. We evaluate two symbolic reasoning tasks: last letter concatenation (e.g., the input is “Elon Musk” and the output should be “nk”), and Coinflip (e.g., a coin is heads-up, after a few flips is the coin still heads-up?) from Wei et al. (2022).

 

Language models and prompts.

We evaluate self-consistency over four transformer-based language models with varying scales:

 

• UL2 (Tay et al., 2022) is an encoder-decoder model trained on a mixture of denoisers with 20- billion parameters. UL2 is completely open-sourced4 and has similar or better performance than GPT-3 on zero-shot SuperGLUE, with only 20B parameters and thus is more compute-friendly;

 

• GPT-3 (Brown et al., 2020) with 175-billion parameters. We use two public engines code-davinci001 and code-davinci-002 from the Codex series (Chen et al., 2021) to aid reproducibility;5

 

• LaMDA-137B (Thoppilan et al., 2022) is a dense left-to-right, decoder-only language model with 137-billion parameters, pre-trained on a mixture of web documents, dialog data and Wikipedia;

 

• PaLM-540B (Chowdhery et al., 2022) is a dense left-to-right, decoder-only language model with 540-billion parameters, pre-trained on a high quality corpus of 780 billion tokens with filtered webpages, books, Wikipedia, news articles, source code, and social media conversations.

 

We perform all experiments in the few-shot setting, without training or fine-tuning the language models. For a fair comparison we use the same prompts as in Wei et al. (2022): for all arithmetic reasoning tasks we use the same set of 8 manually written exemplars; for each commonsense reasoning task, 4-7 exemplars are randomly chosen from the training set with manually composed chain-of-thought prompts.6 Full details on the prompts used are given in Appendix A.3.

 

Sampling scheme.

To sample diverse reasoning paths, we followed similar settings to those suggested in Radford et al. (2019); Holtzman et al. (2020) for open-text generation. In particular, for UL2-20B and LaMDA-137B we applied temperature sampling with T = 0.5 and truncated at the top-k (k = 40) tokens with the highest probability, for PaLM-540B we applied T = 0.7, k = 40, and for GPT-3 we use T = 0.7 without top-k truncation. We provide an ablation study in Section 3.5 to show that self-consistency is generally robust to sampling strategies and parameters.

---

3.2. Main Results

We report the results of self-consistency averaged over 10 runs, where we sampled 40 outputs independently from the decoder in each run. The baseline we compare to is chain-of-thought prompting with greedy decoding (Wei et al., 2022), referred to as CoT-prompting, which has been previously used for decoding in large language models (Chowdhery et al., 2022).

 

Arithmetic Reasoning

The results are shown in Table 2. 7 Self-consistency improves the arithmetic reasoning performance over all four language models significantly over chain-of-thought prompting. More surprisingly, the gains become more significant when the language model’s scale increases, e.g., we see +3%-6% absolute accuracy improvement over UL2-20B but +9%-23% for LaMDA137B and GPT-3. For larger models that already achieve high accuracy on most tasks (e.g., GPT-3 and PaLM-540B), self-consistency still contributes significant additional gains with +12%-18% absolute accuracy on tasks like AQuA and GSM8K, and +7%-11% on SVAMP and ASDiv. With self-consistency, we achieve new state-of-the-art results on almost all tasks: despite the fact that self-consistency is unsupervised and task-agnostic, these results compare favorably to existing approaches that require task-specific training, or fine-tuning with thousands of examples (e.g., on GSM8K).

 

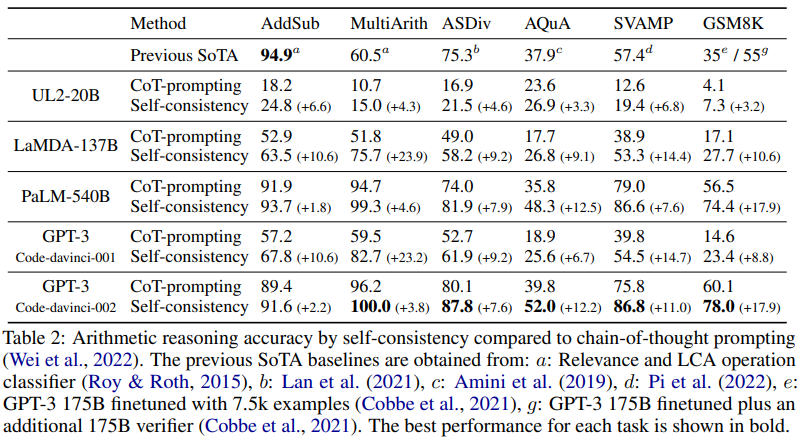
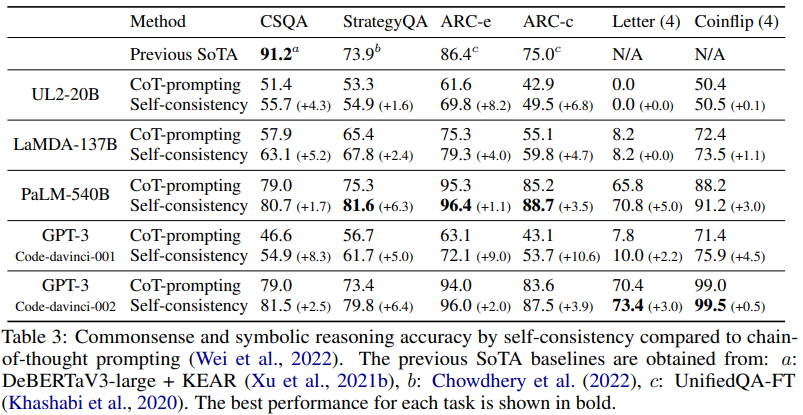
Commonsense and Symbolic Reasoning

Table 3 shows the results on commonsense and symbolic reasoning tasks. Similarly, self-consistency yields large gains across all four language models, and obtained SoTA results on 5 out of 6 tasks. For symbolic reasoning, we test the out-of-distribution (OOD) setting where the input prompt contains examples of 2-letters or 2-flips but we test examples of 4-letters and 4-flips (this setting is more challenging as PaLM-540B or GPT-3 can already achieve perfect in-distribution accuracy). In this challenging OOD setting, the gain of self-consistency is still quite significant compared to CoT-prompting with sufficient model sizes.

 

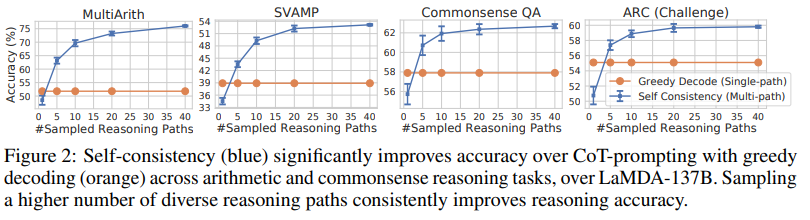
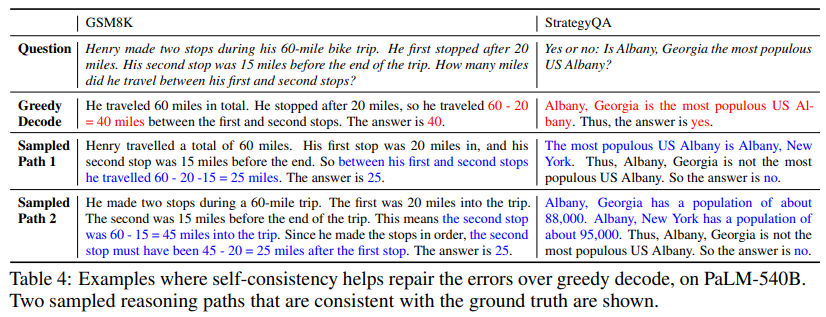
To show the effect of the number of sampled reasoning paths, we plot the accuracy (mean and standard deviation over 10 runs) with respect to varying numbers of sampled paths (1, 5, 10, 20, 40) in Figure 2. The results show that sampling a higher number (e.g., 40) of reasoning paths leads to a consistently better performance, further emphasizing the importance of introducing diversity in the reasoning paths. In Table 4, we show self-consistency yields a richer set of reasoning paths compared to greedy decoding with a few example questions from two tasks.

---

3.3. Self-Conistency Helps When Chain-of-Thought Hurts Performance

Ye & Durrett (2022) show that sometimes chain-of-thought prompting could hurt performance compared to standard prompting in few-shot in-context learning. Here we perform a study using self-consistency to see if it can help fill in the gap, over a set of common NLP tasks, including (1) Closed-Book Question Answering: BoolQ (Clark et al., 2019), HotpotQA (Yang et al., 2018), and (2) Natural Language Inference: e-SNLI (Camburu et al., 2018), ANLI (Nie et al., 2020) and RTE (Dagan et al., 2005; Bar-Haim et al., 2006; Giampiccolo et al., 2007; Bentivogli et al., 2009).

 

The results over PaLM-540B are shown in Table 5. For some tasks (e.g., ANLI-R1, e-SNLI, RTE), adding chain-of-thought does hurt performance compared to standard prompting (Brown et al., 2020), but self-consistency is able to robustly boost the performance and outperform standard prompting, making it a reliable way to add rationales in few-shot in-context learning for common NLP tasks.

---

3.4. Compare to Other Existing Approaches

We conduct a set of additional studies and show that self-consistency significantly outperforms existing methods including sample-and-rank, beam search, and ensemble-based approaches.

 

Comparison to Sample-and-Rank

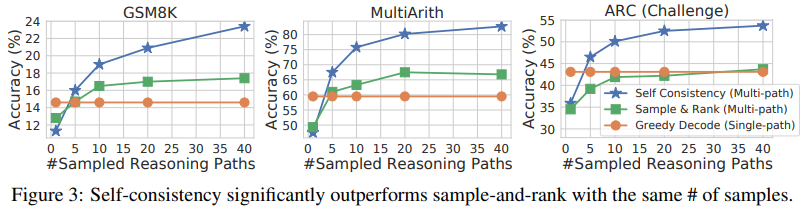
One commonly used approach to improve generation quality is sample-and-rank, where multiple sequences are sampled from the decoder and then ranked according to each sequence’s log probability (Adiwardana et al., 2020). We compare self-consistency with sample-and-rank on GPT-3 code-davinci-001, by sampling the same number of sequences from the decoder as self-consistency and taking the final answer from the top-ranked sequence. The results are shown in Figure 3. While sample-and-rank does improve the accuracy with additionally sampled sequences and ranking, the gain is much smaller compared to self-consistency.

 

Comparison to Beam Search

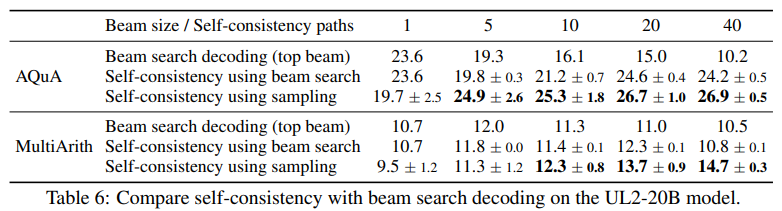
In Table 6, we compare self-consistency with beam search decoding on the UL2-20B model. For a fair comparison we report the accuracy under the same number of beams and reasoning paths. On both tasks self-consistency outperforms beam search significantly. Note self-consistency can also adopt beam search to decode each reasoning path (results are shown as “Self-consistency using beam search”), but its performance is worse compared to self-consistency with sampling. The reason is that beam search yields a lower diversity in the outputs (Li & Jurafsky, 2016), while in self-consistency the diversity of the reasoning paths is the key to a better performance.

 

Comparison to Ensemble-based Approaches

We further compare self-consistency to ensemble-based methods for few-shot learning. In particular, we consider ensembling by: (1) prompt order permutation: we randomly permute the exemplars in the prompt 40 times to mitigate model’s sensitivity to prompt order (Zhao et al., 2021; Lu et al., 2021); and (2) multiple sets of prompts (Gao et al., 2021): we manually write 3 different sets of prompts. We took majority vote of the answers from greedy decoding in both approaches as an ensemble. Table 7 shows that compared to self-consistency, existing ensemble-based approaches achieve a much smaller gain.8 In addition, note that self-consistency is different from a typical model-ensemble approach, where multiple models are trained and their outputs are aggregated. Self-consistency acts more like a “self-ensemble” on top of a single language model. We additionally show the results of ensembling multiple models in Appendix A.1.3 where the model-ensembles perform much worse compared to self-consistency.

---

3.5. Additional Studies

We conducted a number of additional experiments to analyze different aspects of the self-consistency method, including its robustness to sampling strategies and parameters, and how it works with imperfect prompts and non-natural-language reasoning paths.

 

Self-Consistency is Robust to Sampling Strategies and Scaling

We show self-consistency is robust to sampling strategies and parameters, by varying T in temperature sampling (Ackley et al., 1985; Ficler & Goldberg, 2017), k in top-k sampling (Fan et al., 2018; Holtzman et al., 2018; Radford et al., 2019), and p in nucleus sampling (Holtzman et al., 2020), over PaLM-540B in Figure 4 (left). Figure 4 (right) shows that self-consistency robustly improves performance across all scales for the LaMDA-137B model series. The gain is relatively lower for smaller models due to certain abilities (e.g., arithmetic) only emerge when the model reaches a sufficient scale (Brown et al., 2020).

 

Self-Consistency Improves Robustness to Imperfect Prompts

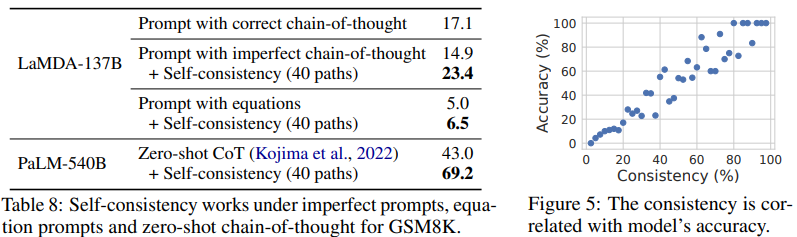
For few-shot learning with manually constructed prompts, human annotators sometimes make minor mistakes when creating the prompts. We further study if self-consistency can help improve a language model’s robustness to imperfect prompts.9 We show the results in Table 8: while imperfect prompts decrease accuracy with greedy decoding (17.1 → 14.9), self-consistency can fill in the gaps and robustly improve the results.

 

Additionally, we found that the consistency (in terms of % of decodes agreeing with the final aggregated answer) is highly correlated with accuracy (Figure 5, over GSM8K). This suggests that one can use self-consistency to provide an uncertainty estimate of the model in its generated solutions. In other words, one can use low consistency as an indicator that the model has low confidence; i.e., self-consistency confers some ability for the model to “know when it doesn’t know”.

 

Self-Consistency Works for Non-Natural-Language Reasoning Paths and Zero-shot CoT

We also tested the generality of the self-consistency concept to alternative forms of intermediate reasoning like equations (e.g., from “There are 3 cars in the parking lot already. 2 more arrive. Now there are 3 + 2 = 5 cars.” to “3 + 2 = 5”). The results are shown in Table 8 (“Prompt with equations”): self-consistency still improves accuracy by generating intermediate equations; however, compared to generating natural language reasoning paths, the gain is smaller since the equations are much shorter and less opportunity remains for generating diversity in the decoding process. In addition, we tested self-consistency with zero-shot chain-of-thought (Kojima et al., 2022) and show that self-consistency works for zero-shot CoT as well and improves the results significantly (+26.2%) in Table 8.

---

4. Related Work

Reasoning in language models.

Language models are known to struggle in Type 2 tasks, such as arithmetic, logical and commonsense reasoning (Evans, 2010). Previous work has primarily focused on specialized approaches for improving reasoning (Andor et al., 2019; Ran et al., 2019; Geva et al., 2020; Pi˛ekos et al., 2021). Compared to prior work, self-consistency is applicable to a wide range of reasoning tasks without any additional supervision or fine-tuning, while still substantially improving the performance of the chain-of-thought prompting approach proposed in Wei et al. (2022).

 

Sampling and re-ranking in language models.

Multiple decoding strategies for language models have been proposed in the literature, e.g., temperature sampling (Ackley et al., 1985; Ficler & Goldberg, 2017), top-k sampling (Fan et al., 2018; Holtzman et al., 2018; Radford et al., 2019), nucleus sampling (Holtzman et al., 2020), minimum Bayes risk decoding (Eikema & Aziz, 2020; Shi et al., 2022), and typical decoding (Meister et al., 2022). Other work has sought to explicitly promote diversity in the decoding process (Batra et al., 2012; Li et al., 2016; Vijayakumar et al., 2018).

 

Re-ranking is another common approach to improve generation quality in language models (Adiwardana et al., 2020; Shen et al., 2021). Thoppilan et al. (2022) collect additional human annotations to train a re-ranker for response filtering. Cobbe et al. (2021) train a “verifier” to re-rank generated solutions, which substantially improves the solve rate on math tasks compared to just fine-tuning the language model. Elazar et al. (2021) improve the consistency of factual knowledge extraction by extending pre-training with an additional consistency loss. All these methods require either training an additional re-ranker or collecting additional human annotation, while self-consistency requires no additional training, fine-tuning, nor extra data collection.

 

Extract reasoning paths.

Some previous work has considered task-specific approaches for identifying reasoning paths, such as constructing semantic graphs (Xu et al., 2021a), learning an RNN to retrieve reasoning paths over the Wikipedia graph (Asai et al., 2020), fine-tuning with human annotated reasoning paths on math problems (Cobbe et al., 2021), or training an extractor with heuristic-based pseudo reasoning paths (Chen et al., 2019). More recently, the importance of diversity in the reasoning processes has been noticed, but only leveraged via task-specific training, either through an additional QA model over extracted reasoning paths (Chen et al., 2019), or by the introduction of latent variables in a commonsense knowledge graph (Yu et al., 2022). Compared to these approaches, self-consistency is far simpler and requires no additional training. The approach we propose simply couples the generation of reasoning paths and a final answer by sampling from the decoder, using aggregation to recover the most consistent answer without additional modules.

 

Consistency in language models.

Some prior work has shown that language models can suffer from inconsistency in conversation (Adiwardana et al., 2020), explanation generation (Camburu et al., 2020), and factual knowledge extraction (Elazar et al., 2021). Welleck et al. (2020) use “consistency” to refer to generating an infinite-length sequence in recurrent language models. Nye et al. (2021) improve the logical consistency of samples from a System 1 model by adding a System 2-inspired logical reasoning module. In this paper we focus on a slightly different notion of “consistency”, i.e., utilizing answer consistency among diverse reasoning paths to improve accuracy.

---

5. Conclusion and Discussion

We introduced a simple yet effective method called self-consistency, and observed that it significantly improves accuracy in a range of arithmetic and commonsense reasoning tasks, across four large language models with varying scales. Beyond accuracy gains, self-consistency is also useful for collecting rationales when performing reasoning tasks with language models, and for providing uncertainty estimates and improved calibration of language model outputs.

 

One limitation of self-consistency is that it incurs more computation cost. In practice people can try a small number of paths (e.g., 5 or 10) as a starting point to realize most of the gains while not incurring too much cost, as in most cases the performance saturates quickly (Figure 2). As part of future work, one could use self-consistency to generate better supervised data to fine-tune the model, such that the model can give more accurate predictions in a single inference run after fine-tuning. In addition, we observed that language models can sometimes generate incorrect or nonsensical reasoning paths (e.g., the StrategyQA example in Table 4, the two population numbers are not exactly correct), and further work is needed to better ground models’ rationale generations.

---