[Lecture 12] (1/2) Deep Reinforcement Learning

https://storage.googleapis.com/deepmind-media/UCL%20x%20DeepMind%202021/Lecture%2012-%20Deep%20RL%201%20.pdf

https://www.youtube.com/watch?v=cVzvNZOBaJ4&list=PLqYmG7hTraZDVH599EItlEWsUOsJbAodm&index=12

---

Deep reinforcement learning is the combination of reinforcement learning algorithms with the use of deep neural networks as function approximators.

 

So the motivation for function approximation and the core ideas behind it is that, Tabular RL cannot possibly scale to certain large complex problems. The reason being that, if we want to estimate the value of each state separately for every single one state, this will have a memory cost that naively scales linearly with the state space which by itself would make it impractical. But even if we had unlimited memory, there was still a fundamental problem that it would be just very slow to learn the values of all states separately. So if we need to visit every single one and potentially multiple times to make an even reasonable guess of the value of the state, we are definitely in trouble. 

 

So a response is, the use of function approximation which is our key tool to generalize what we learn about one state to all other states that are close according to a reasonable definition of close. 

---

We have already introduced a function approximation, but the purpose of this chapter will be to discuss the use of deep neural networks specifically for the purpose of function approximation. 

 

And this is what is typically referred as Deep Reinforcement Learning. 

 

I will delve soon in some of the practical challenges that arise in this setting and some exciting research in the area. But before we go there, I want to take this introduction to recap a few core ideas of function apporximation in general and also to discuss the role of automatic differentiation in easily supporting anyone of you to freely experiment with deep reinforcement learning ideas. 

 

So when using function approximation to estimate values, we typically proposed a simple scheme where we would have some fixed mapping that transform any one state in some feature representation phi, and then we would have a parametric function that is linear and that maps features to values.

 

The problem of reinforcement learning then becomes to fit these parameters theta. So that's this value function v_theta makes predictions that are as close as possible to the true values v_pi for whatever policy pi we with to evaluate.

---

And we should have and we can turn this into concrete algorithms. So the first step would be to formalize the goal of minimizing the difference between v_theta and v_pi. So we could use as some loss function like the expected squarted error over the states. Typically this would also be weighted by the visitation distribution under the policy pi itself in order to allocate capacity sensibly.

 

And then given a loss function, we could use gradient ascent to optimize the loss function. 

 

This sounds very simple and easy, but doing this process for reinforcement learning introduces quite a few subtle challenges. 

---

First of all, computing the expectation over all states is too expensive, but this is maybe the least of the problem. The most deep problem is that, the vary target v_pi that we want to learn, to predict accurately is actually unknown. 

 

So the solution to both problems is, to sample the gradient descent update by considering just one or a few states in each update. And then use the sampled estimates of the v_pi as targets. 

 

And to do so, we can reuse all the idea that we have discussed, for instance, Model-free algorithms. 

 

So we can do Monte Carlo deep prediction by using an episodic return as target in the gradient update.

 

Or we could implement a deep TD prediction algorithm by bootstrapping on our own value estimates to construct the one step target, and again the bootstrap itself being parameterized by the very same parameters theta that we wish to update.

---

If some mapping phi is given, then it's possible to train a linear function to make reasonable value predictions. But today we want to consider a more complicated setting. So a setting where the feature mapping is too naive, and it's not informative enough to support reasonable value predictions if we have just a linear mapping on top of it.

 

And in this case, we might want to use a more complicated non-linear transformation from states to values, and for instance, by using a deep neural network as a function approximator. 

 

You may wonder why choosing a neural network. So it's valuable to stress that, these are by no means the only possible choice for a more complex function approximator. But neural networks do have some advantages. 

 

The first is that, this class of parametric function is well-known and is known to be able to discover quite effective feature representations that are tailored to any specific tasks that you might apply this parametric function to. So in our case, reinforcement learning, but the neural network have been used also for processing language or vision.

 

Importantly, this feature representation that is learned by a neural network is optimized in an end-to-end manner by the same gradient process that in linear function approximation is served just to define a linear mapping. So we have a unified way of training the entire parametric model to represent the states in a way that is expressive, and then make a reasonable value predictions from this representation.

 

The second reaons for to consider deep neural networks is that, given the extensive adption of deep learning methods in machine learning using neural networks allows us to leverage lots of great research. So all the ideas that have been introduced in supervised learning for network architectures or optimization, we can leverage all this grace research and benefit from it when we use neural networks for function approximation in reinforcement learning. 

---

What does parameterizing a value function with a neural network actually looks in practice? In the simplest case maybe, we could consider what is called the multi-layer perceptron. This would be a model that takes a very basic encoding of a state. So for instance, in a robot, this might be the raw sensor readings that we get and the MLP would then, take these as inputs, compute a hidden representation by applying a linear mapping, so W * S + b followed by a nonlinear transformation such as a tanh or a ReLU. And then, the actual value estimate would be computed as a linear function of this embedding.

 

But the important thing is that, this embedding would not be fixed, would be learned. And the parameters thetas are value estimates that then we train using deep RL would include not just the final linear mapping but also the parameters of the hidden representation. So the entire system would be trained end-to-end.

 

This sounds appealing but what if it to compute the gradient with respect to theta, we need to differentiate through not an MLP but a Convnet or what if we have a batch norm layer or we use a transformer. It turns out that, there is a way to compute exact derivatives on any of these architectures in a computationally efficient way that allows us to get any gradient we need without having to derive its expression ourselves. And given the popularity of deep learning in modern machine learning, these methods that are typically referred to as Autodiff are actuallly available in most scientific computing packages.

 

So in this chapter, we'll focusing mostly on the conceptual challenges of combining RL and deep learning and we'll mostly assume that we have these tools to support us in getting the gradients through any arbitrary neural network architecture that we may want to use for function approximation. 

 

But I want to give at least a brief intuition about how these tools work since they are so fundamental to everything that we do into the practice of deep RL. And specifically, I will give you a very brief introduction and also show you how you can use them to implement a very simple deep RL agent, specifically a Q-learning agent with a neural network as function approximation. 

---

The first important concept behind automatic differentiation is, the concept of the computational graph. So this is the abstract representation of any computation that you might want to perform, in our case, estimating a value, in the form of a direct acyclic graph. 

 

For instance, I show a very simple instance of such a computational graph where I have two inputs a and b, and I compute some intermediates representation as a+b, and b+1 respectively. This is a very simple example and then I compute some output by taking the product of these two numbers.

---

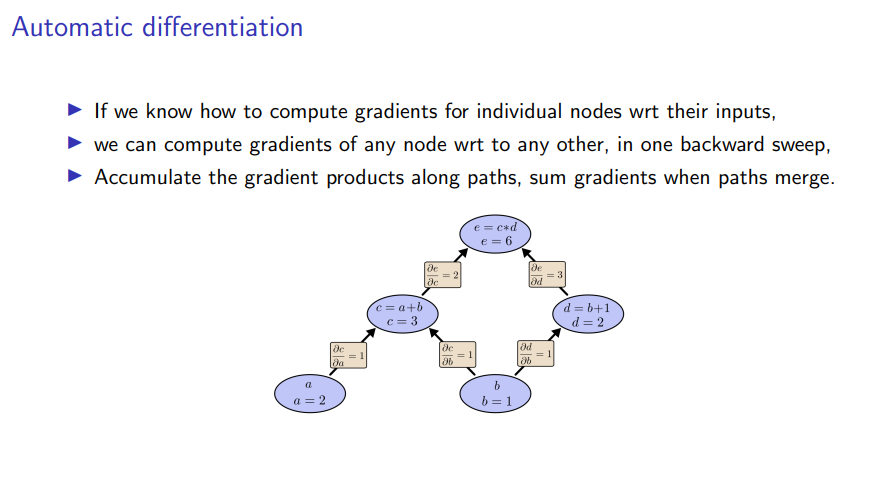
The reason computational graph are interesting to us is that, if we know how to compute gradients for individual nodes in a computational graph, we can automatically compute gradients for every node in the graph with respect to any other node in the graph. And do so, by just running the computation graph once forward from the inputs to all outputs and then, performing a single backward sweep through the graph, accumulating gradients along the path, and summing gradients when paths merge.

 

So for instance, the gradient of the output e with respect to input a can be computed by just taking the product of the derivative of e with respect to input c times the derivative of c with respect to input a, which is trivial compute, because you can always decompose your computation so that the individual nodes are really just simple arithmetic operations. 

 

If you take again in the simple example maybe a slightly more complicated derivative where we wanted the gradient of e with respect to the input b, then this will be just the sum of the derivative of e with respect to c times the derivative of c with respect to b, so this is one path from e to b. And then following the other path. We just need to take the gradient of e with respect to d and then times the derivative of d with respect to b and sum these two paths, since the two paths merge. 

 

This might even seem slightly magical at first but if you write it down, it's just implementing the standard chain rule. 

 

The advantage of doing this in the form of a computational graph is that, it helps implementing the chain rule, implement the gradient computation in an efficient way for any arbitrary numerical function by just decomposing your computation which in our case will be a program, decompose it into the sequence of basic operations, additions, multiplications and so on. And then, considering each of these basic operation in a node in the graph. That then we can differentiate by implementing the graph algorithm. 

 

I want to stress here that the entire process is not just computationally efficient. So it's always order of the cost of doing a forward bypass but it's also exact. So this is not a numerical approximation like you could do for instance by computing the gradients by infinite differences. This is an actual way of evaluating the true gradient of an arbitrary numerical function in a fully automatic way. It's really exciting if you think about it. 

---

---

To conclude the introduction, I want to show a very simple example of implementing a basic Q-learning agent that uses a neural network as a function approximator using an Autodiff tool from JAX. So what does such a deep Q-learning agent look like.

 

First, we will need to choose how to approximate Q-values and for this, we will use a single neural network. Let's say that takes the state input and outputs a vector output with one element for each available action. For instance, this network could be an MLP. Note that, this is we have implicitly made the design choice of the network taking a single state and outputting all action values. But this is not a strict requirement. We could also pass state and action both as inputs to the network, and then the network would return you just q value for detection. But in general, it tends to be more computational efficient if we can compute all q values in a single path. So this is a fairly common choice in pratice. 

---

---

Once we have a network, our job is not done if we want to implement deep Q-learning, we will also need to define a gradient update to the network parameters. And with Q-learning, this looks very much like the TD update. But we will be updating one specific action values. So the q_theta for specific S_t and A_t. 

 

And we will be using a target as a sample estimate of a return. The immediate reward plus the discounted max q value, where we're using our own estimates that depends on parameters thetas as a bootstrap. 

 

Often if you look for an implementation of a deep learning agent, you might see it written in a slightly different way for consistency with standard deep learning. You might see that, instead of defining directly a gradient update, they might define a pseudo-loss function which is the second equation that is, the one-half times the mean squared error between the chosen action and the target which is given by the rewards plus the discounted max q value. And this is fine but for this gradient of this loss function to actually recover the correct Q-learning updates, there are a couple of important caveats.

 

So first of all, when we compute the gradient of this loss, we need to ignore the dependency of max q on the parameters theta. This is denoted by the fact that we have a double vertical bar around max q, if we did not ignore this, then the gradient of this loss would not recover the first equation. We would have an additional term.

 

And the second is good to realize that, this is not a true loss function. It's a prop that has the property of returning you the right update when taking a gradient.

---

---

---