RoPE

https://www.slideshare.net/slideshow/roformer-enhanced-transformer-with-rotary-position-embedding/250482951

https://medium.com/ai-insights-cobet/rotary-positional-embeddings-a-detailed-look-and-comprehensive-understanding-4ff66a874d83

https://www.youtube.com/watch?v=o29P0Kpobz0

https://medium.com/@ngiengkianyew/understanding-rotary-positional-encoding-40635a4d078e

---

The Need for Positional Embeddings in Transformers

To understand the importance of RoPE, let’s first revisit why positional embeddings are crucial. Transformer models, by their inherent design, do not consider the order of input tokens.

 

For instance, phrases like “the dog chases the pig” and “the pig chases the dog,” though distinct in meaning, are treated indistinguishably as they are perceived as an unordered set of tokens. To maintain the sequence information and thus the meaning, positional embeddings are integrated into the model.

---

How Absolute Positional Embeddings Work

In the context of a sentence, suppose we have an embedding representing a word. To encode its position, we use another vector of identical dimensionality, where each vector uniquely represents a position in the sentence. For instance, a specific vector is designated for the second word in a sentence. Thus, each sentence position gets its distinct vector. The input for the Transformer layer is then formed by summing the word embedding with its corresponding positional embedding.

There are primarily two methods to generate these embeddings:

1. Learning from Data: Here, positional vectors are learned during training, just like other model parameters. We learn a unique vector for each position, say from 1 to 512. However, this introduces a limitation — the maximum sequence length is capped. If the model only learns up to position 512, it cannot represent sequences longer than that.

 

2. Sinusoidal Functions: This method involves constructing unique embeddings for each position using a sinusoidal function. Although the intricate details of this construction are complex, it essentially provides a unique positional embedding for every position in a sequence. Empirical studies have shown that learning from data and using sinusoidal functions offer comparable performance in real-world models.

Limitations of Absolute Positional Embeddings

Despite their widespread use, absolute positional embeddings are not without drawbacks:

 

1. Limited Sequence Length: As mentioned, if a model learns positional vectors up to a certain point, it cannot inherently represent positions beyond that limit.

 

2. Independence of Positional Embeddings: Each positional embedding is independent of others. This means that in the model’s view, the difference between positions 1 and 2 is the same as between positions 2 and 500. However, intuitively, positions 1 and 2 should be more closely related than position 500, which is significantly farther away. This lack of relative positioning can hinder the model’s ability to understand the nuances of language structure.

---

Understanding Relative Positional Embeddings

Rather than focusing on a token’s absolute position in a sentence, relative positional embeddings concentrate on the distances between pairs of tokens. This method doesn’t add a position vector to the word vector directly. Instead, it alters the attention mechanism to incorporate relative positional information.

Case Study: The T5 Model

One prominent model that utilizes relative positional embeddings is T5 (Text-to-Text Transfer Transformer). T5 introduces a nuanced way of handling positional information:

• Bias for Positional Offsets: T5 uses a bias, a floating-point number, to represent each possible positional offset. For example, a bias B1 might represent the relative distance between any two tokens that are one position apart, regardless of their absolute positions in the sentence.
• Integration in Self-Attention Layer: This matrix of relative position biases is added to the product of the query and key matrices in the self-attention layer. This ensures that tokens at the same relative distance are always represented by the same bias, regardless of their position in the sequence.
• Scalability: A significant advantage of this method is its scalability. It can extend to arbitrarily long sequences, a clear benefit over absolute positional embeddings.

Challenges with Relative Positional Embeddings

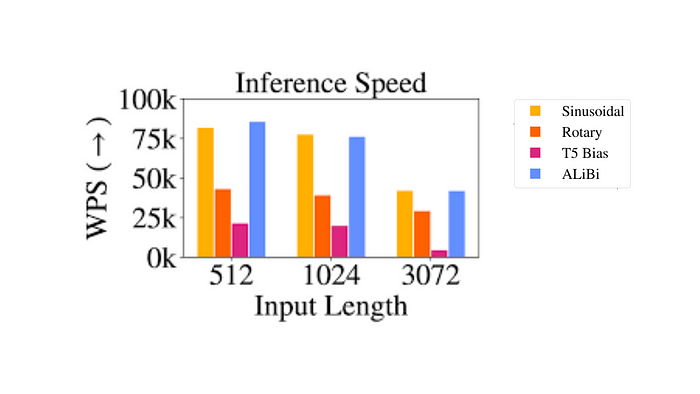
Despite their theoretical appeal, relative positional embeddings pose certain practical challenge.

1. Performance Issues: Benchmarks comparing T5’s relative embeddings with other types have shown that they can be slower, particularly for longer sequences. This is primarily due to the additional computational step in the self-attention layer, where the positional matrix is added to the query-key matrix.
2. Complexity in Key-Value Cache Usage: As each additional token alters the embedding for every other token, this complicates the effective use of key-value caches in Transformers. Key-value caches are crucial in enhancing efficiency and speed in Transformer models.

Due to these engineering complexities, relative embeddings haven’t been widely adopted, especially in larger language models.

---

What Are Rotary Positional Embeddings (RoPE)?

RoPE represents a novel approach in encoding positional information. Traditional methods, either absolute or relative, come with their limitations. Absolute positional embeddings assign a unique vector to each position, which though straightforward, doesn’t scale well and fails to capture relative positions effectively. Relative embeddings, on the other hand, focus on the distance between tokens, enhancing the model’s understanding of token relationships but complicating the model architecture.

 

RoPE ingeniously combines the strengths of both. It encodes positional information in a way that allows the model to understand both the absolute position of tokens and their relative distances. This is achieved through a rotational mechanism, where each position in the sequence is represented by a rotation in the embedding space. The elegance of RoPE lies in its simplicity and efficiency, enabling models to better grasp the nuances of language syntax and semantics.

The Mechanism of Rotary Positional Embeddings

 

RoPE introduces a novel concept. Instead of adding a positional vector, it applies a rotation to the word vector. Imagine a two-dimensional word vector for “dog.” To encode its position in a sentence, RoPE rotates this vector. The angle of rotation (θ) is proportional to the word’s position in the sentence. For instance, the vector is rotated by θ for the first position, 2θ for the second, and so on. This approach has several benefits:

1. Stability of Vectors: Adding tokens at the end of a sentence doesn’t affect the vectors for words at the beginning, facilitating efficient caching.
2. Preservation of Relative Positions: If two words, say “pig” and “dog,” maintain the same relative distance in different contexts, their vectors are rotated by the same amount. This ensures that the angle, and consequently the dot product between these vectors, remains constant

Matrix Formulation of RoPE

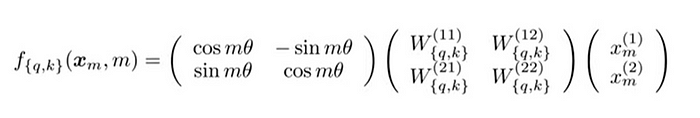
The technical implementation of RoPE involves rotation matrices. In a 2D case, the equation from the paper incorporates a rotation matrix that rotates a vector by an angle of Mθ, where M is the absolute position in the sentence. This rotation is applied to the query and key vectors in the self-attention mechanism of the Transformer.

 

For higher dimensions, the vector is split into 2D chunks, and each pair is rotated independently. This can be visualized as an n-dimensional corkscrew rotating in space.

 

Practically, this is implemented efficiently in libraries like PyTorch, requiring only about ten lines of code.

import torch
import torch.nn as nn

class RotaryPositionalEmbedding(nn.Module):
    def __init__(self, d_model, max_seq_len):
        super(RotaryPositionalEmbedding, self).__init__()

        # Create a rotation matrix.
        self.rotation_matrix = torch.zeros(d_model, d_model, device=torch.device("cuda"))
        for i in range(d_model):
            for j in range(d_model):
                self.rotation_matrix[i, j] = torch.cos(i * j * 0.01)

        # Create a positional embedding matrix.
        self.positional_embedding = torch.zeros(max_seq_len, d_model, device=torch.device("cuda"))
        for i in range(max_seq_len):
            for j in range(d_model):
                self.positional_embedding[i, j] = torch.cos(i * j * 0.01)

    def forward(self, x):
        """
        Args:
            x: A tensor of shape (batch_size, seq_len, d_model).

        Returns:
            A tensor of shape (batch_size, seq_len, d_model).
        """

        # Add the positional embedding to the input tensor.
        x += self.positional_embedding

        # Apply the rotation matrix to the input tensor.
        x = torch.matmul(x, self.rotation_matrix)

        return x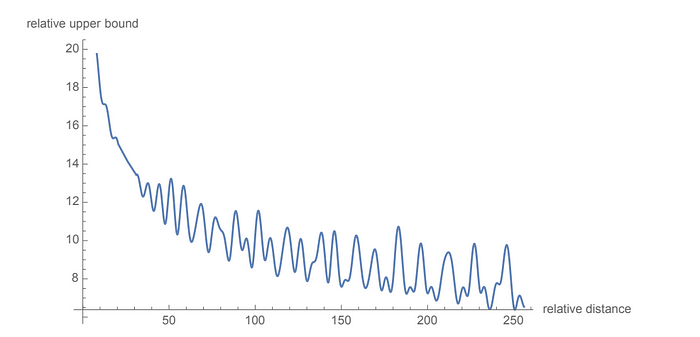

 

The rotation is executed through simple vector operations rather than matrix multiplication for efficiency. An important property is that words closer together are more likely to have a higher dot product, while those far apart have a lower one, reflecting their relative relevance in a given context.

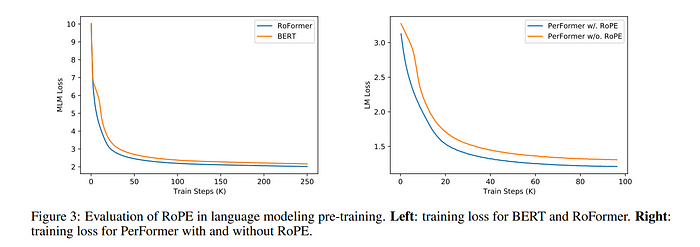
Experiments with models like RoBERTa and Performer, using RoPE, have shown faster training times compared to sinusoidal embeddings. This method has proven robust across various architectures and training setups.

 

In summary, Rotary Positional Embeddings represent a paradigm shift in Transformer architecture, offering a more robust, intuitive, and scalable way of encoding positional information. This advancement not only enhances current language models but also sets a foundation for future innovations in NLP. As we continue to unravel the complexities of language and AI, approaches like RoPE will be instrumental in building more advanced, accurate, and human-like language processing systems.

---

What is Rotary Positional Encoding

Rotary Positional Encoding is a type of position encoding that encodes absolute positional information with a rotation matrix and naturally incorporates explicit relative position dependency in self-attention formulation

What is a rotation matrix?

A rotation matrix is a matrix that rotates a vector to another vector by some angle.

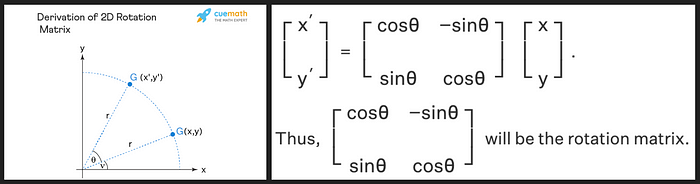
https://www.cuemath.com/algebra/rotation-matrix/

The rotation matrix preserves the magnitude (or length) of the original vector as indicated by ‘r’ in the image above, and the only thing that changes is the angle to the x-axis.

How is the 2-dimension Rotation Matrix involved in Rotary Positional Encoding?

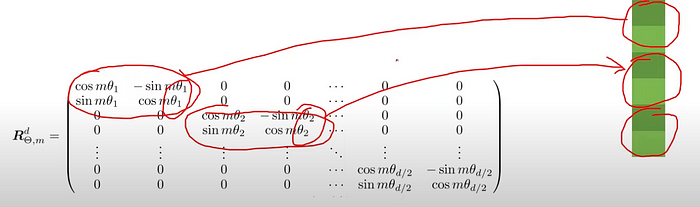
https://www.youtube.com/watch?v=o29P0Kpobz0&ab_channel=EfficientNLP

The Rotation Matrix used in Rotary Positional Encoding are multiple blocks of the 2-D rotation matrix!

---

 

This means that each word embedding is rotated by 3 pairs of rotation matrices, each with differing rotations that are affected by the positions of each word.

 

This means that positional encoding will take the word’s position into account, and we will now be able to generate different attention outputs for the same word in different positions

---

How does Rotary Positional Encoding overcome the disadvantages of Absolute and Relative Positional Encoding

Rotary Positional Encoding overcomes the disadvantages by combining the two.

Firstly let us see how it combines the two:

Absolute positional encoding in Rotary Positional Encoding

• Notice in our example for rotary positional encoding for ‘this’ and ‘is’, that the rotation matrix only depends on m * Thetha_i, where Thetha_i is shared across all the words, and m is just the position of the word (without a care as to what are the other positions of the other words)
• Similar to absolute positional encoding, we have one positional encoding for one position (without depending on other words’ position)

Relative Positional Encoding in Rotary Positional Encoding

• Since the angle of rotation depends on m * Thetha_i, words at the beginning of the sentence will have a smaller angle of rotation, and words at reaching the end of the sentence will have a larger angle of rotation, making the distances relative.
  → Remember: Thetha_i is the same for all the words, m the position of the word is the only thing that changes. Higher m means m * Thetha_i, which means a larger angle of rotation.
• Similar to relative positional encoding, there is a relationship between the positional encodings of different positions

Now, to explain why it overcomes the disadvantages, let us review the disadvantages of both methods:

• Absolute Positional Encoding: (1) Does not include relative positional information
• Relative Positional Encoding: (2) Computationally inefficient, (3) Not suitable for inference

Therefore we know that Rotary Positional Encoding must have the following properties:

1. Includes relative positional information
2. Be Computationally efficient
3. Be suitable for inference

(Property 1) Rotary Positional Encoding includes relative positional information

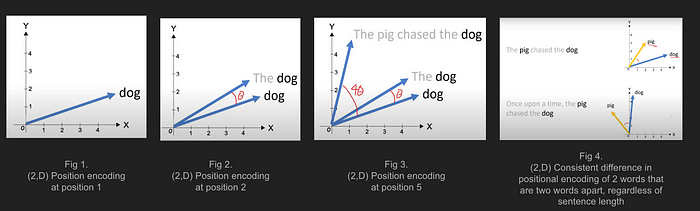
https://www.youtube.com/watch?v=o29P0Kpobz0&ab_channel=EfficientNLP

• Rotary Positional Encoding includes relative positional information by making the angles in the rotation matrix dependent on the current word’s position, and by properties of the rotation matrix, tell us how far apart two words are.
• For example in Fig 4. above, the angle between ‘pig’ and ‘dog’ is the same even though they (1) appear in 2 sentences that are of different lengths, and (2) ‘pig’ and ‘dog’ appear in different positions of the sentence!
  → (if you calculate the dot product between ‘pig’ and ‘dog’ in both sentences, they will be the same)
  → Angle is the same the words ‘pig’ and ‘dog’ are always 2 words apart (with ‘chased the’ between ‘pig’ and ‘dog’).
  → Remember that the angle of rotation of a word is m * Thetha_i, and the angle between the ‘pig’ and ‘dog’ that are 2 words apart is (m_{dog}-m_{pig}= 2 * Thetha_i

Another way to look at it is by charting the angle inside the rotation matrix for different positions:

 

1. Remember that the angle inside the rotation matrix is indicated by: m * Theta_i

→ The y-axis represents the angle of rotation
→ The x-axis represents the hidden dimension

 

For the chart below, you should look at the upward shift of the entire graph to investigate the impact of changing m (the position of the word)

Graph for angles inside the rotation matrix for different positions from pos-1 to pos-7

2. From the graph, we can see a consistent pattern when t increases from 1 to 7, the angle of rotation increases as well (as indicated by the shift of the entire graph). This means that if the positional encoding of a word has a larger angle of rotation, the word is further along the sentence.
→ The gap between t=1 and t=3 is larger than the gap between t=1 and t=2

 

3. From the graph, we note that the magnitude of differences between two consecutive pairs of position is the same.
→ This means that the change in one time step brought about relatively the same change in angle of rotation. For example, gaps between t=1 and t=2 is the same as t=2 and t=3, so on and so forth.
→ This means that the relative distances are consistent. For example, Any two words that are 3 words apart will have the same angle of rotation.

(Another perspective for Property1)

1. Thus far we talked only about the “angle of rotation”, but where is the part that encodes the relative distances from one word to other positions?. The answer lies in the following definition of dot product:
→ “The dot product of vectors A and B is equal to the length of A times the length of B times the cosine of the angle between them A · B = |A||B| cos(θ)”

 

2. If we do the dot product between the rotary position encoding of position 1 and the other positions, we get back cos(θ) which only depends on the angle of the rotation (more explicitly the difference in the angle of rotation from position 1 to the other word’s position).

 

3. The angle of rotation for position = 1 is less than angles of rotations for positions > 1. This means that the further away the other word is from position 1, (1) the larger the difference in the angle of rotation (2) the smaller the dot product (because the value of cosine drops from 0 to π) (3) the further away the other word is from position 1

 

4. We conclude that rotary positional encoding includes relative positional information

 

How to use Rotary Positional Encoding:
- Because we need the dot product to include relative positional encoding, we apply rotary positional encoding to Query and Key separately, so that when we matrix multiply them together, the attention matrix contains the relative positional information. (refer to this repo)

(Property 2) Rotary Positional Encoding is computationally efficient

• It may seem like using Rotary Positional Encoding is not computationally efficient because we have to create the rotation matrix, but the researchers have found a computationally efficient formula.

Rotary Positional Embeddings (RoPE)

(Property 3) Rotary Positional Encoding is suitable for inference

• Since we already know that Rotary Positional Encoding is like absolute positional encoding in that the encodings depend only on the current word position, the positional encodings for words that had already been generated do not change, making KV cache possible again during inference

---

Conclusion

• The disadvantage of absolute positional encoding is that it does not take into account the relative positional information in a sentence
• The disadvantage of relative positional encoding is that it is computationally expensive and not suitable for inference
• Rotary Positional Encoding combines the two by taking advantage of each method and also makes use of a computationally efficient way to compute it efficiently
• Rotary Positional Encoding’s foundational idea is to make use of D//2 two-dimensional rotation matrix to rotate a D-dimensional matrix, where each two-dimensional rotation matrix’s angle of rotation is determined by m * Thetha (where m is the position of the word, and Theta, is a precomputed term that is shared across all the words), and produces an exponential looking curve. When m increases, the exponential-looking curve shifts upwards to a larger value to indicate a higher positional distance