-
[Lag-Llama] Towards Foundation Models for Probabilistic Time Series Forecasting*Paper Writing 1/Related_Work 2024. 10. 18. 22:02
https://arxiv.org/pdf/2310.08278
https://github.com/time-series-foundation-models/lag-llama
(Oct 2023)
Abstract
Over the past years, foundation models have caused a paradigm shift in machine learning due to their unprecedented capabilities for zero-shot and few-shot generalization. However, despite the success of foundation models in modalities such as natural language processing and computer vision, the development of foundation models for time series forecasting has lagged behind. We present Lag-Llama, a general-purpose foundation model for univariate probabilistic time series forecasting based on a decoder-only transformer architecture that uses lags as covariates. Lag-Llama is pretrained on a large corpus of diverse time series data from several domains, and demonstrates strong zero-shot generalization capabilities compared to a wide range of forecasting models on downstream datasets across domains. Moreover, when fine-tuned on relatively small fractions of such previously unseen datasets, Lag-Llama achieves state-of-the-art performance, outperforming prior deep learning approaches, emerging as the best general-purpose model on average. Lag-Llama serves as a strong contender to the current state-of-art in time series forecasting and paves the way for future advancements in foundation models tailored to time series data.
1. Introduction
Probabilistic time series forecasting is an important practical problem arising in a wide range of applications, from finance and weather forecasting to brain imaging and computer systems performance management (Peterson, 2017). Accurate probabilistic forecasting is usually an essential step towards the subsequent decision-making in such practical domains. The probabilistic nature of such forecasting endows decision-makers with a notion of uncertainty, allowing them to consider a variety of future scenarios, along with their respective likelihoods. Various methods have been proposed for this task, ranging from classical autoregressive models (Hyndman & Athanasopoulos, 2021) to the more recent neural forecasting methods based on deep learning architectures (Torres et al., 2021). Note that the overwhelming majority of these previous approaches are focused on building dataset-specific models, i.e. models tested on the same dataset in which training is performed.
Recently, however, machine learning is witnessing a paradigm shift due to the rise of foundation models (Bommasani et al., 2022) — large-scale, general-purpose neural networks pretrained in an unsupervised manner on large amounts of diverse data across various data distributions. Such models demonstrate remarkable few-shot generalization capabilities on a wide range of downstream datasets (Brown et al., 2020a), often outperforming dataset-specific models. Following the successes of foundation models in language and image processing domains(OpenAI, 2023; Radford et al., 2021), we aim to develop foundation models for time series, investigate their behaviour at scale, and push the limits of transfer achievable across diverse time series domains.
In this paper, we present Lag-Llama— a foundation model for probabilistic time series forecasting trained on a large collection of open time series data, and evaluated on unseen time series datasets. We investigate the performance of Lag-Llama across several settings where unseen time series datasets are encountered downstream with different levels of data history being available, and show that Lag-Llama performs comparably or better against state-of-the-art dataset-specific models.
Our contributions:
• We present Lag-Llama, a foundation model for univariate probabilistic time series forecasting based on a simple decoder-only transformer architecture that uses lags as covariates.
• We show that Lag-Llama, when pretrained from scratch on a broad, diverse corpus of datasets, has strong zero-shot performance on unseen datasets, and performs comparably to models trained on the specific datasets.
• Lag-Llama also demonstrates state-of-the-art performance across diverse datasets from different domains after finetuning, and emerges as the best general-purpose model without any knowledge of downstream datasets.
• We demonstrate the strong few-shot adaptation performance of Lag-Llama on previously unseen datasets, across varying fractions of data history being available.
• We investigate the diversity of the pretraining corpus used to train Lag-Llama, and present the scaling laws of Lag-Llama with respect to the pretraining data.
2. Related Work
Statistical models
have been the cornerstone of time series forecasting for decades, evolving continuously to address complex forecasting challenges. Traditional models such as ARIMA (Autoregressive Integrated Moving Average) set the foundation by using autocorrelation to forecast future values. ETS (Error, Trend, Seasonality) models advanced this by decomposing a time series into its fundamental components, allowing for more nuanced forecasting that captures trends and seasonal patterns. Theta models, introduced by Assimakopoulos & Nikolopoulos (2000), represented another significant advancement in time series forecasting. By applying a decomposition technique combining both long-term trend and seasonality, these models offer a simple yet effective method for forecasting Despite the success of the considerable successes of these statistical models and more advanced ones (Croston, 1972; Syntetos & Boylan, 2005; Hyndman & Athanasopoulos, 2018), these models share common limitations. Their primary shortfall lies in their inherent assumption of linear relationships and stationarity in time series data, which is often not the case in real-world scenarios marked by abrupt changes and non-linear dynamics. Furthermore, they may require extensive manual tuning and domain knowledge to select appropriate models and parameters for specific forecasting tasks.
Neural forecasting
is a rapidly developing research area following the explosion of machine learning (Benidis et al., 2022). Various architectures have been developed for this setting, starting with RNN-based and LSTM-based models (Salinas et al., 2020; Wen et al., 2018). More recently in light of the recent success of transformers (Vaswani et al., 2017) for sequence-to-sequence modelling for natural language processing, many variations of transformers have been proposed for time series forecasting. Different models (Nie et al., 2023a; Wu et al., 2020a;b) process the input time series in different ways to be digestible by a vanilla transformer, then re-process the output of a transformer for a point forecast or a probabilistic forecast. On the other hand, various other works propose alternative strategies to vanilla attention and build off the transformer architecture, for better models tailored for time series (Lim et al., 2021; Li et al., 2023; Ashok et al., 2023; Oreshkin et al., 2020a; Zhou et al., 2021a; Wu et al., 2021; Woo et al., 2023; Liu et al., 2022b; Zhou et al., 2022; Liu et al., 2022a; Ni et al., 2023; Li et al., 2019; Gulati et al., 2020).
Foundation models
are an emerging paradigm of self-supervised (or) unsupervised learning on large datasets (Bommasani et al., 2022). Many such models (Devlin et al., 2019; OpenAI, 2023; Chowdhery et al., 2022; Radford et al., 2021; Wang et al., 2022) have demonstrated adaptability across modalities, extending beyond web data to scientific domains such as protein design (Robert Verkuil, 2022). Scaling the model, dataset size and data diversity have also been shown to result in remarkable transfer capabilities and excellent few-shot learning on novel datasets and tasks (Thrun & Pratt, 1998; Brown et al., 2020b). Self-supervised learning techniques have also been proposed for time series (Li et al., 2023; Woo et al., 2022a; Yeh et al., 2023). Most related to our work is Yeh et al. (2023) who train on a corpus of time series datasets. The key difference is that they validate their model only on the downstream classification tasks, and do not validate on forecasting tasks. Works such as Time-LLM (Jin et al., 2023), LLM4TS (Chang et al., 2023), GPT2(6) (Zhou et al., 2023a), UniTime (Liu et al., 2023), and TEMPO (Anonymous, 2024) freeze LLM encoder backbones while simultaneously fine-tuning/adapting the input and distribution heads for forecasting. The main goal of our work is to apply the foundation model approach to time series data and to investigate the extent of the transfer achievable across a wide range of time series domains.
3. Probabilistic Time Series Forecasting


4. Lag-Llama
We present Lag-Llama, a foundation model for univariate probabilistic forecasting. The first step in building such a foundation model for time series is training on a large corpus of diverse time series. When training on heterogenous univariate time series corpora, the frequency of the time series in our corpus varies. Further, when adapting our foundation model to downstream datasets, we may encounter new frequencies and combinations of seen frequencies, which our model should be capable of handling. We now present a general method for tokenizing series from such a dataset, without directly relying on the frequency of any specific dataset, and thus potentially allowing unseen frequencies and combinations of seen frequencies to be used at test time.
4.1. Tokenization: Lag Features
The tokenization scheme of Lag-Llama involves constructing lagged features from the prior values of the time series, constructed according to a specified set of appropriate lag indices that include quarterly, monthly, weekly, daily, hourly, and second-level frequencies. Given a sorted set of positive lag indices L = {1, . . . , L}*, we define the lag operation on a particular time value as xt |→ kt ∈ R |L| where each entry j of kt is given by kt[j] = xt−L[j] . Thus to create lag features for some context-length window x1:C we need to sample a larger window with L more historical points denoted by x−L:C ¶ . In addition to these lagged features, we add date-time features of all the frequencies in our corpus, namely second-of-minute, hour-of-day, etc. up till the quarter-of-year from the time index t. Note that while the primary goal of these date-time features is to provide additional information, for any time series, all except one date-time feature will remain constant from one time-step to the next, and from the model can implicitly make sense of the frequency of the time series as well. Assuming we employ a total of F date-time features, each of our tokens is of size |L| + F. Fig. 1 shows an example tokenization. We note that a downside to using lagged features in tokenization is that it requires an L-sized or larger context window.

4.2. Lag-Llama Architecture
Lag-Llama’s architecture is based on the decoder-only transformer-based architecture LLaMA (Touvron et al., 2023).
Fig. 2 shows a general schematic of this model with M decoder layers. A univariate sequence of length x i −L:C along with its covariates is tokenized by concatenating the covariate vectors to a sequence of C tokens x i 1:C . These tokens are passed through a shared linear projection layer that maps the features to the hidden dimension of the attention module. Similar to in Touvron et al. (2023), Lag-Llama incorporates pre-normalization via the RMSNorm (Zhang & Sennrich, 2019) and Rotary Positional Encoding (RoPE) (Su et al., 2021) at each attention layer’s query and key representations as in LLaMA (Touvron et al., 2023).
After passing through the causally masked transformer layers, the model predicts the parameters ϕ of the forecast distribution of the next timestep, where the parameters are output by a parametric distribution head, as described in Sec. 4.3. The negative log-likelihood of the predicted distribution of all predicted timesteps is minimized.
At inference time, given a time series of size at least L, we can construct a feature vector that is passed to the model to obtain the distribution of the next time point. In this fashion, via greedy autoregressive decoding, we can obtain many simulated trajectories of the future up to our chosen prediction horizon P ≥ 1. From these empirical samples, we can calculate the uncertainty intervals for downstream decision-making tasks and metrics with respect to held-out data.

4.3. Choice of Distribution Head
The last layer of Lag-Llama is a distinct layer known as the distribution head, which projects the model’s features to the parameters of a probability distribution. We can combine different distribution heads with the representational capacity of the model to output the parameters ϕ of any parametric probability distribution. For our experiments, we adopt a Student’s t-distribution (Student, 1908) and output the three parameters corresponding to this distribution, namely its degrees of freedom, mean, and scale, with appropriate nonlinearities to ensure the appropriate parameters stay positive. More expressive choices of distributions, such as normalizing flows (Rasul et al., 2021b) and copulas (Salinas et al., 2019a; Drouin et al., 2022; Ashok et al., 2023) are potential choices of distribution heads, however with the potential overhead of difficulties in model training and optimization. The goal of our work was to keep the model as simple as possible, which led us to adopt a simple parametric distributional head. We leave the exploration of such distribution heads for future work.
4.4. Value Scaling
When training on a large corpus of time series data from different datasets and domains, each time series can be of different numerical magnitude. Since we pretrain a foundation model over such data, we utilize the scaling heuristic (Salinas et al., 2019b) where for each univariate window, we calculate its mean value µ i = summation C t=1 x i t / C and variance σ i . We can then replace the time series x i 1:C in the window by {(x i t − µ i )/σi} C t=1. We also incorporate µ i and σ i as time independent real-valued covariates for each token, to give the model information of the statistics of the inputs, which we call summary statistics.
During training and obtaining likelihood, the values are transformed using the mean and variance, while sampling, every timestep of data that is sampled is de-standardized using the same mean and variance. In practice, instead of the standard scaler, we find the following standardization strategy works well when pretraining our model.
Robust Standardization
ensures that our time series processing is robust to outliers. This procedures normalizes the series by removing the median and scaling according to the Interquartile Range (IQR) (Dekking et al., 2005). For a context-window sized series x1:C = {x1, x2, ..., xC } we standardize each time point as:
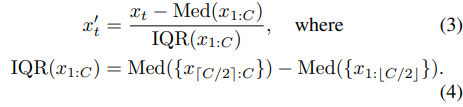
4.5. Training Strategies
We employ a series of training strategies to effectively pretrain Lag-Llama on the corpus of datasets. Firstly, we find that employing a stratified sampling approach where the datasets in the corpus are weighed by the amount of total number of series is useful when sampling random windows from the pretraining corpus. Further, we find that employing time series augmentation techniques of Freq-Mix and Freq-Mask (Chen et al., 2023) serve useful to reduce overfitting. We search the hyperparameters of these augmentation strategies as part of our hyperparameter search.
5. Experimental Setup
5.1. Datasets
We collate a diverse corpus of 27 time series datasets from several sources across six different semantically grouped domains such as energy, transportation, economics, nature, air quality and cloud operations; each dataset has a different set of characteristics, such as prediction lengths, number of series, lengths of each series, and frequencies.
We leave out a few datasets from each domain for testing the few-shot generalization abilities of the pretrained model, whle using the remaining datasets for pretraining the foundation model. Furthermore, we set aside datasets from entirely different domains to assess our model’s performance on data that may lack any potential similarity to the datasets in pretraining. Such a setup mimics the real-world use of our model, where one may adapt it for datasets that fall closely within the distribution of domains that the model has been trained on, as well as datasets in completely different domains. Our pretraining corpus comprises a total of 7, 965 different univariate time series, each of different lengths, when put together, comprising a total of around 352 million data windows (tokens) for our model to train on. App. §A lists the datasets we use, along with their sources and properties, their respective domains, and the dataset split used in our experiments.
Note that the term “domain” used here is just a label used to group several datasets, which does not represent a common source or data distribution; each of the pretraining and test datasets possesses very different general characteristics (patterns, seasonalities), apart from having other distinct properties. We use the default prediction length of each dataset for evaluation and ensure that there is a wide variety of prediction horizons in our unseen corpus of datasets, to evaluate models on short-term, medium-term, and long-term forecasting setups. App. §A lists the different datasets used in this work, along with the sources and properties of each dataset. Sec. § 7.1 analyses the diversity of our corpus of datasets.
5.2. Baselines
We compare the performance of Lag-Llama to that of a large set of baselines, including both standard statistical models, as well as deep neural networks.
Through AutoGluon (Shchur et al., 2023), an AutoML framework for probabilistic time series forecasting, we benchmark against 5 well-known statistical time series forecasting models: AutoARIMA (Hyndman & Khandakar, 2008) and AutoETS (Hyndman & Khandakar, 2008) which are established statistical models that tune model parameters locally for each time series (Hyndman & Khandakar, 2008), CrostonSBA (Syntetos and Boylan Approximate) (Croston, 1972; Syntetos & Boylan, 2005) an intermittent demand forecasting model using Croston’s model with the Syntetos-Boylan bias correction approach, DynOptTheta (The Dynamically Optimized Theta model) (Box & Jenkins, 1976) a statistical forecasting method that is based on the decomposition of the time series into trend, seasonality and noise, and NPTS (Non-Parametric Time Series Forecaster) (Shchur et al., 2023), a local forecasting method that assumes a non-parametric sampling distribution. We further compare with 3 strong deep-learning methods through the same AutoGluon framework: DeepAR (Salinas et al., 2020), an autoregressive RNN-based method that has been shown to be a strong contender for probabilistic forecasting (Alexandrov et al., 2020), PatchTST (Nie et al., 2023b) a univariate transformer-based method that uses patching to tokenize time series, TFT (Temporal Fusion Transformer) (Lim et al., 2021), an attention-based architecture with recurrent and feature-selection layers.
We benchmark against 4 more deep learning models: NBEATS (Oreshkin et al., 2020b), a neural network architecture that uses a recursive decomposition based on projecting residual signals on learned basis functions, Informer (Zhou et al., 2021c), an efficient autoregressive transformerbased method that uses a ProbSparse self-attention mechanism to handle extremely long sequences, AutoFormer (Wu et al., 2022), a transformer-based architecture with an AutoCorrelation mechanism based on the series periodicity, and ETSFormer (Woo et al., 2022b), a transformer that replaces self-attention with exponential smoothing attention and frequency attention. We finally benchmark against OneFitsAll (Zhou et al., 2023b), a method that leverages a pretrained large language model (LLM) (GPT-2 (Radford et al., 2019)) and finetunes the input and output layers for time series forecasting.
Note that all the methods are compared in the univariate setup, where, similar to Lag-Llama, each time series is treated and forecasted independently. All methods produced using AutoGluon support probabilistic forecasts. All the other models (N-BEATS, Informer, AutoFormer, ETSFormer, and OneFitsAll) were originally designed for point forecasting and clean normalized data; we adapt them for probabilistic forecasting by using a distribution head at the output and endowing them with all the features similar to Lag-Llama such as value scaling.

5.3. Hyperparameter Search and Model Training Setups
We perform a random search of 100 different hyperparameter configurations and use the validation loss of the pretraining corpus to select our model. We elaborate on our hyperparameter search and model selection in Appendix D. During pretraining, we use the batch size of 256 and a learning rate of 10−4 . Each epoch consists of 100 randomly sampled windows, each of length L+C as described in Sec. 4.1. We use an early stopping criterion of 50 epochs based on the average validation loss of the training datasets in our pretraining corpus. When fine-tuning for a specific dataset, we train our models with the same batch size and learning rate, and each epoch consists of 100 randomly sampled windows from the specific dataset, each of length L + (C + P), where P now is the prediction length of the specific dataset. Since our model is decoder-only, and since prediction length is not fixed, the model can therefore work for any downstream prediction length. We use an early stopping criterion of 50 epochs during fine-tuning, based on the validation loss of the dataset being finetuned on. We elaborate on our training procedure in Appendix B. For all the models trained in this paper, we use a single Nvidia Tesla-P100 GPU with 12 GB of memory, 4 CPU cores, and 24 GB of RAM.
5.4. Inference and Model Evaluation
Inference for a specific dataset is performed by sampling from the Lag-Llama model autoregressively, starting with conditioning on the context of length C, until a prediction length P, which is defined for a given dataset. We use the Continuous Ranked Probability Score (CRPS) (Gneiting & Raftery, 2007; Matheson & Winkler, 1976), a common metric in the probabilistic forecasting literature (Rasul et al., 2021b;a; Salinas et al., 2019a; Shchur et al., 2023), for evaluating our model’s performance. We use 100 empirical samples and report the CRPS averaged over the prediction horizon and across all the time series of a dataset. We further assess how well each method we benchmark on does as a general-purpose forecasting algorithm, rather than a dataset-specific one, by measuring the average rank of each method, with respect to all others, over all the datasets.
6. Results
We first evaluate zero-shot performance of our pretrained Lag-Llama on the unseen datasets (subsection 6.1), when no samples from the new downstream domain are available for possible fine-tuning of the the model. Note that such zero-shot forecasting scenarios are common in time series forecasting literature (see, for example, the cold-start problem (Wikipedia, 2024; Fatemi et al., 2023)). We then fine-tune our pretrained Lag-Llama on each unseen dataset and evaluate the model after fine-tuning, to study how our pretrained model adapts to different unseen datasets and domains when there is considerable history available in the dataset to train on. We then evaluate the few-shot adaptation performance of our foundation model — a well-known scenario in other modalities (e.g., text) where foundation models are expected to demonstrate strong generalization capabilities. We vary the amount of history available for fine-tuning on each dataset, and present the few-shot adaptation performance of our model at various levels of history.

6.1. Zero-Shot & Finetuing Performance on New Data
Tab. 1 presents the results comparing the performance of supervised baselines trained on specific datasets to the pretrained Lag-Llama zero-shot performance on the unseen datasets, and to finetuned Lag-Llama on the respective unseen datasets. In the zero-shot setting, Lag-Llama achieves comparable performance to all baselines, with an average rank of 6.714. On fine-tuning, Lag-Llama achieves state-of-the-art performance in 3 datasets, while performance increases significantly in all other datasets. Most importantly, on fine-tuning, Lag-Llama achieves the best average rank of 2.786, with a significant difference of 2 points over the best supervised model, which suggests that if one had to choose a method to use without prior knowledge of the data, Lag-Llama would be the best option. This clearly establishes Lag-Llama as a strong foundation model that can be used on a wide range of downstream datasets, without prior knowledge of these data distribution — a key property that a foundation model should satisfy.
We now take a deeper dive into Lag-Llama’s performance analysis. Evaluated zero-shot, Lag-Llama achieves strong performance, notably in the platform-delay and weather datasets, where it is especially close to baselines. With fine-tuning, Lag-Llama consistently improves performance compared to inferring zero-shot. In 3 datasets - namely, ETT-M2, weather, and requests — finetuned version of Lag-Llama achieves a significantly lower error than all the baselines, becoming the state-of-the-art. On the exchangerate dataset coming from an entirely new domain, exhibiting a new unseen frequency, Lag-Llama has comparable zero-shot performance, and when finetuned achieves performance similar to the state-of-the-art. This establishes that Lag-Llama performs well across frequencies and domains from which the model may or may not have seen similar data on during pretraining. Lag-Llama achieves a better average rank both in the zero-shot and finetuned setups compared to the Informer, AutoFormer, and ETSFormer models, all of which use complex inductive biases to model time series, compared to Lag-Llama which uses a simple architecture, lags and covariates, along with large-scale pretraining. Our observations suggest that at scale, when used similarly to Lag-Llama, vanilla decoder-only transformers outperform other transformer architectures. We point out that similar results have been shown in the NLP community (Tay et al., 2022) studying the influence of inductive bias at scale, however, we emphasize that we are the first to point out such a result for time series, potentially opening doors to further studies in time series that analyse the influence of inductive bias at scale. Next, compared to the OneFitsAll model (Zhou et al., 2023b) which adapts a pretrained LLM for forecasting, Lag-Llama achieves significantly better performance in all datasets, except for the dataset beijing-pm2.5, where it performs similarly to the baseline, while achieving a much better average rank than this model. These results demonstrate the potential of foundation models trained from scratch on a large and diverse collection of time series datasets when compared to the adaptation of pretrained LLMs, as in the OneFitsAll model (Zhou et al., 2023b). A detailed investigation of the advantages and disadvantages of adapting LLMs versus training time series foundation models from scratch is left as a direction for future work.
We further visualize the forecasts produced by Lag-Llama on the unseen datasets qualitatively in App. §E. Lag-Llama produces forecasts that closely match the ground truth. Further, comparing the forecasts produced by the model in the zero-shot (Fig. 8) and fine-tuned (Fig. 11) settings, one can clearly see that the quality of forecasts increase significantly when the model is fine-tuned.
6.2. Few-Shot Adaptation Performance on Unseen Data
We restrict the data to only the last K% of the history from the training set of the datasets, where we set K to 20, 40, 60, 80 percentages respectively. We train the supervised methods from scratch on the available data, while we fine-tune Lag-Llama. Results are presented in Tab. 2. Across varying levels of history being available for adaptation, Lag-Llama achieves the best average rank across all levels, which establishes Lag-Llama as one with strong adaptation capabilities across all levels of data. As the amount of history available increases, Lag-Llama achieves increasingly better performance across all datasets, and the gap between the rank of Lag-Llama and the baselines widens, as expected. Note, however, that Lag-Llama is most often outperformed by TFT in the exchange-rate dataset, which is from an entirely new domain and has a new unseen frequency. Our observation demonstrates that, in cases where the data is most dissimilar, as compared to the pretraining corpus, Lag-Llama requires increasing amounts of history to train on, and, when given enough history to adapt, performs comparable to state-of-the-art (as discussed in subsection 6.1).
Overall, our empirical results demonstrate that Lag-Llama has strong few-shot adaptation capabilities, and that, based on the characteristics of the downstream dataset, Lag-Llama can adapt and generalize with the appropriate amount of data.
7. Analysis
7.1. Data Diversity
Although loss has been found to scale with pre-training dataset size (Kaplan et al., 2020), it remains unclear what other properties of pre-training datasets lead to desirable model behaviour, despite some initial research in this direction (Chan et al., 2022). Notably, diversity in the pretraining data has contributed to improved zero-shot performance and few-shot adaptation (Brown et al., 2020b), notwithstanding the absence of an adequate definition.
To quantify the diversity of the pretraining corpus, we analyze the properties of its datasets through 22 Canonical time series Characteristics (“catch22 features”), a set of quickly computable time series features selected for their classification ability (Lubba et al., 2019) from the features of the Highly Comparable Time Series Analysis (hctsa) library (Fulcher et al., 2013). To assess diversity across datasets, we apply PCA to the features averaged per-dataset and plot the top 2 components . We find that having multiple datasets within domains and across domains increases the diversity of AC22 features in the top 2-component space (see Figure 12 in Appendix).
7.2. Scaling Analysis
Dataset size has been shown empirically to improve performance (Kaplan et al., 2020). Constructing neural scaling laws (Kaplan et al., 2020; Caballero et al., 2023) can help understand how the performance of the model scales with respect to different parameters such as the amount of pretraining data, number of parameters in the model etc. Towards understanding these quantities for models such as Lag-Llama, we fit neural scaling laws (Caballero et al., 2023) to our model’s validation loss and present in App. §F.1 the obtained scaling laws that describe the performance of our model with respect the amount of pretraining data.
8. Discussion
We present Lag-Llama, a foundation model for univariate probabilistic time series forecasting based on a simple decoder-only transformer architecture. We show that Lag-Llama, when pretrained from scratch on a large corpus of datasets, has strong zero-shot generalization performance on unseen datasets, and performs comparably to dataset-specific models. Lag-Llama also demonstrates state-of-the-art performance across diverse datasets from different domains after finetuning, and emerges as the best general-purpose model without any knowledge of downstream datasets. Lag-Llama also demonstrates a strong few-shot adaptation performance across varying amounts of data history being available. Finally, we investigate the diversity of the pretraining corpus used to train Lag-Llama.
Our work opens up several potential directions for future work. For now, collecting and collating a large scale time series corpus of open dataset would be of high value, since the largest time series dataset repositories (Godahewa et al., 2021) are themselves too small. Further, scaling up the models further beyond the model sizes explored in this work using different training strategies constitutes an essential next step towards building even more powerful time series foundation models. Finally, expanding our work from univariate towards multivariate approaches by capturing complex multivariate dynamics of real-world datasets also constitutes an important direction for future work.
'*Paper Writing 1 > Related_Work' 카테고리의 다른 글