-
[MOIRAI] Unified Training of Universal Time Series Forecasting TransformersPaper Writing 1/Related_Work 2024. 10. 17. 15:42
https://arxiv.org/pdf/2402.02592
https://github.com/SalesforceAIResearch/uni2ts
(Feb 2024)
Abstract
Deep learning for time series forecasting has traditionally operated within a one-model-per-dataset framework, limiting its potential to leverage the game-changing impact of large pre-trained models. The concept of universal forecasting, emerging from pre-training on a vast collection of time series datasets, envisions a single Large Time Series Model capable of addressing diverse downstream forecasting tasks. However, constructing such a model poses unique challenges specific to time series data: i) cross-frequency learning, ii) accommodating an arbitrary number of variates for multivariate time series, and iii) addressing the varying distributional properties inherent in large-scale data. To address these challenges, we present novel enhancements to the conventional time series Transformer architecture, resulting in our proposed Masked EncOder-based UnIveRsAl TIme Series Forecasting Transformer (MOIRAI). Trained on our newly introduced Large-scale Open Time Series Archive (LOTSA) featuring over 27B observations across nine domains, MOIRAI achieves competitive or superior performance as a zero-shot forecaster when compared to full-shot models. Code, data, and model weights can be found at https://github. com/SalesforceAIResearch/uni2ts.
1. Introduction
In the era of foundation models (FMs) (Bommasani et al., 2021), the landscape of deep learning for time series forecasting is experiencing a revolution. In contrast to FMs capable of tackling a multitude of downstream tasks, the current deep forecasting paradigm, involving training a model on a single dataset with a fixed context and prediction length, appears increasingly antiquated, lacking the capacity to generalize or adapt to diverse scenarios or datasets. Given the unreasonable effectiveness of large pre-trained models in improving performance and data efficiency via transfer learning in modalities like vision and language (Dosovitskiy et al., 2020; Brown et al., 2020), we are starting to see a push to transition away from the existing paradigm, towards a universal forecasting paradigm (see Figure 1), where a single large pre-trained model is able to handle any time series forecasting problem. However, the road to building a universal time series forecasting model is mired with challenges.
Unlike the modalities of vision and language which have the unified formats of images and text respectively, time series data is highly heterogeneous. Firstly, the frequency (e.g. minutely, hourly, daily sampling rates) of time series plays an important role in determining the patterns present in the time series. Cross-frequency learning has been shown to be a challenging task due to negative interference (Van Ness et al., 2023), with existing work simply avoiding this problem for multi-frequency datasets by learning one model per frequency (Oreshkin et al., 2020). Secondly, time series data are heterogeneous in terms of dimensionality, whereby multivariate time series can have different number of variates. Furthermore, each variate measures a semantically different quantity across datasets. While considering each variate of a multivariate time series independently (Nie et al., 2023; Ekambaram et al., 2023) can sidestep this problem, we expect a universal model to be sufficiently flexible to consider multivariate interactions and take into account exogenous covariates. Thirdly, probabilistic forecasting is a critical feature often required by practitioners, yet, different datasets have differing support and distributional properties – for example, using a symmetric distribution (e.g. Normal, Student-T) as the predictive distribution is not suitable for positive time series – making standard approaches of pre-defining a simple parametric distribution (Salinas et al., 2020) to be insufficiently flexible to capture a wide variety of datasets. Lastly, a large pre-trained model capable of universal forecasting requires a large-scale dataset from diverse domains. Existing time series datasets are insufficiently large to support the training of such models.
Starting from a masked encoder architecture which has been shown to be a strong candidate architecture for scaling up pre-trained time series forecasting models (Woo et al., 2023), we alleviate the above issues by introducing novel modifications which allows the architecture to handle the heterogeneity of arbitrary time series data. Firstly, we propose to learn multiple input and output projection layers to handle the differing patterns from time series of varying frequencies. Using patch-based projections with larger patch sizes for high-frequency data and vice versa, projection layers are specialized to learn the patterns of that frequency. Secondly, we address the problem of varying dimensionality with our proposed Any-variate Attention, which simultaneously considers both time and variate axes as a single sequence, leveraging Rotary Position Embeddings (RoPE) (Su et al., 2024), and learned binary attention biases (Yang et al., 2022b) to encode time and variate axes respectively. Importantly, Any-variate Attention allows the model to take as input arbitrary number of variates. Thirdly, we overcome the issue of requiring flexible predictive distributions with a mixture of parametric distributions. Furthermore, optimizing the negative log-likelihood of a flexible distribution has the added benefit of being competitive with target metric optimization (Awasthi et al., 2022), a powerful feature for pre-training universal forecasters, given that it can be evaluated with any target metric subsequently.
To power the training of our Large Time Series Model (LTM), we introduce the Large-scale Open Time Series Archive (LOTSA), the largest collection of open time series datasets with 27B observations across nine domains. We optimize the negative log-likelihood of the mixture distribution, and randomly sample context and prediction lengths during training, allowing for flexible downstream usage of the pre-trained model. We train our proposed method, Masked EncOder-based UnIveRsAl TIme Series Forecasting Transformer (MOIRAI1 ), in three sizes – MOIRAI_Small, MOIRAI_Base, and MOIRAI_Large, with 14m, 91m, and 311m parameters respectively. We perform experimental evaluations on both in and out-of-distribution settings, and show that MOIRAI consistently achieves competitive or superior performance compared to state-of-the-art full-shot baselines. Our contributions are summarized as follows:
1. We introduce a novel Transformer architecture to support the requirements of universal forecasting. Crucially, the components we propose extend beyond masked encoders and are versatile, applicable to a broad range of Transformer variants. 2. We introduce LOTSA, a new large-scale collection of open time series datasets to empower pre-training of LTMs. LOTSA, the model weights, and our library for unified training of universal time series models, UNI2TS, will be fully open sourced. 3. Trained on LOTSA data, MOIRAI achieves competitive or superior performance as a zero-shot forecaster when compared to full-shot models.


2. Related Work
Pre-training for Zero-shot Forecasting
Table 1 provides a summary of the key differences between recent pre-trained models with zero-shot forecasting capabilities, which is a recently emerging field. TimeGPT-1 (Garza & MergenthalerCanseco, 2023) first presented a closed-source model, offering zero-shot forecasting capabilities as well as supporting fine-tuning through an API, currently only available to their beta users. ForecastPFN (Dooley et al., 2023) proposes to pre-train on synthetic time series, which can be subsequently be leveraged as a zero-shot forecaster, albeit specialized for data or time limited settings. Lag-llama (Rasul et al., 2023) works towards a foundation model for time series forecasting, leveraging the LLaMA (Touvron et al., 2023) architecture design with lagged time series features, and also presents neural scaling laws for time series forecasting. TimesFM (Das et al., 2023b) is a patch-based decoder-only foundation model for time series forecasting, introducing a larger output patch size for faster decoding. They collected a massive amount of data from Google Trends and Wiki pageviews to pre-train their model in combination with opendata. Tiny Time Mixers (TTMs) (Ekambaram et al., 2024) is a concurrent work leveraging lightweight mixer-style architecture. They perform data augmentation by downsampling high-frequency time series, and support multivariate downstream tasks by fine-tuning an exogenous mixer. leverage Large Language Models (LLMs), pre-trained on web-scale text data, have been leveraged for zero-shot forecasting. Specifically, LLMTime (Gruver et al., 2023) treats time series as strings, applying careful pre-processing based on the specific LLMs’ tokenizer, showing that LLMs have the inherent capability to perform zero-shot forecasting.
Pre-train + Fine-tune for Time Series Forecasting
Pre-training with subsequent fine-tuning on downstream forecasting tasks has predated the recent zero-shot forecasting efforts. Denoising autoencoders (Zerveas et al., 2021) and contrastive learning (Yue et al., 2022; Woo et al., 2022) have been shown to be effective pretext tasks for time series forecasting, but have largely been applied to the existing paradigm of pre-training and fine-tuning on the same dataset, without exploring their generalization capabilities. More recently, Dong et al. (2023) explored combining both reconstruction and contrastive based pre-training approaches, and performed initial explorations into cross-dataset transfer. The topic has been well explored, and we refer readers to more comprehensive surveys (Zhang et al., 2023; Ma et al., 2023). “Reprogramming” is a recent direction which involves fine-tuning the model weights of an LLM which has been pre-trained on text data, for downstream tasks for other modalities. Zhou et al. (2023); Jin et al. (2023) introduce modules and fine-tuning methods to adapt LLMs for time series tasks including forecasting. Liu et al. (2024) has explored leveraging pre-trained LLMs on the cross-dataset setting.
3. Method


3.1. Architecture
Illustrated in Figure 2, MOIRAI follows a (non-overlapping) patch-based approach to modeling time series with a masked encoder architecture. One of our proposed modifications to extend the architecture to the any-variate setting is to “flatten” multivariate time series, considering all variates as a single sequence. Patches are subsequently projected into vector representations via a multi patch size input projection layer. The [mask] signifies a learnable embedding which replaces patches falling within the forecast horizon. The output tokens are then decoded via the multi patch size output projection into the parameters of the mixture distribution. While not visualized, (non-learnable) instance normalization (Kim et al., 2022) is applied to inputs/outputs, aligning with the current standard practice for deep forecasting models. The core Transformer module is an encoder-only Transformer architecture, leveraging various improvements as proposed by recent state-of-the-art LLM architectures. We use pre-normalization (Xiong et al., 2020) and replace all LayerNorms with RMSNorm (Zhang & Sennrich, 2019), and also apply query-key normalization (Henry et al., 2020). The non-linearity in FFN layers are replaced with SwiGLU (Shazeer, 2020), adjusting the hidden dimension to have equal number of parameters as the original FFN layer. We omit biases in all layers of the Transformer module.
3.1.1. Multi Patch Size Projection Layers
In the context of universal forecasting, a single model should possess the capability to handle time series spanning a wide range of frequencies. Existing patch-based architectures rely on a single patch size hyperparameter, a legacy feature from the prevailing one-model-per-dataset paradigm. Instead, we aim for a more flexible strategy: opting for a larger patch size to handle high-frequency data, thereby lower the burden of the quadratic computation cost of attention while maintaining a long context length. Simultaneously, we advocate for a smaller patch size for low-frequency data to transfer computation to the Transformer layers, rather than relying solely on simple linear embedding layers. To implement this approach, we propose learning multiple input and output embedding layers, each associated with varying patch sizes. The selection of the appropriate patch size for a given time series frequency relies on pre-defined settings (see Appendix B.1). Note that we only learn one set of projection weights per patch size, which is shared amongst frequencies if there is an overlap based on the settings.

3.1.2. Any-Variate Attention
Universal forecasters must be equipped to handle arbitrary multivariate time series. Existing time series Transformers often rely on an independent variate assumption or are limited to a single dimensionality due to embedding layers mapping R dy → R dh , where R dh is the hidden dimension. We overcome this limitation as shown in Figure 2, by flattening a multivariate time series to consider all variates as a single sequence. This introduces a new requirement of having variate encodings to enable the model to disambiguate between different variates in the sequence. Furthermore, we need to ensure that permutation equivariance w.r.t. variate ordering, and permutation invariance w.r.t. variate indices are respected. Conventional approaches like sinusoidal or learned embeddings do not meet these requirements, and are unable to handle an arbitrary number of variates. To address this, we propose Any-variate Attention, leveraging binary attention biases to encode variate indices.
Dropping layer and attention head indices, and scaling factor for brevity, the attention score between the (i, m)-th query where i represents the time index and m represents the variate index, and the (j, n)-th key, Aij,mn ∈ R, is given by:


3.1.3. Mixture Distribution
To achieve the goal of having a flexible distribution, yet ensuring that operations of sampling and evaluating the loss function remains simple, we propose to use a mixture of parametric distributions. A mixture distribution of c components has p.d.f.:

3.2. Unified Training
3.2.1. LOTSA Data
Existing work has predominantly relied on three primary sources of data – the Monash Time Series Forecasting Archive (Godahewa et al., 2021), datasets provided by the GluonTS library (Alexandrov et al., 2020), and datasets from the popular long sequence forecasting benchmark (Lai et al., 2018; Wu et al., 2021). While Monash and GluonTS comprise of datasets from diverse domains, they are constrained in size, with approximately 1B observations combined. In comparison, LLMs are trained on trillions of tokens. Das et al. (2023b) builds a private dataset mainly based on Google Trends and Wiki pageviews, but lacks diversity in terms of the domains these time series originate from.
The effectiveness of FMs heavily stem from large-scale pretraining data. Given that existing data sources fall short of supporting such a paradigm, attempting to train an LTM on them may result in misleading conclusions. Thus, we tackle this issue head-on by building a large-scale archive of open time series datasets by collating publicly available sources of time series datasets. This effort aims to cover a broad spectrum of domains, consolidating datasets from diverse sources with varying formats. We design a unified storage format using Arrow (Richardson et al., 2023) which is ready for deep learning pipelines. The resulting collection, LOTSA, spans nine domains, with a total of 27, 646, 462, 733 observations, with key statistics in Tables 2 and 3, and in-depth details in Appendix A.
3.2.2. Pre-training
As introduced in Equation (1), our pre-training task is formulated to optimize the mixture distribution log-likelihood. The design of both the data distribution and task distribution are two critical aspects of the pre-training pipeline. This design imparts versatile capabilities to our LTM, enabling it to adapt to a range of downstream tasks. This flexibility stands in contrast to the prevailing deep forecasting paradigm, where models are typically specialized for specific datasets and settings.
Data Distribution

Task Distribution
Different from the existing deep forecasting paradigm, we aim to train a model with forecasting capabilities over varying context and prediction lengths. Rather than defining a fixed context and prediction length, we sample from a task distribution, (t, l, h) ∼ p(T |D) which defines the lookback window and forecasting horizon, given a time series. In practice, rather than sampling t, l, h, given a time series, we crop a uniformly sampled window, whose length is uniformly sampled from a range. This range is defined by a minimum sequence length per variate of 2, and a total maximum sequence length of 512. The window is then split into lookback and horizon segments, where the prediction length is uniformly sampled as a proportion (within the range [0.15, 0.5]) of the window. We further augment training by i) uniformly subsampling multivariate time series in the variate dimension, and ii) constructing multivariate time series from sub-datasets with univariate time series, by randomly concatenating them. The number of variates is sampled from a beta-binomial distribution with parameters n = 128, a = 2, b = 5 which supports a maximum of 128 variates, with mean ≈ 37 for efficiency.
Training
We train MOIRAI in three sizes – small, base, and large, with key parameter details listed in Table 4. The small model is trained for 100, 000 steps, while base and large models are trained for 1, 000, 000 steps with a batch size of 256. For optimization, we use the AdamW optimizer with the following hyperparameters, lr = 1e-3, weight decay = 1e-1, β1 = 0.9, β2 = 0.98. We also apply a learning rate scheduler with linear warmup for the first 10, 000 steps, and cosine annealing thereafter. Models are trained on NVIDIA A100-40G GPUs with TF32 precision. We implement sequence packing (Raffel et al., 2020) to avoid large amounts of padding due to the disparity of sequence lengths in the new setting with varying context, prediction, and variate lengths, thereby increasing the effective batch size.

4. Experiments
4.1. In-distribution Forecasting
We first perform an in-distribution evaluation using the Monash benchmark, which aim to measure generalization capability across diverse domains. Described in Appendix A, LOTSA includes the Monash Time Series Forecasting Archive as a source of data. For a large portion of these datasets, we only include the train set, holding out the test set which we now use for in-distribution evaluation. In this evaluation, we consider a standard setting with a context length of 1000, and a patch size of 32 for all frequencies, except for quarterly data with a patch size of 8. Figure 3 summarizes the results based on the normalized mean absolute error (MAE), in comparison with the baselines presented in the Monash benchmark. It is worth noting that each baseline in the Monash benchmark is typically trained individually per dataset or per time series within a dataset. In contrast, MOIRAI stands out by being a single model evaluated across various datasets. Full results as well as a comparison with LLMTime (Gruver et al., 2023) can be found in Appendix D.1.
We observe that MOIRAI outperforms all baselines from the Monash benchmark regardless of model size, displaying the strong in-distribution and cross-domain capabilities arising from our unified training methodology. We highlight that each instance of MOIRAI is a single model evaluated across datasets, compared to baselines for which one model is trained per dataset. Further analysis on computational costs can be found in Appendix D.4.
4.2. Out-of-distribution / Zero-shot Forecasting
Next, we perform an out-of-distribution evaluation on unseen target datasets. Here, MOIRAI is a zero-shot forecaster compared with state-of-the-art full-shot baselines which have been trained on the individual target datasets. While the ideal scenario would be to include other universal forecasters, this proves to be a challenging task. As a nascent field, most universal forecasters currently do not yet have open weights available for evaluation. Furthermore, the problem of comparing zero-shot methods is exacerbated by not having a standard held-out test split, making it challenging to collate a set of datasets which all the models have not been trained on. Thus, we establish the strong zero-shot capabilities of MOIRAI by displaying competitive or stronger results compared with SOTA full-shot methods – datasets used in the following have not been included in LOTSA.

Probabilistic Forecasting
We evaluate on six datasets across energy, transport, climate, and sales domains, following a rolling evaluation setup with stride equal to prediction length. Prediction lengths and number of rolling evaluations are defined for each dataset based on frequency. We report the Continuous Ranked Probability Score (CRPS) and Mean Scaled Interval Score (MSIS) metrics (definitions in Appendix C), comparing against four full-shot baselines – DeepAR (Salinas et al., 2020), PatchTST (Nie et al., 2023), and TiDE (Das et al., 2023a) with Student’s t-distribution prediction heads, and TFT based on quantile prediction (Lim et al., 2021), all implemented with the GluonTS library (Alexandrov et al., 2020), as well as simple baselines AutoARIMA (Garza et al., 2022) and Seasonal Naive (Hyndman & Athanasopoulos, 2018). For each dataset and baseline, we perform hyperparameter tuning on a validation CRPS, and report results averaged over five training runs with different seeds. For MOIRAI, we perform inference time tuning, selecting context length from {1000, 2000, 3000, 4000, 5000} and patch sizes based on frequency, on the validation CRPS. Full details of the evaluation setting can be found in Appendix C.
Table 5 reports the CRPS and MSIS, with full results including deterministic metrics in Appendix D.2. We observe that MOIRAIBase and MOIRAILarge consistently achieve strong zero-shot performance, obtaining either best or second best results for all datasets except Walmart and Istanbul Traffic. Even for these datasets, performance is still close to the best performance, despite being a single zero-shot model compared to baselines which have been tuned and trained on the train sets.
Long Sequence Forecasting
We evaluate on a subset of the popular long sequence forecasting benchmark (Wu et al., 2021), omitting datasets which have datasets from the same source present in our pre-training data and cannot be considered zero-shot. We report the Mean Squared Error (MSE) and MAE, comparing against six state-of-the-art baselines, iTransformer (Liu et al., 2023b), TimesNet (Wu et al., 2023), PatchTST, Crossformer (Zhang & Yan, 2023), TiDE, DLinear (Zeng et al., 2023), SCINet (Liu et al., 2022), and FEDformer (Zhou et al., 2022b). Point forecasts are obtained from MOIRAI by taking the median from the samples of the predictive distribution. Tuning for MOIRAI was based on the average validation MSE across prediction lengths, further including the options between channel indepedent and channel mixing strategies (Nie et al., 2023) for the low dimension datasets (ETT and Weather).
Table 6 reports the average performance across prediction lengths, with full results in Appendix D.3. We observe that MOIRAI achieves strong results compared to full-shot baselines. While MOIRAIBase consistently achieves strong performance across datasets with either best or second-best performance, the large model is less consistent, with slightly weaker but competitive results. The relationship between performance and model size is tenuous in this setting, however, this does not constitute strong evidence against the potential of scaling, since these results are based on models trained on a fixed dataset size and settings. Rather, this calls for more comprehensive neural scaling laws (Kaplan et al., 2020) for LTMs, to build a stronger understanding of their scaling behavior.
4.3. Ablation Study
Architecture
We perform a series of ablations in Table 7, starting from the default MOIRAISmall. Firstly, we ablate the multi patch size component, removing the constraints by allowing any frequency to have any patch size during training, and also simply fixing the patch size to 32. In both cases, we observe a deterioration in normalized MAE. Removing Any-variate Attention and using additive learned embeddings (randomizing variate index during training to encourage permutation invariance) instead, leads to suboptimal results, showcasing the strength of Any-variate Attention. We see similar deterioration when replacing the mixture distribution with a Student’s t-distribution, and further visualize the necessity of flexible distributions for probabilistic forecasts in Figure 4.

Training Methodology
We study the impact of a large and diverse dataset by training MOIRAISmall only on the GluonTS and Monash datasets, observing that diversity of data is critical for cross-domain training even on in-distribution evaluation. Finally, given the same batch size and training iterations, we show that packed training significantly boosts performance. This is because packing increases the effective batch size and increases the number of observations the model is trained on, given the same amount of compute.
4.4. Further Analysis
Context Length
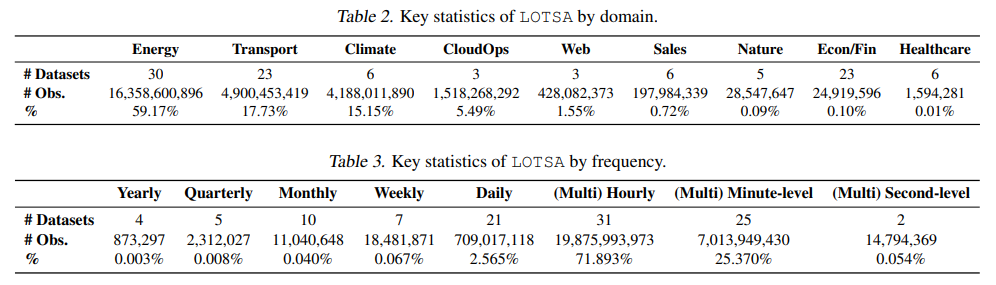
Our pre-training methodology varies context length defined by the task distribution. We verify that MOIRAI has the capability to take as input arbitrary context lengths by visualizing in Figure 5 the relationship between performance and increasing context lengths over three datasets in the zero-shot setting. Zeng et al. (2023); Liu et al. (2023b) previously observed that the desiderata of continuously improving performance with increasing context length is not present in conventional Transformer-based forecasters. Here, we observe that MOIRAI indeed achieves this desired property, in fact, capable of handling thousands of time steps.
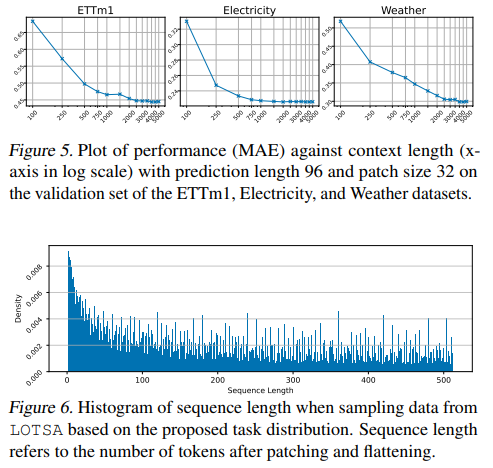
Packing
Packing has long been applied in training LLMs and other Transformer-based models, but not for time series Transformers. While we can get away with inefficiencies when dealing with small-scale data, we start to suffer from longer training times as we scale towards the paradigm of FMs and LTMs. This is further exacerbated by our “flattened” setting which increases the disparity in sequence lengths. As evidenced in Section 4.3, keeping compute (batch size, iterations, etc.) constant, packing improves performance by 16%. To understand why this is the case, we visualize sequence length distribution in Figure 6. With a large portion of the data being shorter than the maximum sequence length, padding represents a whopping 61.08% of input tokens without packed training, and only 0.38% with our packed implementation (calculated over 1000 iterations).
5. Conclusion
In this work, we introduced MOIRAI, a masked encode-rbased universal time series forecasting Transformer which alleviates the issues faced in the universal forecasting paradigm. We also introduce the LOTSA, the largest collection of open-data for pre-training time series forecasting models. MOIRAI is evaluated on the in-distribution and out-of-distribution settings, and is capable of probabilistic and long sequence forecasting. We show that as a zeroshot forecaster, MOIRAI achieves competitive or superior performance compared to full-shot models.
Limitations & Future Work
While MOIRAI achieves phenomenal in and out-of-distribution performance, this is just a first step in the universal forecasting paradigm. Due to resource constraints, little to no hyperparameter tuning was performed – efficient tuning techniques such as µP (Yang et al., 2022a) can be applied. In terms of architecture, our approach to tackling cross-frequency learning with a multi patch size mapping is somewhat heuristic, and future work should design a more flexible and elegant approach. Also, the current architecture has limited support for high-dimensional time series, and efficient methods for extending Transformer input length can alleviate this issue. The masked encoder structure also makes it amenable to exploration of a latent diffusion architecture (Feng et al., 2024). In terms of data, LOTSA can be further enhanced with greater diversity in terms of domain and frequency. Finally, incorporating multi-modality such as tabular or text inputs is an exciting new direction which universal forecasting has unlocked.
A. Large-scale Open Time Series Archive
LOTSA is a collection of time series datasets curated for pre-training of LTMs. In the following, we describe its constituent datasets and their respective sources, listing any pre-processing and data splitting performed. We further details on the key properties of these datasets, providing the domain, frequency, number of time series, number of target variates, number of past covariates (covariates whose values in the forecast horizon are unknown), and total number of observations in the dataset (defined as Summation N i=1 Ti for a dataset with N time series). Of note, if we consider number of observations to include the number of variates, i.e. Summation N i=1 Ti ∗ dyi , LOTSA would have 231,082,956,489 (231B) total observations.
BuildingsBench
BuildingsBench (Emami et al., 2023) (Table 8) provides a collection of datasets for residential and commercial building energy consumption. The BDG-2 datasets, Low Carbon London, SMART, IDEAL, Sceaux, and Borealis are real building energy consumption datasets from various sources. The Electricity dataset (Trindade, 2015) is also included in BuildingsBench but we omit it from LOTSA and use it for out-of-distribution evaluation instead. They further release the Buildings-900K dataset a large-scale dataset of 900K simulated buildings. Emami et al. (2023) introduce a pre-train/test split based on Public Use Microdata Area, but we use include both splits in LOTSA for pre-training. No special pre-processing was applied to these datasets. More information regarding these datasets can be found in Emami et al. (2023).

ClimateLearn
We include the ERA5 and CMIP6 datasets from the ClimateLearn library (Nguyen et al., 2023) (Table 9). The ERA5 and CMIP6 datasets provide time series of various climate related variables such as temperature, and humidity and various pressure levels, based on a grid structure. We use the 2.8125◦ resolution which contains time series in a 64×128 grid.

CloudOps TSF
Woo et al. (2023) introduces three large-scale CloudOps time series datasets (Table 10) measuring various variables such as CPU and memory utilization. We follow their pre-train/test split and only include the pre-train time series in LOTSA, holding out the test set.

GluonTS
The GluonTS library (Alexandrov et al., 2020) provides many datasets popularly used in time series forecasting. We only include the datasets presented in Table 11 as we either hold out the other datasets, or are already included in the Monash repository.

LargeST
LargeST (Liu et al., 2023a) (Table 12) collects the largest dataset from the California Department of Transportation Performance Measurement System (PeMS) (Chen et al., 2001) to date. The PeMS is a popular source of data for many traffic forecasting datasets such as PEMS03, PEMS04, PEMS07, PEMS08, and PEMS Bay, as well as the popular Traffic dataset from (Lai et al., 2018). Since we use such a large amount of dataset from the same source, we can no longer consider forecasting on any of these datasets as an out-of-distribution or zero-shot forecasting task anymore, and thus omit the Traffic dataset of the LSF benchmark from our evaluations.

LibCity
LibCity (Wang et al., 2023a) (Table 13) provides a collection urban spatio-temporal datasets. We drop the spatial aspect of these datsets and consider them as time series data.

Monash
The Monash Time Series Forecasting Repository (Godahewa et al., 2021) (Table 14) is a large collection of diverse time series datasets, the most popular source for building LTMs. We use Monash for in-distribution evaluation, and thus apart from the exceptions listed below, we only include the train region in LOTSA, by holding out the final forecast horizon as the test set. The final forecast horizon is defined for each dataset by (Godahewa et al., 2021). For the following datasets, we include their entirety in LOTSA without a held-out test set for the following reasons:
• London Smart Meters, Wind Farms, Wind Power, Solar Power, Oikolab Weather, Covid Mobility: Originally not included in the Monash benchmark.
• Extended Web Traffic, Kaggle Web Traffic Weekly: We include the extended version of Web Traffic which contains overlap with the original Web Traffic dataset.
• M1 Yearly, M1 Quarterly, M3 Yearly, M3 Quarterly, M4 Yearly, M4 Quarterly, Tourism Yearly: Some time series in these datasets are too short after train/test splits, thus we do not split them (setting a minimum of 16 time steps to achieve at least 2 patches).
We omit Electricity (Trindade, 2015) and Solar (Lai et al., 2018) datasets for out-of-distribution evaluation. Note that the “Weather” from Monash is a different dataset from that used in the out-of-distribution evaluations.

ProEnFo
ProEnFo (Wang et al., 2023b) (Table 15) provides a range of datasets for load forecasting. Unlike BuildingsBench, ProEnFo provides various covariates such as temperature, humidity, and wind speed. We again omit Electricity (Trindade, 2015) which is originally included in ProEnFo for out-of-distribution evaluations.

SubseasonalClimateUSA
The SubseasonalClimateUSA library (Mouatadid et al., 2023) (Table 16) provides climate time series data at a lower granularity (daily) for subseasonal level forecasting. We extract two datasets Subseasonal Precipitation which is the precipitation data from 1948 - 1978, and Subseasonal, which is precipitation and temperature data from 1979 - 2023.

Others
Finally, detailed in Table 17, we further collect datasets from miscellaneous sources not provided by a library or collection. These datasets require more extensive pre-processing since they are not provided by a library, and are raw data instead. We take a standard approach of filtering out time series which are either too short, or have too many missing values. Fo each time series, we consider all variates to be targets, unless otherwise specified by the creators of the dataset (e.g. KDD Cup 2022 is a competition dataset, for which only the “Patv” variate is defined to be the target, with 9 other covariates)

D. Full Experimental Results
D.1. In-distribution Forecasting: Monash Time Series Forecasting Benchmark


We include the full breakdown of results for the Monash benchmark in Table 20, including two versions of LLMTime: GPT3.5 (our reproduction), and LLaMA2 (results from Gruver et al. (2023)). GPT3.5 is our reproduction by running their code5 on the full dataset, using GPT3.5-Turbo-Instruct since text-davinci-003 has been deprecated. LLaMA2 only has results for a subset of datasets in Table 20, thus in Figure 7, we present two aggregated results, one aggregated on the full Table 20, and one on the subset with results available for LLaMA2. As observed, MOIRAI retains the top rankings for with the base and large models in all settings.
D.2. Out-of-distribution forecasting: Probabilistic Forecasting
Table 21 provides the full results of the probabilistic forecasting experiments with additional point forecasting metrics, including the symmetric mean absolute percentage error (sMAPE) (Hyndman, 2014), mean absolute scaled error (MASE) (Hyndman & Koehler, 2006), normalized deviation (ND), and normalized root mean squared error (NRMSE) (Yu et al., 2016).
D.3. Out-of-distribution forecasting: Long Sequence Forecasting
Table 22 provides the full breakdown of results for the long sequence forecasting experiments, listing results for each prediction length.

E. Forecast Visualizations


'Paper Writing 1 > Related_Work' 카테고리의 다른 글