[LLMTime] Large Language Models Are Zero-Shot Time Series Forecasters

https://arxiv.org/pdf/2310.07820

https://github.com/ngruver/llmtime

(Oct 2023)

---

Abstract

By encoding time series as a string of numerical digits, we can frame time series forecasting as next-token prediction in text. Developing this approach, we find that large language models (LLMs) such as GPT-3 and LLaMA-2 can surprisingly zeroshot extrapolate time series at a level comparable to or exceeding the performance of purpose-built time series models trained on the downstream tasks. To facilitate this performance, we propose procedures for effectively tokenizing time series data and converting discrete distributions over tokens into highly flexible densities over continuous values. We argue the success of LLMs for time series stems from their ability to naturally represent multimodal distributions, in conjunction with biases for simplicity, and repetition, which align with the salient features in many time series, such as repeated seasonal trends. We also show how LLMs can naturally handle missing data without imputation through non-numerical text, accommodate textual side information, and answer questions to help explain predictions. While we find that increasing model size generally improves performance on time series, we show GPT-4 can perform worse than GPT-3 because of how it tokenizes numbers, and poor uncertainty calibration, which is likely the result of alignment interventions such as RLHF.

---

1. Introduction

Despite similarities with other sequence modeling problems, such as text, audio, or video, time series has two particularly challenging properties. Unlike video or audio, which typically have consistent input scales and sampling rates, aggregated time series datasets often comprise sequences from radically different sources, sometimes with missing values. Moreover, common applications of time series forecasting, such as weather or financial data, require extrapolating from observations that contain a tiny fraction of the possible information, making accurate point predictions nearly impossible and uncertainty estimation especially important. While large-scale pretraining has become a key element of training large neural networks in vision and text, enabling performance to scale directly with data availability, pretraining is not typically used for time series modeling, where there is no consensus unsupervised objective and large, cohesive pretraining datasets are not readily available. Consequently, simple time series methods (e.g. ARIMA [8], and linear models [53]) often outperform deep learning methods on popular benchmarks [25].

 

In this paper, we demonstrate how large language models (LLM) can naturally bridge the gap between the simple biases of traditional methods and the complex representational learning and generative abilities of modern deep learning. In particular, we introduce an exceedingly simple method, LLMTIME, to apply pretrained LLMs for continuous time series prediction problems, illustrated at a high level in Figure 1. At its core, this method represents the time series as a string of numerical digits, and views time series forecasting as next-token prediction in text, unlocking the use of powerful pretrained models and probabilistic capacities, such as likelihood evaluation and sampling. To enable strong performance, we propose techniques to (1) effectively encode time series as a string of numerical digits and (2) adapt the discrete distributions of LLMs to continuous densities capable of modeling sophisticated multimodal distributions. Using these techniques, we find LLMTIME can exceed or match purpose-built time series methods over a range of different problems in a zero-shot fashion, meaning that LLMTIME can be used without any fine-tuning on the downstream data used by other models.

 

The zero-shot nature of LLMTIME carries several natural advantages: (1) it facilitates the straightforward application of LLMs, eliminating the necessity for specialized knowledge of fine-tuning procedures and the substantial computational resources required for these procedures, as well as sidestepping access issues surrounding proprietary source code or APIs for LLM training or fine-tuning; (2) it is naturally suited to scenarios with limited data availability, where there is little information for training or fine-tuning; (3) by leveraging the broad pattern extrapolation capabilities of extensively pre-trained LLMs, it circumvents the extensive time, effort, and domain-specific expertise typically required for crafting dedicated time series models.

 

To understand the origins of LLMTIME’s impressive performance, we investigate how LLMs express preferences for simple or repetitive sequences [20] and show that these biases are in fact compatible with the salient structure of time series, such as seasonality. Aside from these biases, LLMs also can naturally acccommodate missing data, and express multimodal distributions, which is particularly useful for time series. We also show how LLMs enable appealing functionality, such as the ability to provide additional side information through prompting, and query the LLM to explain its predictions.

 

Finally, in addition to broadly compelling forecasting performance, we find performance tends to improve with scale, and the quality of point predictions also improves with the quality of the uncertainty representation. However, we also find GPT-4 has worse uncertainty calibration than GPT-3, likely due to interventions such as reinforcement learning by human feedback (RLHF).

---

2. Background

Language modeling

bit strings and assigns tokens based on the rate of occurrence in the training corpus, optimizing for shorter sequences of tokens on average. Sampling from a language model typically starts with a prompt, u0:k, and proceeds sequentially using pθ (uj | u0:j−1), which is often preprocessed, for example through temperature scaling or nucleus sampling [26].

Large language models

Brown et al. [9]showed that increasing a language model’s parameter count and training data size leads to new capabilities such as zero-shot generalization, in which a model can perform a text-formatted task without training the model parameters on any task-specific data. Large language models, for example GPT-3 [9] or LLaMA-2 [45], accomplish this form of generalization through in-context learning, which identifies patterns in the language model’s prompt and extrapolates them through next-token prediction. Many authors have speculated that in-context learning emerges from a language model’s extensive compression of the input data [20, 43, 15]. Compression favors learning algorithms that operate over the input data with programmatic abstractions, for example, context-free grammars [2] or induction heads [35], which can implement copy-and-paste type operations for generating samples with highly structured syntax. In this work, we show that the zero-shot generalization abilities of LLMs and their preference for compressible patterns extend well beyond language understanding and can be used for time series forecasting.

 

Zero-shot generalization has made LLMs significantly more useful as assistants, leading to the create of methods to align LLMs with human preferences and instructions, for example reinforcement learning from human feedback (RLHF) [39] and instruction tuning [47]. While key to modern LLMs products, alignment methods can also significantly affect the abilities and calibration of the underlying model [37, 10]. Here we show these methods can also affect forecasting ability.

Time series data

Time series data typically takes the exact same form as language modeling data, as a collection of sequences {Ui = (u1, . . . , uj , . . . , uni )}, but in time series uj is numerical. Because language models are built to represent complex probability distributions over sequences, they are theoretically well-suited for time series modeling. In practice, however, language models are held back by the details of tokenizing numbers. BPE compresses numbers based on frequency of occurrence in the training data, so numbers can be broken down into awkward chunks that make learning basic numerical operations challenging. Touvron et al. [44] therefore designed the LLaMA tokenizer to map numbers to individual digits, which can lead to significant improvements in mathematical abilities, with small LLaMA models outperforming GPT-4 [31].

 

The other challenge of applying language models to time series data is proper evaluation. Mean absolute error (MAE) is commonly used but ignores uncertainty in the forecast which is highly limiting for stochastic data [25, 6]. Continuous ranked probability score (CRPS) captures distributional qualities and can compare models that generate samples without likelihoods. For a single prediction, the CRPS score is defined against the estimated cumulative distribution function (CDF), Fˆ as

where Fˆ(z) is the empirical CDF produced by sampling forecasts and I is the indicator function. While CRPS is an improvement over MAE, it also ignores key structures in the data, such as correlations between time steps. Fortunately, language models can assign likelihoods to full sequences of time series data, and we show how a small modification to an LLM’s discrete likelihood can yield a continuous density that is useful for model comparison.

Language models for time series

Several authors have explored using pretrained language model encoders as initializations for time series models. For example, Zhou et al. [57] propose FPT, which finetunes a BERT encoder to perform time series forecasting. Similarly, Zhang et al. [54] introduce Meta-Transformer, a framework for finetuning a language model for non-text modalities, including time series. Fewer papers explore using LLMs as forecasters without finetuning. The only method we are aware of is PromptCast [51], which poses forecasting as question answering with prompting.

Our work

Unlike methods that leverage LLM backbones, our method is entirely zero-shot and does not require finetuning. Unlike PromptCast, we show that LLMs can be used directly as forecasters without any added text or prompt engineering, if we carefully preprocess the numerical values themselves. Our method solely relies on LLM’s abilities to extrapolate patterns in general sequences and nothing particular to English or any other language. Going beyond prior work, we also cultivate the probabilistic nature of large language models and their ability to capture uncertainty over highly stochastic time series.

---

3. LLMTime: Forecasting with Language Models

Forecasting with LLMTIME has relatively few steps. Once the numerical values are processed into strings, making predictions with the language model follows standard sampling procedures. As we show next, however, correct pre-processing is not always intuitive but is extremely important, and incorrect handling can lead to unusable predictions.

Tokenization

Tokenization is particularly important because it directly influences how patterns form within tokenized sequences and the types of operations that language models can learn. Unfortunately, common tokenization methods like BPE tend to break a single number into tokens that don’t align with the digits, which can make arithmetic considerably more difficult [31]. For example, the number 42235630 gets tokenized as [422, 35, 630] by the GPT-3 tokenizer, and changes by even a single digit can result in an entirely different tokenization. By contrast, in many new open-source LLMs (e.g. LLaMA [44]), numbers are tokenized into individual digits by default. To remedy the tokenization of GPT models, we separate the digits with spaces to force a separate tokenization of each digit and use a comma (" ,") to separate each time step in a time series. Because decimal points are redundant given a fixed precision, we drop them in the encoding to save on context length. Thus, with e.g. 2 digits of precision, we pre-process a time series as follows before feeding into the tokenizer:

In Figure 2, we show that the added spaces of this encoding are helpful for GPT models, preventing the model from getting derailed by outputting an unusual token during sampling. For LLaMA models, with their unique tokenization of numbers, added spaces have the opposite effect. Each digit and space is already assigned its own token, and space tokens become nuisance inputs, adding to the sequence length without simplifying the sequence’s structure and potentially making the sequence out-of-distribution to the model.

Rescaling

To avoid wasting tokens when the inputs are very large, we scale values down so that the α-percentile of rescaled time series values is 1. We avoid scaling by the maximum value so that the LLM can see some fraction of examples (1 − α) where the number of digits changes and reproduce this behavior in its outputs to produce larger values than it has seen. We also experiment with an offset β based calculate as a percentile of the input data, and we tune these two parameters on validation log likelihoods (details in Appendix A).

Sampling / Forecasting

To forecast, draw many samples (e.g. 20) from the LLM and use the statistics of the samples at each time step to construct a point estimate (e.g. as the median) or probabilistic forecast (e.g. as quantiles). To control sampling, we use temperature scaling, logit bias, and nucleus sampling (Appendix C).

Continuous likelihoods

Modeling sequences of individual digits has additional benefits beyond good samples. With n digits of precision in base B, each sequence of n digits after the decimal place corresponds to one of B^n possible bins (Figure 3), each with width B^−n. As each distribution p(uj | u0:j−1; θ) is a softmax over possible digits, we can view the distribution over each individual number as a hierarchical softmax [32], with p(u1, ..., un) = p(un|un−1, ..., u0) p(u1|u0) p(u0). Though a language model’s probability distribution is discrete, we can easily adapt it to provide a continuous density by placing a uniform distribution in each bin. Enumerating each of the countably infinite numbers that the model can produce (because the model can output an arbitrary number of digits before the decimal point) with an index k ∈ N each with probability pk, we can write out the distribution as a mixture of disjoint uniform distributions over the bins

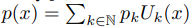
where

Therefore if a given data point lies in bin k, its continuous log likelihood is log p(x) = log pk + n log B. Finally, to obtain the likelihood log p(z) in the original input space, we add a change of variables factor log | dx / dz |, where z → x = s(z) is the rescaling operation in the pre-processing. As a result, the exponentially large number of bins and exponentially small bin widths enabled by our construction make it surprisingly efficient to represent flexible and high-resolution continuous distributions with LLMs, despite using a discrete tokenization of numbers.

Language models as flexible distributions

The fact that LLMs can express flexible distributions over numbers is key for time series data. Uncertainty quantification is essential to forecasting, and typical approaches to representing uncertainty in time series can be limited by misspecification. For example, one common method for creating a probabilistic forecast is to fit a Gaussian or Laplace observation model. When the underlying data distribution is multimodal, both of these models will perform poorly. Methods like Gaussian mixture models (GMMs) solve the issue of multimodality but introduce additional challenges to optimization and model selection. We show that a language model is an underrated solution by training a small autoregressive model on a variety of one-dimensional distributions shown in Figure 3 (right). These distributions come from an exponential random variable, a mixture of a uniform and a student-t distribution, and the heavy-tailed distribution of time series prediction residuals from an ARIMA model on the MonthlyMilk dataset [24]. We evaluate these fits quantitatively by computing Wasserstein distances, and compare to a Laplace observation model, a GMM trained with expectation-maximization, and logistic regression over a flat binning of the data (with a tuned bin size). Each model is trained with only 200 samples from the distribution. The results show that the decimal autoregressive language model (“Decimal AR”) performs extremely well, handling asymmetric, multimodal, and heavy-tailed distributions, which are among the diverse types characteristic of time series data.

---

4. Experiments

We evaluate the zero-shot forecasting ability of LLMs by comparing LLMTIME with GPT-3 and LLaMA-2 70B to many popular time series baselines on a variety of benchmark time series datasets. Not only is LLMTIME able to generate plausible completions of the real and synthetic time series, it achieves higher likelihoods and CRPS values in zero-shot evaluation than the dedicated time series models like ARIMA, TCNs, and N-HiTS. When evaluated on deterministic metrics like MAE, LLMs also perform well, obtain the best or second best MAE values on each benchmark. As we are using LLMs with undisclosed datasets, data leakage is an important concern that we address directly in Appendix B. Beyond strong performance on standard benchmarks, which are the most useful for comparison, we find that LLMTIME also performs well on datasets that could not have been present in the base model’s training data. The full set of hyperparameters used for LLMTIME and the baseline methods are detailed in Appendix C.1. For some of the longer time series, not all of the history can be fit into the context window, and hence hyperparameters implicitly capture the trade-off between higher precision and capturing a larger temporal history.

Datasets

We use three benchmark datasets that are common within deep learning research and many baseline methods that accompany the benchmark datasets.

 

• Darts [24]: A collection of 8 real univariate time series datasets. For Darts, we use several methods that are implemented directly in the package, including neural network models (TCN [29], N-BEATS [38], N-HiTS [11]) and simple moving average models (ARIMA [8]). Darts enables learning observation models with tractable likelihoods and is therefore especially useful for benchmarking the probabilistic predictions of LLMTIME. We also include Spectral Mixture Gaussian Process (SM-GP) [49], a Bayesian nonparametric method (details in Appendix C.1).

 

• Monash [19]: The Monash forecasting archive contains 30 publicly available datasets along with baseline numbers for 12 forecasting models, including simple exponential smooth (e.g. ETS [27]), gradient boosting (e.g. CatBoost [40]) and deep learning models (e.g. DeepAR [41], WaveNet [36]). The Monash archive comprises over 400,000 individual time series, making it infeasible to use in its entirety with the largest available LLMs. To reduce the computational burden, we evaluate GPT-3’s zero-shot performance on 19 datasets described in Appendix C.2.

 

• Informer [55]: We evaluated on multivariate datasets widely used for benchmarking efficient transformer models [16, 55]. In order to predict multivariate data with LLMTIME, we forecast each covariate independently. We baseline against numbers obtained by running public implementations from the Autoformer [50] and FEDFormer [56] codebases (Appendix C.3).

Deterministic results

To compute MAE values for LLMTIME we use the pointwise median of 20 samples from the base model (GPT-2 or LLaMA-2 70B). Figure 4 shows that deterministic predictions from LLMTIME are ranked best or second best on all the considered benchmarks while having no trainable parameters. We provide visualizations of the forecasts in Appendix C.5/C.7/C.8.

Probabilistic results

In Figure 5, we show several probabilistic evaluations on the Darts datasets, including aggregated NLL and CRPS numbers, as well as analysis of how each model reacts to decreasing the input data size. Evaluated on log likelihood and CRPS, LLMTIME considerably outperforms the baselines in aggregate and on almost every individual dataset (results per dataset included in Appendix C.5). Given the analysis of language model-derived densities in Section 3, it is unsurprising that language models excel in probabilistic evaluations, outperforming the baselines even more dramatically. In Figure 5 (left) we show two informative examples that capture the performance of LLMTIME. When extrapolating the AirPassengers dataset, LLMTIME successfully identifies and continues trend and period components, with uncertainty that grows as predictions get further from the input data. On GasRateCO2, LLMTIME replicates local structure when there is relatively little global structure. In Figure 5 (right) we show that LLMTIME not only performs better than baselines with access to the full training data but also when restricted to small fractions of the training data. As time series is frequently characterized by relative data scarcity and challenges in transfer learning, the data efficiency of LLMs is especially attractive.

Comparison with PromptCast

Though included in the results described above, we want to explicitly highlight that LLMTIME significantly outperforms PromptCast [51] when applied to both GPT-3 and LLaMA-2 70B, according to CRPS and MAE aggregated over the Darts datasets. This performance gap highlights important differences between the two approaches. Unlike our method, PromptCast formulates forecasting as a conventional question-answering task in NLP by prompting pre-trained language models with an explicit question about future values in a time series. For example, PromptCast feeds in the prompt “The values in the WoolyDataset for the past 95 time steps are 6172, 6709, 6633, . . . , 6077. What will the values for the next 5 time steps be? The values for the next 5 time steps will be", to extract predictions from an LLM. PromptCast also does not apply our tokenization and data rescaling strategy (Section 3), which we show is crucial for good performance.

---

5. Origins of Zero-Shot Performance

To understand why LLMs can extrapolate time series in a zero-shot manner, let’s take a step back and consider simple numerical sequences, for example [1, 4, 9, 16, . . . ] or [0, 0, 1, 0, 1, 2, 0, 1, 2, 3, . . . ]. For any input sequence, there are arbitrarily many generation rules that are consistent with the input (e.g. f(x) = x^2 for x ∈ [1, 2, 3, 4, ...]), but some generation rules are overly complex and will generalize poorly. LLMs can forecast effectively because they prefer completions derived from simple rules, adopting a form of Occam’s razor prior [20, 43, 15]. To explicitly demonstrate this phenomenon, we create a synthetic example using the function f(x) = x + cos(x) with additive Gaussian noise. We fit symbolic expressions to the first 70% of timesteps using PySR [14] with symbols ["+", "·", "-", "/", "sin", "cos", "exp","square"] to identify generating rules with known complexity, quantified by the number of symbols in the regressed expression (Appendix D). Figure 6 (left) shows the likelihood that GPT-3 assigns the highest likelihood to symbolic regression generating rules that balance consistency with complexity.

 

In Figure 6 (right) we show how program induction in LLMs leads to good zero-shot prediction for many deterministic patterns common in time series data. Along with samples, we also show likelihoods, comparing against standard time series models, which often struggle to extrapolate these simple patterns because they cannot identify a programmatic generation rule to make predictions unlike those seen in the observed history. While the generic simplicity bias is helpful for identifying and extrapolating patterns in the input, a number of patterns common in time series models also translate directly to known capabilities of language models, for example

 

• Repetition bias and periodicity: LLMs’ bias towards repetitive sequences [26] (often unwanted in NLP) corresponds precisely to the ability to identify and extrapolate periodic structure in the input. 4.2, 8.6, 1.0, 4.2, 8.6 will lead to a 1.0 as a likely next output without any time series or arithmetic knowledge (xt = xt−T ).

 

• Arithmetic and trend components: LLMs’ ability to perform addition and multiplication [52, 31] maps on to extrapolating linear and exponential trends. For example, predicting the next element of 0.2, 1.6, 3., 4.4 the LLM needs only to add 1.4 to the last element (xt+1 = xt + c). Similarly, exponential trends have the generating rule xt+1 = c · xt and sigmoid trends have the generating rule xt+1 = xt + cxt(1 − xt).

 

Combining multiple patterns together presents a more difficult challenge, as it requires both identifying the composite pattern and being able to perform the multiple operations within the same token budget. Supposing that a model can perform copying in a single forward pass and addition in a single forward pass, that does not necessarily mean that it can do both simultaneously. We find that GPT-3 is only sometimes able to perform these compositions, though GPT-4 does so more consistently as shown in Appendix E. It is likely that the limitations on compute and tokens spent may make this composition unnecessarily hard, and that additional recursive structure, for example from a scratchpad [34], Chain of Thought (CoT) prompting [48], or adaptive computation [42, 3], would make this task easier.

---

6. Special Properties of LLMs

So far we’ve shown that LLMs are effective forecasters across a variety of datasets and that their forecasting ability arises from biases created by generative pretraining. LLMTIME offers a mechanism for large-scale pre-training that is uncommon in machine learning for time series. LLMs lessen the amount of time series data that must be aggregated for pretraining, substituting text pretraining in its place, and enable more powerful scaling results. Beyond escaping the limits of task-specific data, text pretraining also has many test-time benefits that stem from the base model’s ability to process and generate natural language. As we show in the following section, LLMs can leverage their abilities in order to seamlessly incorporate missing data or answer questions about time series.

Base models and forecasting performance

Given the rapid growth and improvement in opensource LLMs [44, 45], the relationship between LLMTIME forecasting performance and the performance of the underlying base model is particular important and has broad implications. Steady increases in LLM benchmark performance can directly translate to steady improvements in forecasting ability. In Figure 7 (right), we show a study with OpenAI models (davinci, babbage, curie, ada), variants of LLaMA [44] (7B, 13B, 33B, 65B) and LLaMA-2 [45] models (7B, 13B, 70B) measuring accuracy on the Massive Multitask Language Understanding (MMLU) benchmark and probabilistic forecasting error. As we might hope, when reasoning (MMLU) performance increases forecasts also improve.

Chat models

Though convenient scaling relationships appear to hold for base models, the correlation begins to break down when we consider models that have been post-processed for chatbot applications. GPT-4 [37], for example, demonstrates considerably more intelligence than GPT-3 and LLaMA models in natural language tasks, but effectively applying it to time series is challenging. In Figure 7 (center), we show that GPT-4 has a forecasting error (CRPS) significantly larger than GPT-3’s on the Darts datasets. The performance drop is the result of several small details in GPT-4’s method. Due to the altered tokenization, GPT-4 cannot be easily forced to tokenize individual digits into an unbroken stream of numbers. Due to the restrictions on the API, likelihood evaluations are also not permitted, which is why we present results for only CRPS. While GPT-4 can perform well on the synthetic examples discussed in Section 5 (shown in Appendix E), we find that the GPT-4 calibration is much worse than GPT-3’s on stochastic data, likely as a result of the preprocessing details above and the fact that the model has been treated with RLHF [13] which is known to degrade calibration on question-answering tasks [37]. GPT-4 is not the only example of degraded performance in models designed for chat functionality. We observed the same phenomenon in LLaMA-2 models, which have corresponding chat versions for every model size. Figure 7 (right) shows that chat versions tend to have markedly worse forecasting error than their non-chat counterparts, though still maintain trends in size and reasoning ability.

Missing data

A major advantage of treating forecasting as a text completion task and using LLMs is that we can easily feed in any input that can be encoded as text. Often in time series, the time series will be incomplete and certain observations are missing. Simple imputation methods, such as nearest neighbor, are still core pre-processing steps in common data science workflows [33], and the choice of imputation method is especially relevant to clinical data, which often contains irregularly sampled measurements and where missingness can be meaningful signal in itself [28]. Much like humans reading partial reports, LLMs can handle missing values without imputation by adopting special symbols, for instance,

 

. In Figure 8 we compare likelihoods and CRPS value for forecasts from traditional time series methods and LLaMA-2 70B on data that has been corrupted with missing values and then processed with linear interpolation and the above string formatting. While the likelihoods of traditional methods rapidly deteriorate with corruptions, we find that LLaMA-2 70B is more resilient, and when comparing CRPS values, LLaMA-2 70B is competitive with methods that use interpolation.

Connecting time series and textual understanding

Because LLMs are designed for natural language and code, we can augment the numerical time series with useful text. We can do so either by providing textual side information as inputs, or by producing textual outputs from a given time series. An interesting question is whether GPT-4 can explain in text its understanding of a given time series. We probe this quality by providing GPT-4 the code to generate our synthetic time series, provide the values of one these time series, and then ask it to infer which of the functions produced the data in a zero-shot manner. The prediction accuracies are shown in Figure 8, with the three remaining rows all being 0. With CoT [48] prompting the model performs much better than random chance; however, its ability to identify patterns better when directly extrapolating the numerical data, suggesting that its numerical understanding is not fully connected to its textual understanding. In making predictions, the model often explains properties of the time series in order to select the right candidate from the list, and we show several of these sample explanations in Appendix F. We also show how this task is encapsulated in a simple (unprompted) next token prediction problem on cells of a Jupyter notebook, illustrating why we expect such capabilities to emerge with a sufficiently powerful language model.

---

7. Discussion

We have demonstrated that large language models can be used as pretrained time series forecasters by encoding numerical values as text. As with other “foundation” models, pretraining confers useful biases toward generalizable patterns that would otherwise be engineered into the model through architecture design [22], and enables natural scaling of performance with improvements in the base pretrained model. Because LLM forecasters are trained on language, they also confer unconventional capabilities, such as question answering. More broadly, framing time series forecasting as natural language generation can be seen as another step towards unifying more capabilities within a single large and powerful model, in which understanding can be shared between many tasks and modalities. Moreover, zero-shot forecasting can enable broadly compelling performance without requiring significant computational resources, domain expertise, or many downstream training data points.

 

While LLM forecasters benefit from the strengths of pretrained transformers, they also inherit their weaknesses, which can include a limited context window. While many univariate time series problems can fit comfortably within increasingly large context windows, multivariate problems pose a more significant challenge. There have been several recent advances extending LLM context windows to 10-100K tokens [37, 4, 5, 1]. Combining these advances with time series forecasting is a particularly exciting direction for future research. Another potential challenge of using current LLMs architectures could be their weakness in arithmetic and performing recursive and compositional operations, which could be a limitation on particularly challenging time series. On the other hand, many time series do not require precise arithmetic. Understanding the extent to which this is the case, and relaxing this limitation, is also a promising avenue for future research. Separately from any limitation, it would also be promising to investigate effective procedures for fine-tuning LLMs on time series. We hope that bridging LLM research with time series forecasting brings benefits to both communities.

---

Appendix

A. Detailed method and hyperparameters

A.1. Input scaling

For all baseline methods, we use the MinMaxScaler from sklearn. For GPT-3, since it can handle inputs spanning multiple orders of magnitudes by using varying number of digits, we apply an affine transformation to each element xt of a time series (x1, ..., xT ): xt |→ (xt − b)/a, where b = mint xt−β(maxt xt−mint xt), and a is the α-percentile of the shifted series (x1−b, ..., xT −b). We also consider a basic scaler that only applies scaling and not shifting, with a clipped to a maximum of 0.01 when the series only has tiny values. Here α and β are hyperparameters controlling the thresholds at which the number of digits used by the language model changes.

A.2. Validation tuning

We construct a validation time series from the last T observations in the training series, where T is the length of the test series. When the training series is shorter than 2T, we take the last half of the training series as the validation series. The likelihood of generating the validation conditioned on the remaining training series is used to select the hyperparameters. Since LLMTIME is zero-shot, the likelihood is computed without training. For other methods such as ARIMA, the likelihood is computed after training on the remaining training series.

---

B. Addressing Memorization Concerns in GPT-3 Evaluations

Evaluating the performance of black box APIs, like those provided by OpenAI, can be challenging when training data for the underlying models is unknown. In our time series setting, it is natural to wonder if the common benchmark datasets we use are included in the GPT-3 training data. LLMs are known to memorize large amounts of their training data verbatim, including common benchmark text datasets and copyrighted material [7, 12]. Beyond outright memorization, more benign data leakage of closely related data is also possible, leading to overestimation of the generalization performance.

 

Even if our evaluation datasets are present in the GPT-3 training data, it’s unlikely that GPT-3’s good performance is the result of memorization for at least two reasons a priori. First of all, our idiosyncratic formatting is unlikely to be present in the training dataset, even if the numerical values and their order are the same. Second, the time series datasets are unlikely to appear in GPT-3’s training data sufficiently frequently to lead to memorization, as memorization increases in proportion with redundancy [30].

 

To further address the memorization concern, we also perform a direct experiment to show GPT-3 also demonstrates strong performance when evaluated on time series recorded after its training data cutoff date, September 2021. We use the following 3 time series:

 

• Istanbul Traffic (source: https://www.kaggle.com/datasets/leonardo00/istanbul-traffic-index): This dataset provides minute-by-minute Traffic Index data for Istanbul from October 2022 to May 2023. We select the "TI" column and downsample the series to an hourly frequency for the period from May 5th, 2023 to May 18th, 2023, resulting in a total of 267 observations.

 

• TSMC Stock (source: https://www.kaggle.com/datasets/yeemeitsang/tsmc-stock-exchange2022): This dataset contains daily stock market trading data for Taiwan Semiconductor Manufacturing Company Limited for the year 2022. We use the closing price column, which consists of a total of 246 observations.

 

• Turkey Power (source: https://www.kaggle.com/datasets/dharanikra/electrical-power-demandin-turkey): This dataset includes hourly electricity generation and consumption data for Turkey from January 1st, 2020 to December 31st, 2022. We choose the "Total" column and downsample to daily data for the year 2022, resulting in 366 observations.

 

For each time series, we reserve the last 30 observations as test data and perform hyperparameter tuning for each method over the same grid as in Appendix C.1. As displayed in Figure 9, GPT-3 not only predicts plausible continuations of each time series but also competes with or even surpasses the performance of the baseline models in all the tasks, solely based on in-context learning. This result reinforces our belief that GPT-3’s performance is not due to memorization of the test data.

---

C. Benchmarking details and extended results

C.1. Darts datasets

For the Darts datasets, we use the GPyTorch library [17] for Gaussian Process implementation and the Darts libary [24] for ARIMA, TCN, N-BEATS, N-HiTS. We use default values for hyperparameters not described below. The test set is the last 20% of each series.

 

We use several baseline methods implemented directly in Darts [24]:

 

• ARIMA: ARIMA [8], short for AutoRegressive Integrated Moving Average, has been a popular choice for time series forecasting for many decades. ARIMA in Darts wraps code from [18].

 

• TCN: Temporal Convolutional Network (TCN) [29] is residual network with dilated 1D convolutions.

 

• N-BEATS: N-BEATS [38] is a deep learning model tailored for time series forecasting. It employs a deep architecture with backward and forward residual links and stacked fullyconnected layers.

 

• N-HiTS: N-HiTS [11] is a deep learning model that incorporates hierarchical interpolation and multi-rate data sampling techniques in order to create forecasts that emphasize different frequencies and scales of the input signal.

 

We also include Spectral Mixture Gaussian Process (SM-GP) [49] as a Bayesian nonparametric approach to time series modeling.

 

We include the exact hyperparameters for each method below:

 

GPT-3 We perform a grid search over α ∈ [0.5, .7, 0.9, 0.99], β ∈ [0, .15, 0.3, .5], precision (number of decimals) ∈ [2, 3], and temperature = 0.7.

 

GPT-4 Since likelihood evaluation is not available for GPT-4, we fix its hyperparameters for all datasets as follows: we use the basic scaler with α = 0.3 and temperature = 1.0 with top p = 0.8. We do not insert spaces between digits for GPT-4 since it uses a different tokenizer than GPT-3 for which this strategy is not effective.

 

LLaMA For models LLaMA-1 (7B/13B/30B/70B) and LLaMA-2 (7B/7B-chat/13B/13B-chat), we perform a grid search over temperature ∈ [0.2, 0.4, 0.6, 0.8] and use α = 0.99, β = 0.3, precision = 3, nucleus = 0.9. For LLaMA-2 70B and LLaMA-2 70B-chat we use temperature = 1.0, α = 0.99, β = 0.3, precision = 3, nucleus = 0.9.

 

Spectral Mixture Gaussian Process (SM-GP) We use a GP with a kernel formed by the sum of a spectral mixture kernel with 12 mixture components and a RBF kernel. We tune the learning rate from [5e-3, 1e-2, 5e-2, 1e-1].

 

ARIMA We perform a grid search over p ∈ [12, 20, 30], d ∈ [1, 2], and q ∈ [0, 1, 2].

 

TCN We perform a grid search over input_chunk_length ∈ [10, 100, 400], output_chunck_length ∈ [1, 10], kernel_size ∈ [3, 5], num_filters ∈ [1, 3], and likelihood ∈ [Laplace, Gaussian].

 

N-BEATS We perform a grid search over input_chunk_length ∈ [10, 100, 400], output_chunk_length ∈ [1, 10], layer_widths ∈ [64, 16], num_layers ∈ [1, 2], and likelihood ∈ [Laplace, Gaussian].

 

N-HiTS We perform a grid search over input_chunk_length ∈ [10, 100, 400], output_chunck_length ∈ [1, 10], layer_widths ∈ [64, 16], num_layers ∈ [1, 2], and likelihood ∈ [Laplace, Gaussian].

---

C.2. Monash datasets

We evaluate on 19 datasets in Monash that satisfy two criteria:

 

1. The total number of individual series cannot be prohibitively large, so that the experiments can be run in time without access to an enormous cluster and without a gratuitous API expenses.

 

2. The length of the forecasting horizon cannot extend to a length that makes it impossible to fit both the forecast and the history into the context window of the language model.

 

When we applied these criteria, we obtained the following 19 datasets were selected: covid deaths, solar weekly, tourism monthly, australian electricity demand, pedestrian counts, traffic hourly, hospital, fred md, tourism yearly, tourism quarterly, us births, nn5 weekly, nn5 daily, traffic weekly, saugeenday, cif 2016, bitcoin, sunspot.

 

To aggregate across datasets, we normalized the mean absolute error by the MAE achieved by simply predicting the last observed value before the test series (a naive baseline). This normalization places high weight on datasets for which methods perform significantly better or worse than the naive predictor.

 

Several of the baseline methods in the archive are shared with Darts, and all descriptions and code can be found in [19]. A few notable addition include

 

• CatBoost: CatBoost [40] is gradient-boosting framework for continuous or categorical data.

 

• FFNN: A feed-forward neural network with a fixed window of input and output, inspired by Goodfellow et al. [21].

 

• PR: A linear pooled regression (PR) model proposed by Trapero et al. [46].

 

We include visualizations of GPT-3’s prediction on these datasets in Appendix C.7.

 

GPT-3 hyperparameters We use the following hyperparameters for GPT-3: α = 0.9, β = 0,temperature = 0.7. To avoid exceeding the context window, we truncate the history to at most 500 most recent observations. For the baselines, we report their performance as presented in [19]. The normalized MAE values shown in Figure 4 (center) are obtained by normalizing by the lowest baseline MAE on each dataset before aggregating.

 

LLaMA-2 70B hyperparameters We use the following hyperparameters for LLaMA-2 70B: α = 0.99, β = 0.3,temperature = 1.0, nucleus = 0.9. To avoid exceeding the context window, we truncate the history to fit in the LLaMA-2 context window (4096 tokens).

---

C.3. Informer datasets

There are 6 datasets used by Zhou et al. [55] that have become standard benchmarks for evaluating efficient transformers. We evaluate on the 5 datasets that are typically used with a prediction horizon of 96 or 192: “ETTm2”, “exchange_rate”, “electricity”, “traffic”, and “weather”. The results provided in the main text are for a prediction horizon of 96, and we include results for prediction horizon 192 in Appendix C.6. To make evaluation tractable with LLMTIME, we use a smaller evaluation set for each dataset, taking the last 96 or 192 timesteps of each series within each dataset as the test set. As there are many individual series in each multivariate dataset, the number of individual timesteps in the test sets is still substantial. To forecast multivariate series with LLMTIME we simply forecast over each series independently, combine the results, and evaluate as in prior work. Our efficient transformer baselines include

 

• Informer: Informer [55] is an efficient transformer model with sparse attention designed for long sequences.

 

• Reformer: Reformer [55] uses a locality-sensitive hashing mechanism to improve the memory use of attention.

 

• Autoformer: Autoformer [50] is a model design for long time series that replaces standard attention with a mechanism in Fourier space.

 

• FEDformer: Like Autoformer, FEDformer [56] uses frequency-based decompositions to construct an efficient alternative to attention.

 

LLaMA-2 70B hyperparameters We use LLaMA-2 70B with α = 0.99, β = 0.3,temperature = 1.0, nucleus = 0.9, precision = 3. The series in the Informer datasets are very long and we put as much as possible in the LLaMA-2 context window (4096).

---

C.4. Synthetic datasets

For the baselines, we use the same hyperparameter grid in Section C.1. For GPT-3, we didn’t find it useful to perform validation tuning. We use the basic scaler with α = 0.1 and temperature = 0.7.

---

C.5. Darts full probabilistic results

In Figure 10 we show the predicted NLLs and forecasts from LLMTIME using GPT-3 and LLaMA2 70B as base models. LLMTIME typically obtains much better likelihoods than baselines and successfully identifies trend and seasonal components in the time series. We attribute this strong performance in part to the fact that the time series are relatively short. With the tokenization of the input, only about 300 of the observations can fit into the context window, and among the datasets only Sunspots and HeartRate exceed this amount (with 705 and 900 observations respectively).

---

C.6. Informer datasets with extended horizon

Figure 11 shows MAE results per dataset and in aggregate for the Informer datasets we used in the paper. Extending the results in the main text, we also include MAE numbers for a prediction horizon of 192. We observed a similar trend overall, though the relative performance of LLMTIME is slightly diminished, largely due to the “electricity” and “traffic” datasets.

---

C.7. Monash dataset visualizations

Figure 12 shows visualizations of the LLMTIME’s median predictions (GPT-3 base model) on a subset of the Monash datasets.

---

C.8. Informer dataset visualizations

Figure 13 shows visualizations of the LLMTIME’s median predictions (LLaMA-2 70B base model) on the Informer datasets, for a subset of the each set of multivariate series.

---

D. Simplicity bias experiments

We generate data from the function f(x) = cos(x) + x and add Gaussian noise with zero mean and variance 0.05. We fit symbolic expressions to the first 140 timesteps using PySR [14] with symbols ["+", "·", "-", "/", "sin", "cos", "exp","square"] and maxsize = 70, maxdepth = 10, population_size = 50, loss = abs(prediction − target), model_selection = accuracy and niterations = 100. The solutions are saved and ranked by complexity, which is simply the number of terms in the symbolic regression function. The five solutions shown in Figure 6 are

To obtain likelihoods we run GPT-3 (‘text-davinci-003’) with alpha = 0.99, beta = 0.3, basic = True, precision = 1,signed = True.

---

D.1. Full synthetic predictions

Figure 14 shows likelihoods and forecasts from LLMTIME with GPT-3 on the full set of synthetic datasets. We see that some compositional tasks like Linear + Cosine are challenging, while others (Linear * Sine or X * Sine) are well within the abilities of the model. As shown above, GPT-3 demonstrates good understanding of Linear + Cosine through its likelihoods, but has more trouble in sampling. This discrepancy could be the result of good solutions being high likelihood while not being typical.

---

E. GPT-4

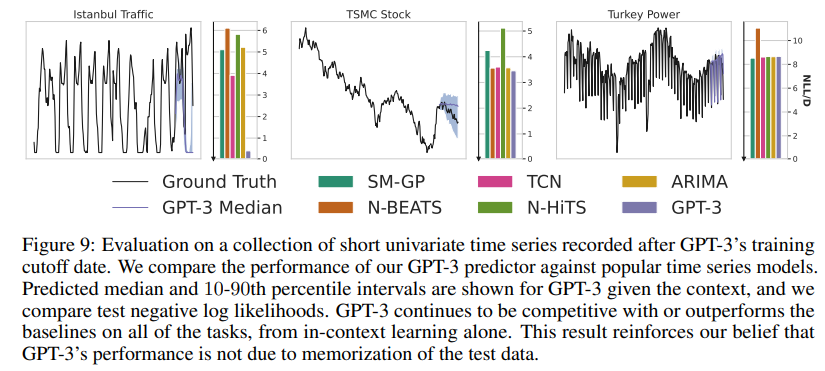
We investigated using GPT-4 for time series prediction. Due to the limitations of the tokenizer, we used the naive tokenization strategy of feeding in the numbers without additional spaces. In addition, due to the enforced separation between system and user in the interface (through additional tokens we cannot modify), inputting the time series input alone leads GPT-4 to talk about the time series or provide analysis, rather than simply continuing the stream of numbers. In order to coax GPT-4 to produce numerical predictions which can be decoded, we added the additional commands System: "You are a helpful assistant that performs time series predictions. The user will provide a sequence and you will predict the remaining sequence. The sequence is represented by decimal strings separated by commas." User: "Please continue the following sequence without producing any additional text. Do not say anything like ’the next terms in the sequence are’, just return the numbers. Sequence:". We found that doing so was sufficient to be able to consistently decode the output numerically for GPT-4, but not for GPT-3.5-turbo.

 

We show predictions on the synthetic benchmarks (from Figure 6) in Figure 15. As one can observe, GPT-4 is considerably better performing on these synthetic benchmarks, although numerical decoding of the model sometimes fails before the full output. With non-deterministic time series problems such as with the DARTS datasets, the predictions are slightly worse than GPT-3, but the uncertainties are much less well calibrated as shown in Figure 16.

---

F. Multimodal Text Understanding of Time Series

We evaluate the ability of the language model to reason about the input time series through text in a zero-shot fashion. To test this, we devise a simple experiment where we generate a synthetic time series from one of several candidate functions. We provide the generation code and the numerical values to GPT-4 (Listing 1), but because of the randomness, GPT-4 must infer which of the functions generated the values. We note that as this code could easily be found within a Jupyter notebook on the internet without intentionally being designed as an experiment for LLMs, we should expect that this textual time series identification task will fall within the data distribution, and in principle should be solved given sufficient capabilities of the language model.

 

To make the problem slightly easier, we add an additional guiding prompt before and after the text in Listing 1. We prepend

 

“The following is code that was run to generate a synthetic time series. From the input and output you will be asked to identify which of the time series was picked to generate the data.”

 

to the code, and after the time series we append either

 

“Which name gave rise to this series? Put your answer in the form ‘Answer: gaussian_wave’ ”

 

or

 

“Carefully analyze the time series. Think step by step, make observations about the time series that you see and then use your observations to identify which of the functions is most likely to have generated it. Reason your way to a solution and at the end give give a name as your answer such as ‘Answer: gaussian_wave’.”

 

for chain-of-thought prompting.

 

The prediction accuracies computed over 20 trials are shown in Figure 8, with x_times_sine, beat, and sinc not shown in the table because GPT-4 predicted these incorrectly 100% of the time. With the CoT prompting, this prediction task elicits some interesting textual analysis of the time series. Several (non cherry-picked) examples are shown below. Notably, this task elicits the model to analyze the time series in text, reasoning about the trend and periodicity. However, the model sometimes makes incorrect deductions about the behavior of the data it has seen, or the expected behavior of the candidate functions.

 

---

References

[1] Joshua Ainslie, Tao Lei, Michiel de Jong, Santiago Ontañón, Siddhartha Brahma, Yury Zemlyanskiy, David Uthus, Mandy Guo, James Lee-Thorp, Yi Tay, et al. Colt5: Faster long-range transformers with conditional computation. arXiv preprint arXiv:2303.09752, 2023.

 

[2] Zeyuan Allen-Zhu and Yuanzhi Li. Physics of language models: Part 1, context-free grammar. arXiv preprint arXiv:2305.13673, 2023.

 

[3] Cem Anil, Ashwini Pokle, Kaiqu Liang, Johannes Treutlein, Yuhuai Wu, Shaojie Bai, J Zico Kolter, and Roger B Grosse. Path independent equilibrium models can better exploit test-time computation. Advances in Neural Information Processing Systems, 35:7796–7809, 2022.

 

[4] Rohan Anil, Andrew M Dai, Orhan Firat, Melvin Johnson, Dmitry Lepikhin, Alexandre Passos, Siamak Shakeri, Emanuel Taropa, Paige Bailey, Zhifeng Chen, et al. Palm 2 technical report. arXiv preprint arXiv:2305.10403, 2023.

 

[5] Anthropic. Introducing 100k context windows. Anthropic blog, 2023. URL https://www. anthropic.com/index/100k-context-windows.

 

[6] Gregory Benton, Nate Gruver, Wesley Maddox, and Andrew Gordon Wilson. Deep probabilistic time series forecasting over long horizons. openreview preprint, 2022. URL https://openreview.net/forum?id=22h1XSEiN0.

 

[7] Stella Biderman, USVSN Sai Prashanth, Lintang Sutawika, Hailey Schoelkopf, Quentin Anthony, Shivanshu Purohit, and Edward Raf. Emergent and predictable memorization in large language models. arXiv preprint arXiv:2304.11158, 2023.

 

[8] George EP Box and Gwilym M Jenkins. Some recent advances in forecasting and control. Journal of the Royal Statistical Society. Series C (Applied Statistics), 17(2):91–109, 1968.

 

[9] Tom Brown, Benjamin Mann, Nick Ryder, Melanie Subbiah, Jared D Kaplan, Prafulla Dhariwal, Arvind Neelakantan, Pranav Shyam, Girish Sastry, Amanda Askell, et al. Language models are few-shot learners. Advances in neural information processing systems, 33:1877–1901, 2020.

 

[10] Sébastien Bubeck, Varun Chandrasekaran, Ronen Eldan, Johannes Gehrke, Eric Horvitz, Ece Kamar, Peter Lee, Yin Tat Lee, Yuanzhi Li, Scott Lundberg, et al. Sparks of artificial general intelligence: Early experiments with gpt-4. arXiv preprint arXiv:2303.12712, 2023.

 

[11] Cristian Challu, Kin G Olivares, Boris N Oreshkin, Federico Garza, Max Mergenthaler, and Artur Dubrawski. N-hits: Neural hierarchical interpolation for time series forecasting. arXiv preprint arXiv:2201.12886, 2022.

 

[12] Kent K Chang, Mackenzie Cramer, Sandeep Soni, and David Bamman. Speak, memory: An archaeology of books known to chatgpt/gpt-4. arXiv preprint arXiv:2305.00118, 2023.

 

[13] Paul F Christiano, Jan Leike, Tom Brown, Miljan Martic, Shane Legg, and Dario Amodei. Deep reinforcement learning from human preferences. Advances in neural information processing systems, 30, 2017.

 

[14] Miles Cranmer. Interpretable machine learning for science with pysr and symbolicregression. jl. arXiv preprint arXiv:2305.01582, 2023.

 

[15] Grégoire Delétang, Anian Ruoss, Paul-Ambroise Duquenne, Elliot Catt, Tim Genewein, Christopher Mattern, Jordi Grau-Moya, Li Kevin Wenliang, Matthew Aitchison, Laurent Orseau, et al. Language modeling is compression. arXiv preprint arXiv:2309.10668, 2023.

 

[16] Dazhao Du, Bing Su, and Zhewei Wei. Preformer: Predictive transformer with multiscale segment-wise correlations for long-term time series forecasting. arXiv preprint arXiv:2202.11356, 2022.

 

[17] Jacob R Gardner, Geoff Pleiss, David Bindel, Kilian Q Weinberger, and Andrew Gordon Wilson. Gpytorch: Blackbox matrix-matrix gaussian process inference with gpu acceleration. In Advances in Neural Information Processing Systems, 2018.

 

[18] Federico Garza, Max Mergenthaler Canseco, Cristian Challú, and Kin G Olivares. Statsforecast: Lightning fast forecasting with statistical and econometric models. PyCon: Salt Lake City, UT, USA, 2022. URL https://github.com/Nixtla/statsforecast.

 

[19] Rakshitha Godahewa, Christoph Bergmeir, Geoffrey I Webb, Rob J Hyndman, and Pablo Montero-Manso. Monash time series forecasting archive. arXiv preprint arXiv:2105.06643, 2021.

 

[20] Micah Goldblum, Marc Finzi, Keefer Rowan, and Andrew Gordon Wilson. The no free lunch theorem, kolmogorov complexity, and the role of inductive biases in machine learning. arXiv preprint arXiv:2304.05366, 2023.

 

[21] Ian Goodfellow, Yoshua Bengio, and Aaron Courville. Deep learning. MIT press, 2016.

 

[22] Nate Gruver, Marc Finzi, Micah Goldblum, and Andrew Gordon Wilson. The lie derivative for measuring learned equivariance. arXiv preprint arXiv:2210.02984, 2022.

 

[23] Dan Hendrycks, Collin Burns, Steven Basart, Andy Zou, Mantas Mazeika, Dawn Song, and Jacob Steinhardt. Measuring massive multitask language understanding. arXiv preprint arXiv:2009.03300, 2020.

 

[24] Julien Herzen, Francesco Lässig, Samuele Giuliano Piazzetta, Thomas Neuer, Léo Tafti, Guillaume Raille, Tomas Van Pottelbergh, Marek Pasieka, Andrzej Skrodzki, Nicolas Huguenin, et al. Darts: User-friendly modern machine learning for time series. The Journal of Machine Learning Research, 23(1):5442–5447, 2022.

 

[25] Hansika Hewamalage, Klaus Ackermann, and Christoph Bergmeir. Forecast evaluation for data scientists: common pitfalls and best practices. Data Mining and Knowledge Discovery, 37(2): 788–832, 2023.

 

[26] Ari Holtzman, Jan Buys, Li Du, Maxwell Forbes, and Yejin Choi. The curious case of neural text degeneration. arXiv preprint arXiv:1904.09751, 2019.

 

[27] Rob J Hyndman, Anne B Koehler, J Keith Ord, and Ralph D Snyder. Forecasting with exponential smoothing: the state space approach. Springer Science & Business Media, 2008.

 

[28] Shruti Kaushik, Abhinav Choudhury, Pankaj Kumar Sheron, Nataraj Dasgupta, Sayee Natarajan, Larry A Pickett, and Varun Dutt. Ai in healthcare: time-series forecasting using statistical, neural, and ensemble architectures. Frontiers in big data, 3:4, 2020.

 

[29] Colin Lea, Rene Vidal, Austin Reiter, and Gregory D Hager. Temporal convolutional networks: A unified approach to action segmentation. In Computer Vision–ECCV 2016 Workshops: Amsterdam, The Netherlands, October 8-10 and 15-16, 2016, Proceedings, Part III 14, pages 47–54. Springer, 2016.

 

[30] Katherine Lee, Daphne Ippolito, Andrew Nystrom, Chiyuan Zhang, Douglas Eck, Chris Callison-Burch, and Nicholas Carlini. Deduplicating training data makes language models better. arXiv preprint arXiv:2107.06499, 2021.

 

[31] Tiedong Liu and Bryan Kian Hsiang Low. Goat: Fine-tuned llama outperforms gpt-4 on arithmetic tasks. arXiv preprint arXiv:2305.14201, 2023.

 

[32] Andriy Mnih and Geoffrey E Hinton. A scalable hierarchical distributed language model. Advances in neural information processing systems, 21, 2008.

 

[33] Steffen Moritz and Thomas Bartz-Beielstein. imputets: time series missing value imputation in r. R J., 9(1):207, 2017.

 

[34] Maxwell Nye, Anders Johan Andreassen, Guy Gur-Ari, Henryk Michalewski, Jacob Austin, David Bieber, David Dohan, Aitor Lewkowycz, Maarten Bosma, David Luan, et al. Show your work: Scratchpads for intermediate computation with language models. arXiv preprint arXiv:2112.00114, 2021.

 

[35] Catherine Olsson, Nelson Elhage, Neel Nanda, Nicholas Joseph, Nova DasSarma, Tom Henighan, Ben Mann, Amanda Askell, Yuntao Bai, Anna Chen, Tom Conerly, Dawn Drain, Deep Ganguli, Zac Hatfield-Dodds, Danny Hernandez, Scott Johnston, Andy Jones, Jackson Kernion, Liane Lovitt, Kamal Ndousse, Dario Amodei, Tom Brown, Jack Clark, Jared Kaplan, Sam McCandlish, and Chris Olah. In-context learning and induction heads. Transformer Circuits Thread, 2022. https://transformer-circuits.pub/2022/in-context-learning-and-inductionheads/index.html.

 

[36] Aaron van den Oord, Sander Dieleman, Heiga Zen, Karen Simonyan, Oriol Vinyals, Alex Graves, Nal Kalchbrenner, Andrew Senior, and Koray Kavukcuoglu. Wavenet: A generative model for raw audio. In 9th ISCA Speech Synthesis Workshop, pages 125–125. ISCA, 2016.

 

[37] OpenAI. Gpt-4 technical report. arXiv, 2023.

 

[38] Boris N Oreshkin, Dmitri Carpov, Nicolas Chapados, and Yoshua Bengio. N-beats: Neural basis expansion analysis for interpretable time series forecasting. Journal of Machine Learning Research, 21(111):1–63, 2020.

 

[39] Long Ouyang, Jeffrey Wu, Xu Jiang, Diogo Almeida, Carroll Wainwright, Pamela Mishkin, Chong Zhang, Sandhini Agarwal, Katarina Slama, Alex Ray, et al. Training language models to follow instructions with human feedback. Advances in Neural Information Processing Systems, 35:27730–27744, 2022.

 

[40] Liudmila Prokhorenkova, Gleb Gusev, Aleksandr Vorobev, Anna Veronika Dorogush, and Andrey Gulin. Catboost: unbiased boosting with categorical features. In Advances in Neural Information Processing Systems, volume 31, pages 6638–6648. NeurIPS, 2018.

 

[41] David Salinas, Valentin Flunkert, Jan Gasthaus, and Tim Januschowski. Deepar: Probabilistic forecasting with autoregressive recurrent networks. International Journal of Forecasting, 36(3): 1181–1191, 2020.

 

[42] Avi Schwarzschild, Eitan Borgnia, Arjun Gupta, Furong Huang, Uzi Vishkin, Micah Goldblum, and Tom Goldstein. Can you learn an algorithm? generalizing from easy to hard problems with recurrent networks. Advances in Neural Information Processing Systems, 34:6695–6706, 2021.

 

[43] Ilya Sutskever. An observation on generalization. Workshop on Large Language Models and Transformers, 2023. URL https://www.youtube.com/watch?v=AKMuA_TVz3A&ab_ channel=SimonsInstitute.

 

[44] Hugo Touvron, Thibaut Lavril, Gautier Izacard, Xavier Martinet, Marie-Anne Lachaux, Timothée Lacroix, Baptiste Rozière, Naman Goyal, Eric Hambro, Faisal Azhar, et al. Llama: Open and efficient foundation language models. arXiv preprint arXiv:2302.13971, 2023.

 

[45] Hugo Touvron, Louis Martin, Kevin R. Stone, Peter Albert, Amjad Almahairi, Yasmine Babaei, Nikolay Bashlykov, Soumya Batra, Prajjwal Bhargava, Shruti Bhosale, Daniel M. Bikel, Lukas Blecher, Cristian Canton Ferrer, Moya Chen, Guillem Cucurull, David Esiobu, Jude Fernandes, Jeremy Fu, Wenyin Fu, Brian Fuller, Cynthia Gao, Vedanuj Goswami, Naman Goyal, Anthony S. Hartshorn, Saghar Hosseini, Rui Hou, Hakan Inan, Marcin Kardas, Viktor Kerkez, Madian Khabsa, Isabel M. Kloumann, A. V. Korenev, Punit Singh Koura, Marie-Anne Lachaux, Thibaut Lavril, Jenya Lee, Diana Liskovich, Yinghai Lu, Yuning Mao, Xavier Martinet, Todor Mihaylov, Pushkar Mishra, Igor Molybog, Yixin Nie, Andrew Poulton, Jeremy Reizenstein, Rashi Rungta, Kalyan Saladi, Alan Schelten, Ruan Silva, Eric Michael Smith, R. Subramanian, Xia Tan, Binh Tang, Ross Taylor, Adina Williams, Jian Xiang Kuan, Puxin Xu, Zhengxu Yan, Iliyan Zarov, Yuchen Zhang, Angela Fan, Melanie Kambadur, Sharan Narang, Aurelien Rodriguez, Robert Stojnic, Sergey Edunov, and Thomas Scialom. Llama 2: Open foundation and fine-tuned chat models. ArXiv, abs/2307.09288, 2023.

 

[46] Juan R Trapero, Nikolaos Kourentzes, and Robert Fildes. On the identification of sales forecasting models in the presence of promotions. Journal of the operational Research Society, 66(2): 299–307, 2015.

 

[47] Jason Wei, Maarten Bosma, Vincent Y Zhao, Kelvin Guu, Adams Wei Yu, Brian Lester, Nan Du, Andrew M Dai, and Quoc V Le. Finetuned language models are zero-shot learners. arXiv preprint arXiv:2109.01652, 2021.

 

[48] Jason Wei, Xuezhi Wang, Dale Schuurmans, Maarten Bosma, Ed Chi, Quoc Le, and Denny Zhou. Chain of thought prompting elicits reasoning in large language models. arXiv preprint arXiv:2201.11903, 2022.

 

[49] Andrew Wilson and Ryan Adams. Gaussian process kernels for pattern discovery and extrapolation. In International conference on machine learning, pages 1067–1075. PMLR, 2013.

 

[50] Haixu Wu, Jiehui Xu, Jianmin Wang, and Mingsheng Long. Autoformer: Decomposition transformers with auto-correlation for long-term series forecasting. Advances in Neural Information Processing Systems, 34, 2021.

 

[51] Hao Xue and Flora D. Salim. Promptcast: A new prompt-based learning paradigm for time series forecasting, 2023.

 

[52] Zheng Yuan, Hongyi Yuan, Chuanqi Tan, Wei Wang, and Songfang Huang. How well do large language models perform in arithmetic tasks? arXiv preprint arXiv:2304.02015, 2023.

 

[53] Ailing Zeng, Muxi Chen, Lei Zhang, and Qiang Xu. Are transformers effective for time series forecasting? arXiv preprint arXiv:2205.13504, 2022.

 

[54] Yiyuan Zhang, Kaixiong Gong, Kaipeng Zhang, Hongsheng Li, Yu Qiao, Wanli Ouyang, and Xiangyu Yue. Meta-transformer: A unified framework for multimodal learning. arXiv preprint arXiv:2307.10802, 2023.

 

[55] Haoyi Zhou, Shanghang Zhang, Jieqi Peng, Shuai Zhang, Jianxin Li, Hui Xiong, and Wancai Zhang. Informer: Beyond efficient transformer for long sequence time-series forecasting. In Proceedings of AAAI, 2021.

 

[56] Tian Zhou, Ziqing Ma, Qingsong Wen, Xue Wang, Liang Sun, and Rong Jin. FEDformer: Frequency enhanced decomposed transformer for long-term series forecasting. In Proc. 39th International Conference on Machine Learning (ICML 2022), 2022.

 

[57] Tian Zhou, Peisong Niu, Xue Wang, Liang Sun, and Rong Jin. One fits all: Power general time series analysis by pretrained lm. arXiv preprint arXiv:2302.11939, 2023.

---