[GPT4TS] One Fits All: Power General Time Series Analysis by Pretrained LM

https://arxiv.org/pdf/2302.11939

(Neurips 2023 Spotlight) (Feb 2023)

---

Abstract

Although we have witnessed great success of pre-trained models in natural language processing (NLP) and computer vision (CV), limited progress has been made for general time series analysis. Unlike NLP and CV where a unified model can be used to perform different tasks, specially designed approach still dominates in each time series analysis task such as classification, anomaly detection, forecasting, and few-shot learning. The main challenge that blocks the development of pre-trained model for time series analysis is the lack of a large amount of data for training. In this work, we address this challenge by leveraging language or CV models, pre-trained from billions of tokens, for time series analysis. Specifically, we refrain from altering the self-attention and feedforward layers of the residual blocks in the pre-trained language or image model. This model, known as the Frozen Pretrained Transformer (FPT), is evaluated through fine-tuning on all major types of tasks involving time series. Our results demonstrate that pre-trained models on natural language or images can lead to a comparable or state-of-the-art performance in all main time series analysis tasks, as illustrated in Figure 1. We also found both theoretically and empirically that the self-attention module behaviors similarly to principle component analysis (PCA), an observation that helps explains how transformer bridges the domain gap and a crucial step towards understanding the universality of a pre-trained transformer. The code is publicly available at https://github.com/DAMO-DI-ML/One_Fits_All.

---

1. Introduction

Time series analysis is a fundamental problem Hyndman & Athanasopoulos (2021) that has played an important role in many real-world applications Wen et al. (2022), such as retail sales forecasting Böse et al. (2017); Courty & Li (1999) , imputation of missing data for economic time series Friedman (1962) anomaly detection for industrial maintenance Gao et al. (2020), and classification of time series from various domain Ismail Fawaz et al. (2019). Numerous statistical and machine learning methods have been developed for time series analysis in the past. Inspired by its great success in natural language processing and computer vision Vaswani et al. (2017); Devlin et al. (2019); Dosovitskiy et al. (2021); Rao et al. (2021), transformer has been introduced to various time series tasks with promising results Wen et al. (2023), especially for time series forecasting Lim et al. (2021); Zhou et al. (2022, 2021); Wu et al. (2021); Nie et al. (2022).

 

We have recently witnessed the rapid development of foundation models in NLP. The key idea is to pre-train a large language model from billions of tokens to facilitate model training for downstream tasks, particularly when we have a few, sometimes even zero, labeled instances. Another advantage of foundation models is that they provide a unified framework for handling diverse tasks, which contrasts conventional wisdom where each task requires a specially designed algorithm. However, so far, little progress has been made to exploit pre-trained or foundation models for time series analysis. One main challenge is the lack of the large amount of data to train a foundation model for time series analysis. The largest data sets for time series analysis is less than 10GB Godahewa et al. (2021), which is much smaller than that for NLP. To address this challenge, we propose to leverage pre-trained language models for general time series analysis. Our approach provides a unified framework for diverse time series tasks, such as classification, anomaly detection, forecasting, and few-shot or zero-shot learning. As shown in Figure 1, using the same backbone, our approach performs either on-par or better than the state-of-the-art methods for all main time series analysis tasks. Besides extensive empirical studies, we also investigate why a transformer model pre-trained from the language domain can be adapted to time series analysis with almost no change. Our analysis indicates that the self-attention modules in the pre-trained transformer acquire the ability to perform certain non-data-dependent operations through training. These operations are closely linked to principal component analysis over the input patterns. We believe it is this generic function performed by the self-attention module that allows trained transformer models to be so-called universal compute engine Lu et al. (2022) or general computation calculator Giannou et al. (2023). We support our claims by conducting an empirical investigation of the resemblance in model behaviors when self-attention is substituted with PCA, and by providing a theoretical analysis of their correlation.

 

Here we summarize our key contributions as follows:

 

1. We propose a unified framework that uses a frozen pre-trained language model to achieve a SOTA or comparable performance in all major types of time series analysis tasks supported by thorough and extensive experiments, including time series classification, short/long-term forecasting, imputation, anomaly detection, few-shot and zero-sample forecasting.

 

2. We found, both theoretically and empirically, that self-attention performs a function similar to PCA, which helps explain the universality of transformer models.

 

3. We demonstrate the universality of our approach by exploring a pre-trained transformer model from another backbond model (BERT) or modality (computer vision) to power the time series forecasting.

 

The remainder of this paper is structured as follows. Section 2 briefly summarizes the related work. Section 3 presents the proposed detailed model structure. In Section 4, we conduct a thorough and extensive evaluation of the performance of cross-modality time series analysis using our proposed method in seven main time series analysis tasks compared to various SOTA baseline models. Section 5 presents various ablation studies, and Section 6 demonstrates the universality of our proposed method using pre-trained models with another structure or pre-trained from another modality. In Section 7, we provide a theoretical explanation of the connection between self-attention and PCA. Finally, in Section 8, we discuss our results and future directions. Due to space limit, more extensive discussion of related work, experimental results, and theoretical analysis are provided in the Appendix.

---

2. Related Work

In this section, we provide short reviews of literature in the areas of time series analysis, in-modality transfer learning, and cross-modality knowledge transfer learning. We postpone the discussion of works for end-to-end time series analysis to Appendix B, due to the limited space.

In-modality Transer Learning through pre-trained models

In recent years, a large number of research works have verified the effectiveness of the pre-trained model from NLP, CV to Vision-and-Language (VL). Latest studies for NLP focus on learning contextual word embeddings for downstream tasks. With the increase of computing power, the very deep transformer models have shown powerful representation ability in various language tasks. Among them, BERT Devlin et al. (2019) uses transformer encoders and employs masked language modeling task that aims to recover the random masked tokens within a text. OpenAI proposed GPT Radford & Narasimhan (2018) that trains transformer decoders on a large language corpus and then fine-tunes on task-specific data. GPT2 Radford et al. (2019) is trained on larger datasets with much more parameters and can be transferred to various downstream tasks. Since transformer models can adapt to various inputs, the idea of pre-training can also be well adapted to visual tasks. DEiT Touvron et al. (2021) proposed a teacher-student strategy for transformers with convolution neural networks (CNNs) as the teacher model and achieves competitive performance. BEiT Bao et al. (2022) converts images as visual tokens and successfully uses the BERT model in CV. However, because of the insufficient training sample, there is little research on pre-trained models on general time series analysis that cover all major tasks like CV or NLP domain.

Cross-modality knowledge transfer

Since transformers can handle different modal tasks through tokenizing the inputs to embeddings, it is also an interesting topic whether the transformers have universal representation ability and can be used for transferring between various domains. The VL pre-trained model VLMo Bao et al. (2021) proposed a stagewise pre-training strategy that utilizes frozen attention blocks pre-trained by image-only data to train the language expert. One of the most related works which transfer knowledge from a pre-trained language model to other domains is Lu et al. (2022), which studies the strong performance of a frozen pre-trained language model (LM) compared to an end-to-end transformer alternative learned from other domains’ data. Another relative work for knowledge transfer to the time series is the Voice2series Yang et al. (2021), which leverages a pre-trained speech processing model for time series classification and achieves superior performance. To the best of our knowledge, no previous research has investigated cross-modality knowledge transfer for the time series forecasting task, let alone general time series analysis.

---

3. Methodology

3.1. Model Structure

 

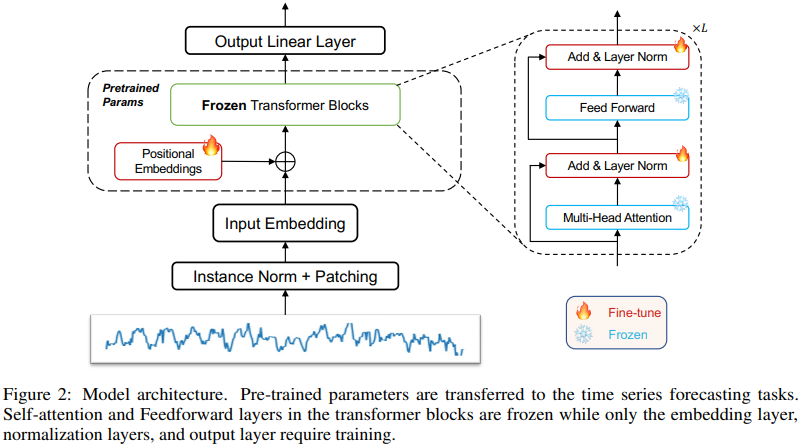
The architecture we employ is depicted in Figure 2. We utilize parameters from NLP pretrained transformer models for time series analysis, with a focus on the GPT2 model Radford et al. (2019). We also experiment with other models, such as BERT Devlin et al. (2019) and BEiT Bao et al. (2022), to further demonstrate that the universal performance of cross-domain knowledge transfer exists in a wide range of pre-trained models.

Frozen Pretrained Block

Our architecture retains the positional embedding layers and self-attention blocks from the pre-trained models. As self-attention layers and FFN (Feedforward Neural Networks) contain the majority of learned knowledge from pre-trained language models, we opt to freeze the self-attention blocks while fine-tuning.

Positional Embeddings and Layer Normalization

To enhance downstream tasks with minimal effort, we fine-tune the positional embeddings and layer normalization layer, which is considered a standard practice Lu et al. (2022); Houlsby et al. (2019). As a result, we retrain these components during fine-tuning.

Input Embedding

Given our goal of applying the NLP pre-trained model to various tasks and a new modality, we must redesign and train the input embedding layer. This layer is responsible for projecting the time-series data to the required dimensions of the specific pre-trained model. To accomplish this, we use linear probing, which also reduces the number of parameters required for training.

Normalization

Data normalization is crucial for pre-trained models across various modalities. In addition to the layer norm utilized in pre-trained LM, we also incorporate a simple data normalization block, reverse instance norm Kim et al. (2022), to further facilitate knowledge transfer. This normalization block simply normalizes the input time series using mean and variance, and then adds them back to the output.

Patching

To extract local semantic information, we utilize patching Nie et al. (2022) by aggregating adjacent time steps to form a single patch-based token. Patching enables a significant increase in the input historical time horizon while maintaining the same token length and reducing information redundancy for transformer models. In our architecture, we apply patching after instance normalization.

---

4. Main Time Series Analysis Tasks

Our proposed method excels in various downstream time series analysis tasks through fine-tuning. To demonstrate the effectiveness of our approach, we conduct extensive experiments on major types of downstream tasks, including time series classification, anomaly detection, imputation, short/long-term forecasting and few-shot/zero-shot forecasting. To ensure a fair comparison, we use GPT2-backbone FPT and adhere to the experimental settings of TimesNet Wu et al. (2023). Due to the space limit, only the summarized results are presented below except zero-shot forecasting. Full experimental results of the other six downstream tasks can be found in Appendix D.3, D.2, D.7, H.6, H.7, H.8, H.9 respectively.

Baselines

We select representative baselines and cite their results from Wu et al. (2023), which includes the most recent and quite extensive empirical studies of time series. The baselines include CNN-based models: TimesNet Wu et al. (2023); MLP-based models: LightTS Zhang et al. (2022) and DLinear Zeng et al. (2023); Transformer-based models: Reformer Kitaev et al. (2020), Informer Zhou et al. (2021), Autoformer Wu et al. (2021), FEDformer Zhou et al. (2022), Nonstationary Transformer Liu et al. (2022), ETSformer Woo et al. (2022), PatchTST Nie et al. (2022). Besides, N-HiTS Challu et al. (2022) and N-BEATS Oreshkin et al. (2019) are used for short-term forecasting. Anomaly Transformer Xu et al. (2021) is used for anomaly detection. XGBoost Chen & Guestrin (2016), Rocket Dempster et al. (2020), LSTNet Lai et al. (2018), LSSL Gu et al. (2021), Pyraformer Liu et al. (2021), TCN Franceschi et al. (2019) and Flowformer Huang et al. (2022) are used for classification.

---

4.1. Main Results

Overall, as shown in Figure 1, GPT2-backbone FPT outperforms other models in most tasks, including long/short-term forecasting, classification, anomaly detection, imputation, and few-shot/zero-short forecasting. This confirms that time series tasks can also take advantage of cross-modality transferred knowledge. In the following, we use GPT2(K) to represent GPT2-backbone with first K Layers.

---

4.2. Imputation

Setups

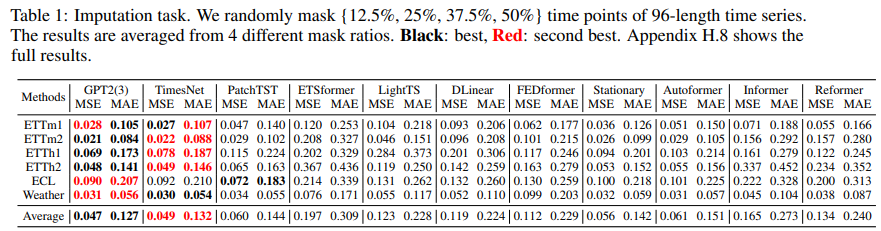
We conduct experiments on six popular real-world datasets, including 4 ETT datasets Zhou et al. (2021) (ETTh1, ETTh2, ETTm1, ETTm2), Electricity and Weather, where the data-missing is common. Following the settings of TimesNet, different random mask ratios ({12.5%, 25%, 37.5%, 50%}) of time points are selected for the evaluation on various proportions of missing data.

Results

The results are shown in Table 1 that GPT2(3) FPT achieves the best performance on most datasets. Particularly, compared to the previous SOTA TimesNet, GPT2(3) FPT yields a relative 11.5% MSE reduction on ETTh1,and a 4.1% MSE reduction on average on six benchmark datasets. It verifies that the proposed method can also effectively mine temporal patterns of incomplete time series.

---

4.3. Time Series Classification

Setups

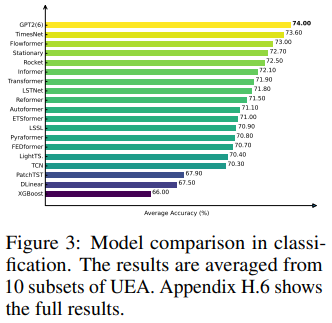
To evaluate the model’s capacity for high-level representation learning, we employ sequence-level classification. Specifically, we follow the same setting as TimesNet: For classification, 10 multivariate UEA classification datasets Bagnall et al. (2018) are selected for evaluation, including gesture, action, audio recognition medical diagnosis and other practical tasks.

Results

As shown in Figure 3, GPT2(6) FPT achieves an average accuracy of 74.00%, surpassing all baselines including TimesNet (73.60%). Specifically, compared to recent published patch-transformer-based models Nie et al. (2022) , GPT2(6) FPT surpasses it by a large margin 9.0% which shows the prior NLP transfer knowledge can indeed help in time series representation.

---

4.4. Time Series Anomaly Detection

Setups

Detecting anomalies in time series is vital in industrial applications, ranging from health monitoring to space & earth exploration. We compare models on five commonly used datasets, including SMD Su et al. (2019), MSL Hundman et al. (2018), SMAP Hundman et al. (2018), SWaT Mathur & Tippenhauer (2016) and PSM Abdulaal et al. (2021). To perform a fair comparison, only the classical reconstruction error is used for all baseline models to the make the setting the same as TimesNet.

Results

Table 2 demonstrates that GPT2(6) FPT also achieves the best performance with the averaged F1-score 86.72%, surpassing previous SOTA method TimesNet by 1.7%. Thus, in addition to its proficiency in representing complete sequences for classification purposes, GPT2(6) FPT is capable of detecting infrequent anomalies within time series.

---

4.5. Long-term Forecasting

Setups

Eight popular real-world benchmark datasets Wu et al. (2023), including Weather, Traffic , Electricity, ILI , and 4 ETT datasets (ETTh1, ETTh2, ETTm1, ETTm2), are used for long-term forecasting evaluation. Additional information regarding the discussion on the input length setting can be found in the appendix H.10.

Results

As shown in Table 3, GPT2(6) FPT achieves comparable performance with PatchTST and outperforms other baselines. Specifically, compared with recent published SOTA method TimesNet, GPT2(6) FPT yields a relative 9.3% average MSE reduction.

---

4.6. Short-term Forecasting

Setups

To fully evaluate different algorithms in forecasting tasks, we also conduct short-term forecasting (with relatively short forecasting horizon) experiments on M4 Makridakis et al. (2018), contains marketing data of various frequencies.

Results

The results in Table 4 show that the performance of GPT2-backbone (6) FPT is superior to advanced Transformer-based and MLP-based models, and comparable to TimesNet and N-BEATS.

---

4.7. Few-shot Forecasting

The large language model (LLM) has demonstrated remarkable performance in both few-shot and zero-shot learning settings Brown et al. (2020); OpenAI (2023). It can be argued that few-shot and zero-shot learning also represent the ultimate tasks for a universal time series forecasting model. To extensively evaluate the representation power of the GPT2(6) for time series analysis, we conduct experiments under few-shot and zero-shot learning settings.

 

Similar to traditional experimental settings, each time series is split into three parts: training data, validation data, and test data. For few-shot learning, only a certain percentage (10%, 5%) timesteps of training data are used.

 

The results of 10% few-shot learning are shown in Table 5. Compared to TimesNet, DLinear, PatchTST and other methods, GPT2(6) FPT achieves the best performance. Traditionally, CNN-based and single MLP-based models are considered more data-efficient for training and suitable for few-shot learning methods. In comparison to convolution-based TimesNet and MLP-based DLinear models, GPT2(6) FPT demonstrates a relative average MSE reduction of 33.3% and 13.5% respectively. We add a comparison with traditional algorithms (ETS, ARIMA, NaiveDrift) in the Appendix D.5 as well, and GTP2(6)FPT also surpass all those traditional methods.

---

4.8. Zero-shot forecasting

This task is used to evaluate the cross datasets adaption ability of our proposed algorithm, i.e. how well a model is able to perform on dataset A (without any training data from A) when it is trained from dataset B.

 

The results are summarized in Table 6. The GPT2(6) FPT model consistently outperforms all recent state-of-the-art transformer and MLP-based time series forecasting methods. Compared to recently published state-of-the-art MLP-based method Dlinear, convolution-based method Timesnet, and transformer-based method Patchtst, GPT2(6)FPT demonstrates a relative average metric reduction of 13.1%,13.6% and 7.3%, respectively. Also, the proposed method is comparable to N-BEATS without any meta-learning design and outperforms N-BEATS in the ELECTR dataset. We attribute this to the knowledge transfer capability from the FPT model.

---

5. Ablations

In this section, we conduct several ablations on model selection and effectiveness of pre-training. The detailed results are shown in Appendix H. We introduce several variants, GPT2(0) FPT, GPT2(6) without freezing and GPT2(6) without pre-training.

Model Selection

We separately analyze the number of GPT2 layers and the fine-tuning parameters selection. The results in Appendix H show that GPT2 with 6-layers is a sound choice compared to full or few layers and partially freezing can avoid catastrophic forgetting, enabling fine-tuning without overfitting.

Effectiveness of Pre-training

The results are shown in Table 7, GPT2(6) FPT outperforms both GPT2(0) FPT and GPT2-random-initialized, suggesting that GPT2 with pre-training parameters can achieve improvement on times series tasks. Besides, GPT2(6) FPT performs better than GPT2- unfrozen, demonstrating that partially freezing also helps. Also, results in Appendix H.2 show that random initialized GPT2(6) with freezing performs poorly and the pre-trained knowledge is instrumental for time series tasks.

---

6. Exploring Transfer Learning from others: The Unexceptional Nature of GPT2-based-FPT

We also present experiments on BERT-backbone FPT Devlin et al. (2019) model and the image-pretrained BEiT-backbone FPT model Bao et al. (2022) to illustrate the generality of pre-trained models for cross-domain knowledge transferring. The results in Table 8 demonstrate that the ability of knowledge transfer is not exclusive to GPT2-based pre-trained language models. Subsequently, our theoretical analysis will shed light on the universality of this phenomenon.

---

7. Training/Inferencing Cost

Analysis of computational cost is helpful for investigating the practicality of the LLM-based model. The results can be found in table 9. Each baseline model comes in two variants, featuring model hidden dimensions of 32 and 768, which align with GPT-2’s specifications. Furthermore, the majority of the baseline models consist of three layers. We assessed the computational cost using a batch from ETTh2 (with a batch size of 128) on a 32G V100 GPU.

 

The results indicate that GPT-2(3) has substantially enhanced time efficiency and reduced parameter quantity compared to baselines with the same model dimension. This was a surprise since we initially anticipated that this large language model might be slower. However, we surmise that the efficient optimization of huggingface’s GPT model implementation primarily accounts for such a significant improvement in time costs. Furthermore, GPT-2(3) and GPT-2(6) demonstrate a mere 6.12% and 4.60% proportion of learnable parameters among the overall parameter size, respectively.

---

8. Towards Understanding the Universality of Transformer: Connecting Self-Attention with PCA

The observation, i.e. we can directly use a trained LM for time series forecasting without having to modify its model, makes us believe that the underlying model is doing something very generic and independent from texts despite it being trained from text data. Our analysis aims to show that part of this generic function can be related to PCA, as minimizing the gradient with respect to the self-attention layer seems to do something similar to PCA. In this section, we take the first step towards revealing the generality of self-attention by connecting the self-attention with principal component analysis (PCA). Moreover, when coming the question of why fine-tuning is restricted to the embedding layer and layer norm, following our hypothesis that the pre-trained LM as a whole performs something generic, partially fine-tuning any of its components may break the generic function and lead to relatively poor performance for time series analysis.

 

For each layer, we calculate and perform statistical analysis of the pairwise token similarity values. Specifically, we denote each output feature map with shape of (b, n, d), where b is the batch size, n is the number of tokens, and d is the dimension of each token feature. We calculate the cosine similarity, and the resulting pairwise similarity matrix of shape (b, n, n). Next we count the number of occurrences of similarity values within each interval as a simple statistical analysis.

 

Our analysis is motivated by the observation that the within-layer token similarity increases with deeper layers in transformer. We report the layer-wise average token cosine similarity on ETTh2 dataset in Figure 4 (a, c), where we mix weights from pre-trained LM with weights randomly sampled from Gaussian distribution. Here we summarize our observations: a) in a randomly initialed GPT2 (6) model, the token similarity is low among all layers (0.1 − 0.2); b) when gradually switched to the pretrained GPT2 model, the token similarity significantly increases in the deep layers and eventually reaches more than 0.9 in the last layer. One potential explanation for the increasing token similarity is that all the token vectors are projected into the low-dimensional top eigenvector space of input patterns. To verify this idea, we further conduct experiments where we replace the self-attention module with PCA and find token similarity patterns remain unchanged according to Figure 4 (b), which further justifies the potential connection between PCA and self-attention.

 

---

9. Conclusions

In this paper, we developed a foundation model for time series analysis, based on pre-trained model from NLP or CV, that can (a) facilitate the model training for downstream tasks, and (b) provide unified framework for diverse time series analysis tasks. Our empirical studies show that the proposed method performs on par or better than the state-of-the-art approaches on almost all time series tasks. We also examine the universality of transformer by connecting self-attention with PCA, an important step towards understanding how generative models work in practice. On the other hand, we do recognize some limitations of our work: the zero-shot performance of our approach is still behind N-beat on several datasets, and our analysis of the generality of transformer is still in the early stage. Moving forward, we plan to improve the performance of our approach by exploiting the parameter efficient fine-tuning approaches which usually introduce additional structures into the pre-trained model for better adaption. To better understand the universality of transformer, we also plan to examine it from the viewpoint of n-gram language model, an approach that is taken by Elhage et al. (2021); Olsson et al. (2022). In Appendix F, we include our initial analysis along this direction.

---