Aligning Language Models with Preferences through f-divergence Minimization

https://arxiv.org/pdf/2302.08215

(Jun 2023 ICML 2023)

 

짜잔~ 종합선물세트 입니다~!

f-divergence로 대동단결.

옛다. 크리스마스 선물 받아랏~!

 

너무 당연한 이야기이지만, 목표를 어떻게 설정하느냐에 따라 인생은 완전히 달라진다.
목적지 변경은 우리를 완전히 다른 방향으로 이끌기도 한다.

objective function (loss function)에 따라서 model의 behavior가 달라지는 건 참 흥미진진하다.

(좀 더 구체적으로는..

- 어떠한 measure로 target distribution을 approximate할 것인가

- metric에 따라 convergence하는 양상은 어떻게 달라지는가)

 

이 논문을 읽는데 왜케 행복하지? ㅜㅜ 

이 논문을 읽기 위해 준비작업을 많이 했어!

그래서 그런가 애착이 가고, 뿌듯하다. 

 

연구가 성숙되어 가는 과정을 쭉 따라온 셈인데, 그 과정이 좋고,

나도 지식이 체계화되고 연구를 어떻게 더 발전시킬 수 있을까 고민할 수 있어서 좋다. 

 

앙 행복하다 ㅠㅠ 배부른 느낌. 

(그렇다고 밥을 안 먹을 껀 아님 ㅎㅎㅎ)

---

Abstract

Aligning language models with preferences can be posed as approximating a target distribution representing some desired behavior. Existing approaches differ both in the functional form of the target distribution and the algorithm used to approximate it. For instance, Reinforcement Learning from Human Feedback (RLHF) corresponds to minimizing a reverse KL from an implicit target distribution arising from a KL penalty in the objective. On the other hand, Generative Distributional Control (GDC) has an explicit target distribution and minimizes a forward KL from it using the Distributional Policy Gradient (DPG) algorithm. In this paper, we propose a new approach, f-DPG, which allows the use of any f-divergence to approximate any target distribution that can be evaluated. f-DPG unifies both frameworks (RLHF, GDC) and the approximation methods (DPG, RL with KL penalties). We show the practical benefits of various choices of divergence objectives and demonstrate that there is no universally optimal objective but that different divergences present different alignment and diversity trade-offs. We show that Jensen-Shannon divergence strikes a good balance between these objectives, and frequently outperforms forward KL divergence by a wide margin, leading to significant improvements over prior work. These distinguishing characteristics between divergences persist as the model size increases, highlighting the importance of selecting appropriate divergence objectives.

---

1. Introduction

Language models (LMs) have recently revolutionized the field of Natural Language Processing thanks to their generative capabilities, which are useful in a vast number of tasks (Brown et al., 2020; Srivastava et al., 2022). However, generated texts can also violate widely-held human preferences, e.g. helpfulness (Askell et al., 2021), nonoffensiveness (Gehman et al., 2020), truthfulness (Lin et al., 2022) or equal treatment (Cao et al., 2022). Aligning LMs with human preferences is the problem of adapting the LM in such a way that generated content is perceived to match the human’s intent (Ouyang et al., 2022) or that it is helpful, honest, and harmless (Askell et al., 2021; Bai et al., 2022b). Fundamentally, an aligned LM can be seen as a desired target distribution that we would like to generate from (Korbak et al., 2022c). Some approaches leave this distribution implicit, to be defined as a side-effect of the proposed intervention. These include prompting with natural language instructions or demonstrations (Askell et al., 2021), using scorers or safety filters while decoding (Roller et al., 2021; Xu et al., 2021), supervised fine-tuning on curated data (Solaiman & Dennison, 2021; Ngo et al., 2021; Welbl et al., 2021; Chung et al., 2022) or selected samples from the model (Zelikman et al., 2022; Scheurer et al., 2022; Dohan et al., 2022), and fine-tuning the language model using reinforcement learning with a learned reward function that approximates human feedback (Reinforcement Learning from Human Feedback or RLHF; Ziegler et al., 2019; Bai et al., 2022a; Ouyang et al., 2022).

 

Instead, Khalifa et al. (2021) propose a framework that they name Generation with Distributional Control (GDC), where they define the target distribution p that represents the aligned LM as an EBM (Energy Based Model), namely an unnormalized version of p that can be evaluated over any input x. They then train the generative model πθ to approximate p via methods such as Distributional Policy Gradients (DPG; Parshakova et al., 2019), which minimize the forward Kullback-Leibler (KL) divergence KL(p||πθ) of p to πθ. The advantage of such an approach is that it decouples the problem of describing the aligned LM from the problem of approximating it. Furthermore, even if RL with KL penalties (Todorov, 2006a; Kappen et al., 2012; Jaques et al., 2017; 2019), the method used to fine-tune a LM in RLHF, is defined only in terms of reward maximization, it has also been shown to be equivalent to minimizing the reverse KL divergence KL(πθ||p) of πθ to a target distribution p that can also be written explicitly in closed-form (Korbak et al., 2022b).

 

The possibility of approximating various distributions according to different divergence measures begs the question: Does the choice of a divergence measure matter? In principle, all divergences lead to the same optimum, namely the target distribution p. However, when we restrict πθ to a certain parametric family that does not include p (i.e., the search space is mis-specified), then the minimum can be found at different points, leading to optimal models with different properties. Moreover, different divergences present different loss landscapes: some might make it easier for stochastic gradient descent to find good minima. Finally, the space of possible divergence measures and forms of target distributions is a vast and largely uncharted terrain. Prior work has largely failed to decouple the form of a target distribution and the algorithm used for approximating it.

 

Here, we introduce f-DPG, a new framework for finetuning an LM to approximate any given target EBM, by exploiting any given divergence in the f-divergences family, which includes not only the forward KL and the reverse KL cited above, but also Total Variation (TV) distance, JensenShannon (JS) divergence, among others. f-DPG generalizes existing approximation techniques both DPG and RL with KL penalties algorithms, thus allowing us to investigate new ways to approximate the target distributions defined by the GDC and RLHF frameworks. In particular, we explore the approximation of various target distributions representing different alignment goals, which include imposing lexical constraints, reducing social bias with respect to gender and religion, enforcing factual consistency in summarization, and enforcing compilability of generated code. We focus our experiments on four instantiations of f-DPG, namely KL-DPG, RKL-DPG, TV-DPG and JS-DPG, whose objective is to minimize the forward KL, reverse KL, TV and JS divergences, respectively, and evaluate each experiment in terms of approximation quality as measured by all of these f-divergences. We show that we can obtain significantly improved results over the original KL-DPG algorithm (Parshakova et al., 2019) by minimizing other f-divergences, even when the approximation quality is evaluated under the lens of the forward KL. Furthermore, we observe that while there is no single best optimization objective for all cases, JS-DPG often strikes a good balance and significantly improves upon prior work (Khalifa et al., 2021; Korbak et al., 2022a), as illustrated in Fig. 1. Lastly, we find that f-DPG with an optimal objective continues to outperform suboptimal objectives as we scale model size from 127M parameters to 1.5B parameters (Sec. 4.5). The smooth and gradual scaling trend observed with increasing model size suggests that our findings will generalize to even larger LMs.

Overall, the contributions of the paper include:

 

1. Introducing f-DPG, a unifying framework for approximating any EBM target distribution by minimizing any f-divergence (Sec. 3.2), and deriving a universal formula for gradient descent with f-divergences (Theorem 1).

 

2. Extending f-DPG to include baselines for variance reduction (Fact 1); and handling conditional target distributions (Fact 2).

 

3. Investigating the performance of f-DPG on a diverse array of thirteen LM alignment tasks, three forms of target distributions, four f-divergence objectives and eight metrics.

---

2. Background

We can organize approaches to LM alignment along two axes: how the target distribution is constructed and how it is approximated. The first problem roughly corresponds to representing human preferences through the specification of a probability distribution and the second to allowing the production of samples from that distribution.

---

2.1. Defining a Target Distribution

The target distribution expresses an ideal notion of an LM, incorporating human preferences, as probabilities p(x) over texts x according to how well they satisfy the preferences. Formally, p(x) is often defined through a non-negative function P(x) (aka an energy-based model or EBM (LeCun et al., 2006)) such that p(x) ∝ P(x). The model P(x) (and p(x) after normalization) can be used to score samples, but not to directly produce them because it lacks an autoregressive form. In the rest of the paper, we will focus on target distributions modeling three types of preferences prominently employed in recent literature about GDC (Khalifa et al., 2021) and RLHF (Ziegler et al., 2019; Stiennon et al., 2020; Ouyang et al., 2022; Menick et al., 2022; Bai et al., 2022a).

Binary preferences

For human preferences naturally expressible as a binary constraint b(x) ∈ {0, 1} (e.g. a sample x must never contain a curse word), Khalifa et al. (2021) proposed the following target distribution:

 

where a is a pretrained LM and b(x) = 0 if x contains a curse and b(x) = 1 otherwise. p_GDC_bin is the distribution enforcing that all samples match the binary constraint, which deviates minimally from a as measured by KL(p_GDC_bin || a).

Scalar preferences

Some human preferences, such as helpfulness, are more naturally expressed as scalar scores. Alignment with respect to these is typically addressed with RLHF (Stiennon et al., 2020; Ziegler et al., 2019; Ouyang et al., 2022), which consists of, first, capturing human preferences as a reward function r(x) (e.g. scores given a reward model trained to predict human preferences) and second, applying RL with KL penalties (Todorov, 2006a; Kappen et al., 2012; Jaques et al., 2017; 2019) to maximize this reward while penalizing departure from a(x):

 

This objective can be equivalently framed as minimizing the reverse KL, KL(πθ||p_RLKL), where the target distribution p_RLKL is defined as:

 

where β is a hyperparameter (Korbak et al., 2022b).

Distributional preferences

Finally, there is a class of distributional preferences (Weidinger et al., 2021) that cannot be expressed as a function of a single sample x but depend on the entire distribution, e.g. a particular gender distribution of persons mentioned in LM samples. Khalifa et al. (2021) model such preferences through distributional constraints using the following exponential family target distribution

 

where ϕi are features defined over texts (e.g. the most frequent gender of people mentioned in x) and λi are coefficients chosen so that the expected values Ex∼p [ϕi(x)] match some desired values µ¯i (e.g., 50% gender balance). The resulting distribution p_GDC-d matches the target feature moments, while deviating minimally from a as measured by KL(p_GDC_dist || a).

---

2.2. Approximating the target distribution

Drawing samples from a target distribution p constitutes the inference problem. There are broadly two approaches to this problem: (i) augmenting decoding from a at inference time to obtain samples from p and (ii) training a new parametric model πθ to approximate p which can then be sampled from directly. The first family of approaches includes guided decoding methods (Dathathri et al., 2020; Qin et al., 2022), Monte Carlo sampling techniques such as rejection sampling to sample from simple distributions like p_GDC_bin (Roller et al., 2021; Ziegler et al., 2022), and Quasi Rejection Sampling (QRS) (Eikema et al., 2022) or MCMC techniques (Miao et al., 2019; Goyal et al., 2022) to sample from more complex distributions, such as p_GDC_dist. In the rest of the paper, we will focus on the second family: methods that train a new model πθ to approximate p by minimizing a divergence measure from p, D(πθ||p). Khalifa et al. (2021) uses Distributional Policy Gradients (DPG; Parshakova et al., 2019) to approximate the target distribution by minimizing KL(p||πθ), or equivalently, CE(p, πθ):

---

3. Formal Aspects

In this section, we describe the f-divergence family, and introduce a generic technique, f-DPG, for minimizing the f-divergence between a target distribution p and a model πθ. We then describe the application of f-DPG to aligning language models with human preferences.

---

3.1. f-divergences

---

하지만 support가 define 되지 않아서 gradient signal을 받지 못한다거나, 혹은 exploding (diverge)해버리는 경우를 excuse했다고 차치하더라도 f-divergence는 여전히 문제를 가지고 있다.

 

* p(x)/q(x)에서 q(x)가 0에 가까워지면 diverge 하게 된다. -> numerically unstable* 그리고 q(x) * f(p(x)/q(x))에서 q(x)가 0에 가까워지면 gradient signal을 받지 못하게 된다. -> ignored (Mode collapse)

 

그리고 Total Variation Distance는 IPM으로도 보아야 하기 때문에 prob distribution 간의 ratio가 아닌 absolute difference를 minimize함으로써 다른 f-divergence와 양상이 달라지는 것에 대하여 생각해보아야 한다.

---

shown that D_f (p1||p2) ≥ 0 for any p1 and p2, with equality if p1 = p2; conversely, if D_f (p1||p2) = 0 and f is strictly convex at 1, then p1 = p2.

 

The f-divergence family includes many important divergence measures, in particular KL divergence KL(p1||p2), reverse KL divergence KL(p2||p1), Jensen-Shannon divergence, and Total Variation distance. We list these fdivergences and their generators in Tab. 1. For more details about notations and properties of f-divergences, see App. A.1 and also Liese & Vajda (2006); Polyanskiy (2019); Sason & Verdu (2016); Sason (2018).

---

3.2. Distributional alignment with f-divergences

Let X be a discrete countable or finite set, in our case a set of texts. Given a target probability distribution p(x) over elements x ∈ X , our goal is to approximate p with a generative model (aka policy) πθ. On the other hand, the generative model πθ is a parametric model, typically an autoregressive neural network, from which we can (i) directly sample and (ii) evaluate probabilities πθ(x).

 

We approach this problem by attempting to minimize the f-divergence of πθ to p: 3

 

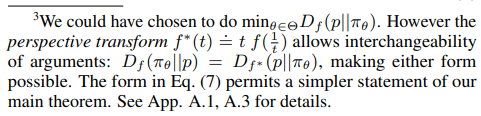
where θ varies inside the parametric family Θ. Note that when the family πθ, θ ∈ Θ is “well-specified”, i.e., when ∃θ0 s.t. p = πθ0 , the true minimum of Eq (7) is 0, attained at θ0, whatever divergence Df is chosen. In contrast, when the family is “mis-specified” i.e. does not include p, the distribution πθ with minimal divergence can be strongly dependent on the chosen divergence Df .

 

Eq. (7) might be solved approximately using stochastic optimization with samples drawn from the distribution p, as the definition of Df (πθ||p) involves taking the expectation with respect to p. However, it is often not possible to sample directly from p, while it is possible to sample from πθ. Our optimization technique is then based on the following core result, which we prove in App. A.3.

 

Theorem 1. Let p and πθ be distributions over a discrete set X such that at least one of the following conditions holds: (i) ∀θ ∈ Θ, Supp(p) ⊂ Supp(πθ), or (ii) Supp(πθ) does not depend on θ. Then:

---

3.3. Adding a baseline

 

Fact 1. Subtracting B from rθ(x) does not introduce bias into f-DPG gradient estimates.

 

Typically, B is chosen to be the average of the rewards, B .= Ex∼πθ [rθ(x)]. In the experiments of Sec. 4, we use the baseline technique where B is an estimate of the average of pseudo-rewards, unless otherwise specified.

---

3.4. Recovering Some Existing Methods

Various existing methods for aligning LM with preferences can be included in the f-DPG framework.

---

3.5. Estimating Z

The target distribution p is often defined as p(x) ∝ P(x), where P(x) is a non-negative function over X . The distribution p can then be computed as p(x) = 1/Z P(x), where

---

3.6. Conditional Target Distributions

For a conditional task such as machine translation, summarization or dialogue, where πθ is defined as a conditional distribution πθ(x|c), we adapt the conditional generalization of DPG introduced in Korbak et al. (2022a). Given a distribution over contexts τ (c) and a map from a context c to a target distribution p_c, we have (see App. E for details):

 

Fact 2. f-DPG is generalized to the conditional case by optimizing the loss

---

4. Experiments

We study four instantiations of f-DPG, namely KL-DPG, RKL-DPG, TV-DPG and JS-DPG, corresponding to minimizing the forward KL, reverse KL, Total Variation, and Jensen-Shannon divergences, respectively. We use an exponential moving average baseline with weight α = 0.99 for all, except for KL-DPG, where we use the analytically computed value of the pseudo-reward expectation, which amounts to 1 (Korbak et al., 2022b). We evaluate them on a diverse array of tasks including imposing sentiment constraints (Sec. 4.1), lexical constraints (Sec. 4.2), debiasing genders’ prevalence and religious groups’ regard (Sec. 4.3), and context-conditioned tasks, such as enforcing factual consistency in summarization (Sec. 4.4) or compilability of generated code (see App. E.1). Unless specified otherwise, we use a pretrained GPT-2 “small” (Radford et al., 2019) with 117M parameters for the initial model. Yet, we demonstrate in Sec. 4.5 that the observations continue to hold for models of larger size. Implementation details and hyper-parameters are available in App. C. 

Metrics

We report the following key metrics. We add task-specific metrics if needed.

 

1. Df (πθ||p), the f-divergence between p and πθ, with four different f’s corresponding to forward KL, KL(p||πθ); reverse KL, KL(πθ||p); Total Variation, TV(πθ||p); and Jensen-Shannon, JS(πθ||p). We use importance sampling to estimate these divergences.

 

2. KL(πθ||a), a measure of the divergence from original LM a (Ziegler et al., 2019; Khalifa et al., 2021).

 

3. Alignment score, measured by moments Ex∼πθ ϕ(x) of a feature of interest ϕ(x).

 

4. Normalized Entropy (Berger et al., 1996), a measure of diversity in probability distribution normalized by number of tokens. 5. Standard deviation of a minibatch’s pseudo-rewards, std(rθ(x)), where rθ is defined as in Sec. 3.3.

---

4.1. Alignment with Scalar Preferences

Task

We begin with the task of maximizing a scalar preference with KL penalties, whose target distribution, pRLKL, is defined in Eq. 3. We set r(x) = log ϕ(x) where ϕ(x) is the probability returned by a sentiment classifier finetuned from Distil-BERT (HF Canonical Model Maintainers, 2022). This reward function is optimal for modeling a decision-maker which given k different samples x1, . . . , xk, will pick xi with probability proportional to ϕ(xi) (see Appendix F). We set β = 0.1, which is in line with the range of values explored by Ziegler et al. (2019). Note that applying RKL-DPG on pRLKL is equivalent to the RL with KL penalties method, as described in Sec. 3.4. However, through f-DPG we can explore alternative objectives to approximate the same target.

Results

Fig. 2 shows the evolution of the above-mentioned metrics. Further details are given in Fig. 11 in the Appendix. We observe that whereas RKL-DPG achieves by far the best performance in terms of reverse KL, KL(πθ||p) (top-right), it fails to minimize all other divergence metrics. This shows that minimizing one divergence does not necessarily imply that other divergences will follow. Notably, RKL-DPG yields the highest value of alignment score Eπθ [ϕ(x)] at the cost of a significant departure from a. We connect this to the strong influence that low values p(x) have on RKL-DPG, which induces a large pseudo-reward for strongly reducing πθ(x) on those samples (see Sec 5) and produces the spike at the beginning of training in std(rewards). This can lead πθ(x) to concentrate on high-probability regions of p(x), at the cost of diversity, which can also be seen in the low entropy of the generated samples. Interestingly, the three remaining variants of DPG (KL, TV and JS) consistently minimize all four tracked divergences, with JS-DPG performing best overall.

 

In App. D.1, we show additional metrics on generated sentences, which show low diversity but high quality for RKL-DPG, compared to other f-DPGs, suggesting it captures a subset of the target distribution (“mode collapse”), as commonly observed in other generative models (Huszar, 2015; Che et al., 2017; Mescheder et al., 2018).

---

4.2. Alignment with Lexical Constraints

Task

In this task, we constrain the presence of a specific word in the generated text. Following Khalifa et al. (2021), we formulate this goal as a binary preference on the LM by using a target distribution pGDC bin, where b(x) = 1 iff the target word appears in the sequence x, and using a scalar preference target distribution pRLKL where r(x) is set in the same way as b(x) above. Note that in the GDC framework, pGDC bin(x) = 0 when b(x) = 0, implying that reverse KL, namely KL(πθ||p), becomes infinite, so RKL-DPG cannot be used (nor measured) for that target. We use four words with different occurrence frequency: “amazing”(1· 10^−3 ), “restaurant” (6· 10^−4 ), “amusing” (6· 10^−5 ), and “Wikileaks” (8· 10^−6 ).

Results

The aggregated evolution of the metrics for both GDC and RL with KL penalties framework is presented in Fig. 3 (Fig. 1 shows a simplified view of Fig. 3 (a)). Disaggregated results for each task are presented on App. G. We see that all variants of f-DPG reduce the divergence from the target distribution across all measured f-divergences. Furthermore, as expected, convergence to the target is connected with the success ratio in producing the desired word, Eπθ [b(x)], while balancing it with a moderate divergence from a, KL(πθ||a). This reflects that approaching the optimal distribution p translates into metrics in the downstream task. Strinklingly, the original KL-DPG is outperformed by all other variants of f-DPG, even in terms of forward KL. We hypothesize that this is linked to the high variance of the pseudo-rewards in KL-DPG, as visualized in the last panel of Fig. 3 (a) and (b). In Sec. 5, we suggest an interpretation for this. We also observe that RKL-DPG tends to produce distributions with lower normalized entropy. Despite this effect, we found no significant difference in diversity among the generated sentences (see Tab. 4 in App. D.1)

---

4.3. Alignment with Distributional Constraints

Task

We now investigate enforcing distributional preferences on the LM. We focus on debiasing the pretrained model on two kinds of preferences, namely genders’ prevalence (Khalifa et al., 2021) and regard relative to religious groups. The preferences for the genders’ debiasing task are defined as ϕ1(x) = 1 iff x contains more female than male pronouns, with desired moment µ¯1 = 0.5 and ϕ2(x) = 1 iff x contains at least one of the words in the ‘science’ word list compiled by Dathathri et al. (2020), with desired moment µ¯2 = 1. For regard debiasing, we use a single distributional constraint where 0 < ϕ(x) < 1 is a regard score of the sentence when prompted with Muslims, evaluated with a pretrained classifier (Sheng et al., 2019). We set the desired moment µ¯ = 0.568, the regard score observed Christians. The initial average regard score given Muslims is 0.385. For the first experiment, we use GPT-2 small as the initial model a, additionally fine-tuned on the WikiBio dataset (Lebret et al., 2016), whereas for the last one we use vanilla GPT-2 small.

Results

We report the results of both experiments on Fig. 4. For the regard score rebalancing, we considerably reduce bias in the regard score for two different demographic groups, from initial regard score ratio E [ϕ(x)| Christians] : E [ϕ(x)| Muslims] = 1 : 0.677 to E [ϕ(x)| Christians] : E [ϕ(x)| Muslims] = 1 : 0.801 on average. Interestingly, this task showcases a weakness of TV-DPG: Because the original distribution is already close to the target, the hard-thresholded pseudo-reward has a large variance (last panel of Fig 4(b)), inducing noisy gradient estimates and, consequently, sub-optimal convergence. Concerning the gender debiasing experiments, we can see that all other variants of f-DPG outperform the original KL-DPG explored in Khalifa et al. (2021), with RKL-DPG giving the best results and better matching the pointwise constraint although seemingly at the cost of lower diversity as measured by the entropy.

---

4.4. Alignment with Conditional Constraints

Task

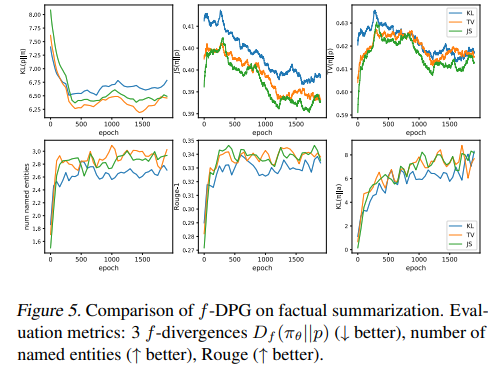
We adopt the conditional task from Korbak et al. (2022a), which aims to constrain the T5 (Raffel et al., 2020) language model to generate more factually faithful summaries (Maynez et al., 2020; Nan et al., 2021). Specifically, let NER(·) denote the set of named entities found in a text. Then, b(x, c) = 1 iff [NER(x) ⊆ NER(c)] ∧ [|NER(x)| ≥ 4], and 0 otherwise. Following the authors, we sample source documents from the the CNN/Daily Mail dataset (Nallapati et al., 2016), i.e. τ (c) is a uniform distribution over a given subset of source documents. In addition to the divergences, we evaluate the performance using Rouge (Lin, 2004), a measure of summarization quality in terms of unigram overlap between the source document and ground truth summary (See App. E for additional metrics and more experiments on code generation with compilability preferences).

Results

We present the evolution of metrics in Fig. 5. The results show that f-DPG increases the fraction of consistent named entities in summarization, and interestingly, this also leads to indirect improvement in the overall quality of generated summaries compared to ground truth, even though ground truth summaries are not used in training. As also observed in Sec. 4.2, JS-DPG leads to better convergence to p than KL-DPG as used in Korbak et al. (2022a).

---

4.5. Scaling Trends of f-DPG

We conduct experiments to investigate the effect of model size on our approach using the scalar preference task described in Sec. 4.1. Specifically, we gradually increase the model size from GPT-2 “small” (117M parameters) to “xl” (1.5B parameters) while tracking two important metrics: alignment score, which is measured by the expected reward Eπθ [ϕ(x)], and diversity, which is measured by the entropy. Figure 6 demonstrates that the alignment score steadily improves as the model size increases. However, we observe persistent differences between the divergence objectives for different f-DPGs, leaving the general order between f-DPGs intact with increasing model size (See Fig. 16 in App. G for evolution of metrics through training epochs). The scaling trend of LM alignment, characterized by a gradual and predictable increase without sudden shifts in performance, aligns with previous findings in the literature (Bai et al., 2022a). Nonetheless, our study further emphasizes the importance of proper divergence objectives, as increasing model size alone does not necessarily bridge the gap between optimal and suboptimal objectives. The smooth and gradual increase of the alignment score as a function of model size suggests that our findings will generalize to even larger LMs.

---

4.6. Ablation Study

This section presents just the key findings of our study. Full results and detailed discussions can be found in App. H.

Effect of parameter family capacity

All experiments presented so far correspond to possibly mis-specified target distributions. To understand whether the observed behavior of different variants f-DPG is affected by this factor, we used pre-trained models with the same architecture as πθ and p. We found that KL-DPG again lags considerably in terms of divergence, while presenting a high variance of in the pseudo-reward. RKL-DPG shows a significant drop of entropy in the initial phase, but with full capacity of parameter family, the model can recover, and cover the rest of the distribution. Additionally, applying zero-shot the fine-tuned LMs to a summarization task, following Radford et al. (2019), we found that the they recover to a large extent the quality of the target distribution.

Effect of training scheme

We examined different training schemes for the lexical constraint on “amazing” from Sec. 4.2. We saw that the use of a baseline technique improves the performance of the f-DPG method, with RKLDPG showing the greatest benefit. Additionally, we found that even though a large batch size is effective at reducing the variance of KL-DPG, we still observe KL-DPG to perform comparatively worse than other divergences. Finally, we observe that our importance sampling estimates converged to the true value of Z.

---

5. Discussion and Conclusion

 

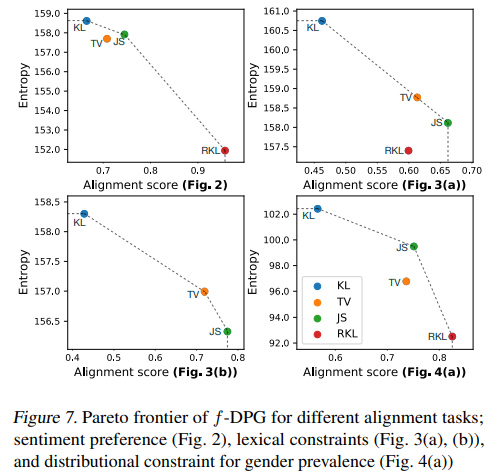
A plausible hypothesis would have been that each variant of f-DPG is comparatively better at least in terms of the f-divergence objective being optimized. Surprisingly, we found that, save for a few exceptions (Sec. 4.1), for a given target there is one or a few variants that are the best across all measured divergences. Furthermore, we observed that divergence measures can have a significant impact on the performance of the model depending on the target distribution. Fig. 7 summarizes the Pareto frontier of the alignment-diversity trade-off of the f-DPG method. The results demonstrate that RKL-DPG and KL-DPG consistently represent two contrasting extremes: RKL-DPG shows high alignment but limited diversity, whereas KL-DPG exhibits low alignment but high diversity. JS-DPG shows a balanced trade-off between alignment and diversity and consistently appeared on the Pareto frontier across all experiments we conducted.

 

Fig. 8 illustrates the differences between pseudo-rewards for distinct f-divergences, giving a plausible explanation for the observed differences. The forward KL loss aims to ensure coverage of the subset where p(x) > 0, giving a large pseudo-reward for samples with p(x)>>π(x). However, the optimization can be sensitive to sampling noise in the finite sample approximation (see, e.g., Sec. 4.2). Conversely, the reverse KL loss results in extreme negative rewards for samples with p(x)<<πθ(x), leading πθ to avoid such regions and resulting in distributional collapse (Sec. 4.1). Total Variation loss is robust to outliers thanks to its hard-thresholded pseudo-reward, however it can lead to high variance behavior when πθ ≈ p (Sec. 4.3). On the other hand, the Jensen-Shannon loss gives smooth and robust rewards in both directions and prevents πθ from heavily relying on a single direction, making it a reasonable default choice as confirmed by our experiments.

그래서 결국 왜 이런 실험 결과가 나온건지에 대해서 좀 더 생각해 봐야 함.

To conclude, we propose a flexible framework for approximating a target distribution by minimizing any f-divergence, unifying earlier approaches for aligning language models. Our results on a diverse array of tasks show that minimizing well-chosen f-divergences leads to significant gains over previous work. The fact that increasing the model size improves the alignment score but does not inherently bridge the gap between objectives underscores the importance of selecting appropriate divergence objectives.

---

A. Complements on Formal Aspects and Proofs

A.1. Equivalent definitions for f-divergences

The definition of f-divergences of Eq. 6 is equivalent to a second definition, in a more “symmetrical” format, following (Liese & Vajda, 2006), which will help in some derivations, in particular in the proof of Theorem 1.

---

A.2. Illustrations of a few f-divergences

Let’s now see how the notion of f-divergence can be applied to a few common cases.

---

A.3. Proof of Theorem 1

---

 

A.5. f-DPG algorithm

 

---

B. Extended Related Work

RL for LMs

There is a large reinforcement learning inspired literature about steering an autoregressive sequential model towards optimizing some global reward over the generated text. This includes REINFORCE (Williams, 1992) for Machine Translation (Ranzato et al., 2016), actor critic for Abstractive Summarization (Paulus et al., 2018), Image-to-Text (Liu et al., 2016), Dialogue Generation (Li et al., 2016b), and Video Captioning (Pasunuru & Bansal, 2017). With respect to rewards, some approaches for Machine Translation and Summarization (Ranzato et al., 2016; Bahdanau et al., 2017) directly optimize end task rewards such as BLEU and ROUGE at training time to compensate for the mismatch between the perplexity-based training of the initial model and the evaluation metrics used at test time. Some others use heuristic rewards as in (Li et al., 2016b; Tambwekar et al., 2019), in order to improve certain a priori desirable features of generated stories or dialogues.

 

Several studies, have considered incorporating a distributional term inside the reward to be maximized. In particular Jaques et al. (2017; 2019); Ziegler et al. (2019); Stiennon et al. (2020) have applied variations of KL-control (Todorov, 2006b; Kappen et al., 2013) which adds a penalty term to the reward term so that the resulting policy does not deviate too much from the original one in terms of KL-divergence. The overall objective with the KL-penalty is maximized using an RL algorithm of choice including: PPO (Schulman et al., 2017) as in Ziegler et al. (2019) or Q-learning (Mnih et al., 2013) as in Jaques et al. (2017). This approach recently get a huge attention with its impact with using the human data to train aligned language models in LaMDA (Thoppilan et al., 2022), InstructGPT (Ouyang et al., 2022), Sparrow (Glaese et al., 2022), and CAI (Bai et al., 2022b). Similar work involving model self-critique and natural language feedback includes (Zhao et al., 2021; Scheurer et al., 2022; Saunders et al., 2022)

f-divergence objectives for generative models

In the literature, there have been several studies exploring the use of f-divergences in generative models. Goodfellow et al. (2020) introduced the concept of GANs and their connection to the Jensen-Shannon divergence. Nowozin et al. (2016) proposed a variational expression of f-divergences as a loss function for GANs. Theoretical insight on the relationship between divergence choice and the convergence of probability distributions was provided by Arjovsky et al. (2017). Additionally, Theis et al. (2016) discussed potential drawbacks of forward KL divergence in generative models and Huszar (2015) proposed a generalization of Jensen-Shannon divergence that interpolates between KL and reverse KL and has Jensen-Shannon as its midpoint.

 

The connections between RL and divergence minimization have also been explored, with studies showing that entropy regularization in RL can be viewed as minimizing reverse KL divergence between reward-weighted trajectory and policy trajectory distributions (Kappen et al., 2013; Levine, 2018). Other studies have also explored the use of forward KL divergence in RL (Peters & Schaal, 2007; Norouzi et al., 2016). Additionally, a unified probabilistic perspective on f-divergence minimization in imitation learning has been presented for both discrete and continuous control environments (Ke et al., 2021; Ghasemipour et al., 2020).

 

Wang et al. (2018) introduced variational inference with adaptive f-divergences and demonstrated its effectiveness in RL, with focus on continuous sample spaces. Their Proposition 4.2.1 is similar to our theorem 1. However, our result exhibits greater generality by defining Df (πθ||p) without requirements of absolute continuity in either direction (Polyanskiy, 2019; Liese & Vajda, 2006). We note that this generalization is crucial for LM alignment, as the case of p(x) = 0, πθ(x) > 0 can easily occur.

---