1. Motivation: Why You Might Care

https://www.bradyneal.com/causal-inference-course#course-textbook

---

1.1. Simpson's Paradox

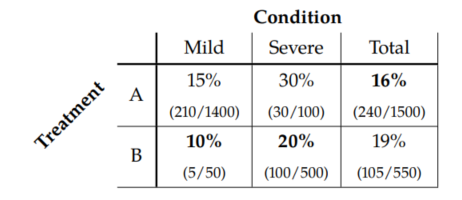
A key ingredient necessary to find Simpson's paradox is the non-uniformity of allocation of people to the groups. 

Scenario 1

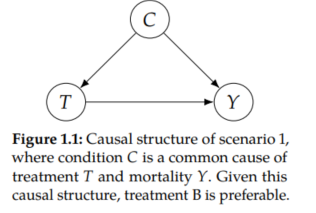
If the condition C is a cause of the treatment T, treatment B is more effective at reducing mortality Y. Because having severe condition causes one to be more likely to die (C → Y) and causes one to be more likely to receive treatment B (C → T), treatment B will be associated with higher mortality in the total population.

 

Treatment B is associated with a higher mortality rate simply because condition is a common cause of both treatment and mortality. Condition confounds the effect of treatment on mortality. To correct for this confounding, we must examine the relationship of T and Y among patients with the same conditions. This means that the better treatment is the one that yields lower mortality in each of the subpopulations: treatment B.

Scenario 2

If the prescription of treatment T is a cause of the condition C, treatment A is more effective. An example scenario is where treatment B is so scarse that it requires patients to wait a long time after they were prescribed the treatment before they can receive the treatment. Treatment A does not have this problem. Because the condition of a patient with COVID-27 worsens over time, the prescription of treatment B actually causes patients with mild conditions to develop severe conditions, causing a higher mortality rate. Therefore, even if treatment B is more effective than treatment A once administered (positive effect along T → Y), because prescription of treatment B causes worse conditions (negative effect along T → C → Y), treatment B is less effective in total. 

 

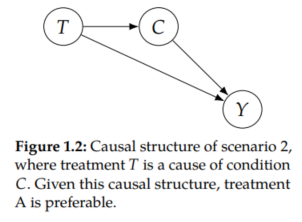
In sum, the more effective treatment is completely dependent on the causal structure of the problem. In Scenario 1, where C was a cause of T, treatment B was more effective. In Scenario 2, where T was a cause of C, treatment A was more effective. Without causality, Simpson's paradox cannot be resolved. With causality, it is not a paradox at all.

---

1.2. Applications of Causal Inference

Causal inference is essential to science, as we often want to make causal claims, rather than merely associational claims. For example, if we are choosing between treatments for a disease, we want to choose the treatment that causes the most people to be cured, without causing too many bad side effects. If we want a reinforcement learning algorithm to maximize reward, we want it to take actions that cause it to achieve the maximum reward. If we are studying the effect of social media on mental health, we are trying to understand what the main causes of a given mental health outcome are and order these causes by the percentage of the outcome that can be attributed to each cause.

 

Causal inference is essential for rigorous decision-making. For example, say we are considering several different policies to implement to reduce greenhouse gas emissions, and we must choose just one due to budget constraints. If we want to be maximally effective, we should carry out causal analysis to determine which policy will cause the largest reduction in emissions. As another example, say we are considering several interventions to reduce global poverty. We want to know which policies will cause the largest reductions in poverty.

 

Now that we've gone through the general example of Simpson's paradox and a few specific examples in science and decision-making, we'll move to how causal inference is so different from prediction.

---

1.3. Correlation Does Not Imply Causation

Why is Association Not Causation?

"correlation" is technically only a measure of linear statistical dependence. We will largely be using the term association to refer to statistical dependence from now on.

 

For any given amount of association, it does not need to be "all of the association is causal" or "none of the association is causal." Rather, it is possible to have a large amount of association with only some of it being causal. 

 

The phrase "association is not causation" simply means that the amount of association and the amount of causation can be different.

 

We can explain how wearing shoes to bed and headaches are associated without either being a cause of the other. It turns out that they are both caused by a common cause: drinking the night before. You might also hear this kind of variable referred to as a "confounder" or a "lurking variable." We will call this kind of association "confounding association", since the association is facilitated by a confounder.

 

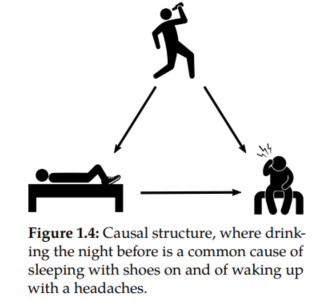
The total association observed can be made up of both confounding association and causal association.

 

The main problem motivating causal inference is that association is not causation. As we'll see in Chapter 5, if we randomly assign the treatment in a controlled experiment, association actually is causation.

---

1.4. Main Themes

Statistical vs. Causal 

Even with an infinite amount of data, we sometimes cannot compute some causal quantities. In contrast, much of statistics is about addressing uncertainty in finite samples. When given infinite data, there is no uncertainty. 

 

However, association, a statistical concept, is not causation. There is more work to be done in causal inference, even after starting with infinite data. This is the main distinction motivating causal inference. We have already made this distinction in this chapter and will continue to make this distinction throughout the book.

Identification vs. Estimation

Identification of causal effects is unique to causal inference. It is the problem that remains to solve, even when we have infinite data. However, causal inference also shares estimation with traditional statistics and machine learning. We will largely begin with identification of causal effects (in Chapters 2, 4, and 6) before moving to estimation of causal effects (in Chapter 7). 

Interventional vs. Observational

If we can intervene/experiment, identification of causal effects is relatively easy. This is simply because we can actually take the action that we want to measure the causal effect of and simply measure the effect after we take that action. Observational data is where it gets more complicated because confounding is almost always introduced into the data. 

Assumptions

There will be a large focus on what assumptions we are using to get the results that we get. Clear assumptions should make it easy to see where critiques of a given causal analysis or causal model will be. The hope is that presenting assumptions clearly will lead to more lucid discussions about causality.

---