[Factor VAE] Disentangling by Factorising

KL Decomposition

 

---

Mutual Information

---

※ https://arxiv.org/pdf/1802.05983.pdf

Abstract

We define and address the problem of unsupervised learning of disentangled representations on data generated from independent factors of variation. We propose FactorVAE, a method that disentangles by encouraging the distribution of representations to be factorial and hence independent across the dimensions. We show that it improves upon β-VAE by providing a better trade-off between disentanglement and reconstruction quality. Moreover, we highlight the problems of a commonly used disentanglement metric and introduce a new metric that does not suffer from them.

---

1. Introduction

Learning interpretable representations of data that expose semantic meaning has important consequences for artificial intelligence. Such representations are useful not only for standard downstream tasks such as supervised learning and reinforcement learning, but also for tasks such as transfer learning and zero-shot learning where humans excel but machines struggle (Lake et al., 2016). There have been multiple efforts in the deep learning community towards learning factors of variation in the data, commonly referred to as learning a disentangled representation. While there is no canonical definition for this term, we adopt the one due to Bengio et al. (2013): a representation where a change in one dimension corresponds to a change in one factor of variation, while being relatively invariant to changes in other factors. In particular, we assume that the data has been generated from a fixed number of independent factors of variation. We focus on image data, where the effect of factors of variation is easy to visualise.

 

Using generative models has shown great promise in learning disentangled representations in images. Notably, semi-supervised approaches that require implicit or explicit knowledge about the true underlying factors of the data have excelled at disentangling (Kulkarni et al., 2015; Kingma et al., 2014; Reed et al., 2014; Siddharth et al., 2017; Hinton et al., 2011; Mathieu et al., 2016; Goroshin et al., 2015; Hsu et al., 2017; Denton & Birodkar, 2017). However, ideally we would like to learn these in an unsupervised manner, due to the following reasons: 1. Humans are able to learn factors of variation unsupervised (Perry et al., 2010). 2. Labels are costly as obtaining them requires a human in the loop. 3. Labels assigned by humans might be inconsistent or leave out the factors that are difficult for humans to identify.

 

β-VAE (Higgins et al., 2016) is a popular method for unsupervised disentangling based on the Variational Autoencoder (VAE) framework (Kingma & Welling, 2014; Rezende et al., 2014) for generative modelling. It uses a modified version of the VAE objective with a larger weight (β > 1) on the KL divergence between the variational posterior and the prior, and has proven to be an effective and stable method for disentangling. One drawback of β-VAE is that reconstruction quality (compared to VAE) must be sacrificed in order to obtain better disentangling. The goal of our work is to obtain a better trade-off between disentanglement and reconstruction, allowing to achieve better disentanglement without degrading reconstruction quality. In this work, we analyse the source of this trade-off and propose FactorVAE, which augments the VAE objective with a penalty that encourages the marginal distribution of representations to be factorial without substantially affecting the quality of reconstructions. This penalty is expressed as a KL divergence between this marginal distribution and the product of its marginals, and is optimised using a discriminator network following the divergence minimisation view of GANs (Nowozin et al., 2016; Mohamed & Lakshminarayanan, 2016). Our experimental results show that this approach achieves better disentanglement than β-VAE for the same reconstruction quality. We also point out the weaknesses in the disentangling metric of Higgins et al. (2016), and propose a new metric that addresses these shortcomings.

 

A popular alternative to β-VAE is InfoGAN (Chen et al., 2016), which is based on the Generative Adversarial Net (GAN) framework (Goodfellow et al., 2014) for generative modelling. InfoGAN learns disentangled representations by rewarding the mutual information between the observations and a subset of latents. However at least in part due to its training stability issues (Higgins et al., 2016), there has been little empirical comparison between VAE-based methods and InfoGAN. Taking advantage of the recent developments in the GAN literature that help stabilise training, we include InfoWGAN-GP, a version of InfoGAN that uses Wasserstein distance (Arjovsky et al., 2017) and gradient penalty (Gulrajani et al., 2017), in our experimental evaluation.

 

In summary, we make the following contributions: 1) We introduce FactorVAE, a method for disentangling that gives higher disentanglement scores than β-VAE for the same reconstruction quality. 2) We identify the weaknesses of the disentanglement metric of Higgins et al. (2016) and propose a more robust alternative. 3) We give quantitative comparisons of FactorVAE and β-VAE against InfoGAN’s WGAN-GP counterpart for disentanglement.

---

2. Trade-off between Disentanglement and Reconstruction in β-VAE

We motivate our approach by analysing where the disentanglement and reconstruction trade-off arises in the βVAE objective. First, we introduce notation and architecture of our VAE framework. We assume that observations x (i) ∈ X , i = 1, . . . , N are generated by combining K underlying factors f = (f1, . . . , fK). These observations are modelled using a real-valued latent/code vector z ∈ R d , interpreted as the representation of the data. The generative model is defined by the standard Gaussian prior p(z) = N (0, I), intentionally chosen to be a factorised distribution, and the decoder pθ(x|z) parameterised by a neural net. The variational posterior for an observation is

 

, with the mean and variance produced by the encoder, also parameterised by a neural net. The variational posterior can be seen as the distribution of the representation corresponding to the data point x. The distribution of representations for the entire data set is then given by

which is known as the marginal posterior or aggregate posterior, where pdata is the empirical data distribution. A disentangled representation would have each zj correspond to precisely one underlying factor fk. Since we assume that these factors vary independently, we wish for a factorial distribution

 

The β-VAE objective

is a variational lower bound on

 

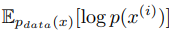
for β ≥ 1, reducing to the VAE objective for β = 1. Its first term can be interpreted as the negative reconstruction error, and the second term as the complexity penalty that acts as a regulariser. We may further break down this KL term as (Hoffman & Johnson, 2016; Makhzani & Frey, 2017)

 

where I(x; z) is the mutual information between x and z under the joint distribution pdata(x)q(z|x). See Appendix C for the derivation. Penalising the KL(q(z)||p(z)) term pushes q(z) towards the factorial prior p(z), encouraging independence in the dimensions of z and thus disentangling. Penalising I(x; z), on the other hand, reduces the amount of information about x stored in z, which can lead to poor reconstructions for high values of β (Makhzani & Frey, 2017). Thus making β larger than 1, penalising both terms more, leads to better disentanglement but reduces reconstruction quality. When this reduction is severe, there is insufficient information about the observation in the latents, making it impossible to recover the true factors. Therefore there exists a value of β > 1 that gives highest disentanglement, but results in a higher reconstruction error than a VAE.

---

3. Total Correlation Penalty and FactorVAE

Penalizing I(x; z) more than a VAE does might be neither necessary nor desirable for disentangling. For example, InfoGAN disentangles by encouraging I(x; c) to be high where c is a subset of the latent variables z. Hence we motivate FactorVAE by augmenting the VAE objective with a term that directly encourages independence in the code distribution, arriving at the following objective:

 

where

 

Note that this is also a lower bound on the marginal log likelihood Epdata(x) [log p(x)]. KL(q(z)||q¯(z)) is known as Total Correlation (TC, Watanabe, 1960), a popular measure of dependence for multiple random variables. In our case this term is intractable since both q(z) and q¯(z) involve mixtures with a large number of components, and the direct Monte Carlo estimate requires a pass through the entire data set for each q(z) evaluation. Hence we take an alternative approach for optimizing this term. We start by observing we can sample from q(z) efficiently by first choosing a datapoint x (i) uniformly at random and then sampling from q(z|x (i) ). We can also sample from q¯(z) by generating d samples from q(z) and then ignoring all but one dimension for each sample. A more efficient alternative involves sampling a batch from q(z) and then randomly permuting across the batch for each latent dimension (see Alg. 1). This is a standard trick used in the independence testing literature (Arcones & Gine, 1992) and as long as the batch is large enough, the distribution of these samples will closely approximate q¯(z).

 

Having access to samples from both distributions allows us to minimise their KL divergence using the density-ratio trick (Nguyen et al., 2010; Sugiyama et al., 2012) which involves training a classifier/discriminator to approximate the density ratio that arises in the KL term. Suppose we have a discriminator D (in our case an MLP) that outputs an estimate of the probability D(z) that its input is a sample from q(z) rather than from q¯(z). Then we have

 

We train the discriminator and the VAE jointly. In particular, the VAE parameters are updated using the objective in Eqn. (2), with the TC term replaced using the discriminator based approximation from Eqn. (3). The discriminator is trained to classify between samples from q(z) and q¯(z), thus learning to approximate the density ratio needed for estimating TC. See Alg. 2 for pseudocode of FactorVAE.

 

It is important to note that low TC is necessary but not sufficient for meaningful disentangling. For example, when q(z|x) = p(z), TC=0 but z carries no information about the data. Thus having low TC is only meaningful when we can preserve information in the latents, which is why controlling for reconstruction error is important.

 

In the GAN literature, divergence minimisation is usually done between two distributions over the data space, which is often very high dimensional (e.g. images). As a result, the two distributions often have disjoint support, making training unstable, especially when the discriminator is strong. Hence it is necessary to use tricks to weaken the discriminator such as instance noise (Sønderby et al., 2016) or to replace the discriminator with a critic, as in Wasserstein GANs (Arjovsky et al., 2017). In this work, we minimise divergence between two distributions over the latent space (as in e.g. (Mescheder et al., 2017)), which is typically much lower dimensional and the two distributions have overlapping support. We observe that training is stable for sufficiently large batch sizes (e.g. 64 worked well for d = 10), allowing us to use a strong discriminator.

---

7. Conclusion and Discussion

We have introduced FactorVAE, a novel method for disentangling that achieves better disentanglement scores than β-VAE on the 2D Shapes and 3D Shapes data sets for the same reconstruction quality. Moreover, we have identified weaknesses of the commonly used disentanglement metric of Higgins et al. (2016), and proposed an alternative metric that is conceptually simpler, is free of hyperparameters, and avoids the failure mode of the former. Finally, we have performed an experimental evaluation of disentangling for the VAE-based methods and InfoWGAN-GP, a more stable variant of InfoGAN, and identified its weaknesses relative to the VAE-based methods.

 

One of f the limitations of our approach is that low Total Correlation is necessary but not sufficient for disentangling of independent factors of variation. For example, if all but one of the latent dimensions were to collapse to the prior, the TC would be 0 but the representation would not be disentangled. Our disentanglement metric also requires us to be able to generate samples holding one factor fixed, which may not always be possible, for example when our training set does not cover all possible combinations of factors. The metric is also unsuitable for data with nonindependent factors of variation.

 

For future work, we would like to use discrete latent variables to model discrete factors of variation and investigate how to reliably capture combinations of discrete and continuous factors using discrete and continuous latents.