[IWAE] Importance Weighted Autoencoders

※ https://arxiv.org/pdf/1509.00519.pdf

---

Abstract

The variational autoencoder (VAE; Kingma & Welling (2014)) is a recently proposed generative model pairing a top-down generative network with a bottom-up recognition network which approximates posterior inference. It typically makes strong assumptions about posterior inference, for instance that the posterior distribution is approximately factorial, and that its parameters can be approximated with nonlinear regression from the observations. As we show empirically, the VAE objective can lead to overly simplified representations which fail to use the network’s entire modeling capacity. We present the importance weighted autoencoder (IWAE), a generative model with the same architecture as the VAE, but which uses a strictly tighter log-likelihood lower bound derived from importance weighting. In the IWAE, the recognition network uses multiple samples to approximate the posterior, giving it increased flexibility to model complex posteriors which do not fit the VAE modeling assumptions. We show empirically that IWAEs learn richer latent space representations than VAEs, leading to improved test log-likelihood on density estimation benchmarks.

---

1. Introduction

In recent years, there has been a renewed focus on learning deep generative models (Hinton et al., 2006; Salakhutdinov & E., 2009; Gregor et al., 2014; Kingma & Welling, 2014; Rezende et al., 2014). A common difficulty faced by most approaches is the need to perform posterior inference during training: the log-likelihood gradients for most latent variable models are defined in terms of posterior statistics (e.g. Salakhutdinov & E. (2009); Neal (1992); Gregor et al. (2014)). One approach for dealing with this problem is to train a recognition network alongside the generative model (Dayan et al., 1995). The recognition network aims to predict the posterior distribution over latent variables given the observations, and can often generate a rough approximation much more quickly than generic inference algorithms such as MCMC.

 

The variational autoencoder (VAE; Kingma & Welling (2014); Rezende et al. (2014)) is a recently proposed generative model which pairs a top-down generative network with a bottom-up recognition network. Both networks are jointly trained to maximize a variational lower bound on the data loglikelihood. VAEs have recently been successful at separating style and content (Kingma et al., 2014; Kulkarni et al., 2015) and at learning to “draw” images in a realistic manner (Gregor et al., 2015).

 

VAEs make strong assumptions about the posterior distribution. Typically VAE models assume that the posterior is approximately factorial, and that its parameters can be predicted from the observables through a nonlinear regression. Because they are trained to maximize a variational lower bound on the log-likelihood, they are encouraged to learn representations where these assumptions are satisfied, i.e. where the posterior is approximately factorial and predictable with a neural network. While this effect is beneficial, it comes at a cost: constraining the form of the posterior limits the expressive power of the model. This is especially true of the VAE objective, which harshly penalizes approximate posterior samples which are unlikely to explain the data, even if the recognition network puts much of its probability mass on good explanations.

 

In this paper, we introduce the importance weighted autoencoder (IWAE), a generative model which shares the VAE architecture, but which is trained with a tighter log-likelihood lower bound derived from importance weighting. The recognition network generates multiple approximate posterior samples, and their weights are averaged. As the number of samples is increased, the lower bound approaches the true log-likelihood. The use of multiple samples gives the IWAE additional flexibility to learn generative models whose posterior distributions do not fit the VAE modeling assumptions. This approach is related to reweighted wake sleep (Bornschein & Bengio, 2015), but the IWAE is trained using a single unified objective. Compared with the VAE, our IWAE is able to learn richer representations with more latent dimensions, which translates into significantly higher log-likelihoods on density estimation benchmarks.

---

2. Background

In this section, we review the variational autoencoder (VAE) model of Kingma & Welling (2014). In particular, we describe a generalization of the architecture to multiple stochastic hidden layers. We note, however, that Kingma & Welling (2014) used a single stochastic hidden layer, and there are other sensible generalizations to multiple layers, such as the one presented by Rezende et al. (2014).

 

The VAE defines a generative process in terms of ancestral sampling through a cascade of hidden layers:

Here, θ is a vector of parameters of the variational autoencoder, and

denotes the stochastic hidden units, or latent variables. The dependence on θ is often suppressed for clarity. For convenience, we define h0 = x.

Each of the terms

may denote a complicated nonlinear relationship, for instance one computed by a multilayer neural network.

However, it is assumed that sampling and probability evaluation are tractable for each

Note that L denotes the number of stochastic hidden layers; the deterministic layers are not shown explicitly here. We assume the recognition model q(h|x) is defined in terms of an analogous factorization:

where sampling and probability evaluation are tractable for each of the terms in the product.

 

In this work, we assume the same families of conditional probability distributions as Kingma & Welling (2014). In particular, the prior p(h L) is fixed to be a zero-mean, unit-variance Gaussian. In general, each of the conditional distributions p(h l | h l+1) and q(h l |h l−1) is a Gaussian with diagonal covariance, where the mean and covariance parameters are computed by a deterministic feed-forward neural network. For real-valued observations, p(x|h 1) is also defined to be such a Gaussian; for binary observations, it is defined to be a Bernoulli distribution whose mean parameters are computed by a neural network.

 

The VAE is trained to maximize a variational lower bound on the log-likelihood, as derived from Jensen’s Inequality:

 

Since L(x) = log p(x) − DKL(q(h|x)||p(h|x)), the training procedure is forced to trade off the data log-likelihood log p(x) and the KL divergence from the true posterior. This is beneficial, in that it encourages the model to learn a representation where posterior inference is easy to approximate.

 

If one computes the log-likelihood gradient for the recognition network directly from Eqn. 3, the result is a REINFORCE-like update rule which trains slowly because it does not use the log-likelihood gradients with respect to latent variables (Dayan et al., 1995; Mnih & Gregor, 2014). Instead, Kingma & Welling (2014) proposed a reparameterization of the recognition distribution in terms of auxiliary variables with fixed distributions, such that the samples from the recognition model are a deterministic function of the inputs and auxiliary variables. While they presented the reparameterization trick for a variety of distributions, for convenience we discuss the special case of Gaussians, since that is all we require in this work. (The general reparameterization trick can be used with our IWAE as well.)

 

In this paper, the recognition distribution q(h l |h l−1 , θ) always takes the form of a Gaussian

 

whose mean and covariance are computed from the the states of the hidden units at the previous layer and the model parameters. This can be alternatively expressed by first sampling an auxiliary variable

and then applying the deterministic mapping

 

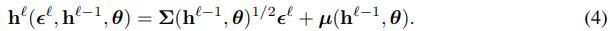
The joint recognition distribution q(h|x, θ) over all latent variables can be expressed in terms of a deterministic mapping h(e, x, θ), with e = (e 1 , . . . , e L), by applying Eqn. 4 for each layer in sequence. Since the distribution of e does not depend on θ, we can reformulate the gradient of the bound L(x) from Eqn. 3 by pushing the gradient operator inside the expectation:

 

Assuming the mapping h is represented as a deterministic feed-forward neural network, for a fixed e, the gradient inside the expectation can be computed using standard backpropagation. In practice, one approximates the expectation in Eqn. 6 by generating k samples of e and applying the Monte Carlo estimator

with w(x, h, θ) = p(x, h|θ)/q(h|x, θ). This is an unbiased estimate of ∇θL(x). We note that the VAE update and the basic REINFORCE-like update are both unbiased estimators of the same gradient, but the VAE update tends to have lower variance in practice because it makes use of the log-likelihood gradients with respect to the latent variables.

---

3. Importance Weighted Autoencoder

The VAE objective of Eqn. 3 heavily penalizes approximate posterior samples which fail to explain the observations. This places a strong constraint on the model, since the variational assumptions must be approximately satisfied in order to achieve a good lower bound. In particular, the posterior distribution must be approximately factorial and predictable with a feed-forward neural network. This VAE criterion may be too strict; a recognition network which places only a small fraction (e.g. 20%) of its samples in the region of high posterior probability region may still be sufficient for performing accurate inference. If we lower our standards in this way, this may give us additional flexibility to train a generative network whose posterior distributions do not fit the VAE assumptions. This is the motivation behind our proposed algorithm, the Importance Weighted Autoencoder (IWAE).

 

Our IWAE uses the same architecture as the VAE, with both a generative network and a recognition network. The difference is that it is trained to maximize a different lower bound on log p(x). In particular, we use the following lower bound, corresponding to the k-sample importance weighting estimate of the log-likelihood:

 

Here, h1, . . . , hk are sampled independently from the recognition model. The term inside the sum corresponds to the unnormalized importance weights for the joint distribution, which we will denote as wi = p(x, hi)/q(hi |x).

 

This is a lower bound on the marginal log-likelihood, as follows from Jensen’s Inequality and the fact that the average importance weights are an unbiased estimator of p(x):

where the expectations are with respect to q(h|x).

 

It is perhaps unintuitive that importance weighting would be a reasonable estimator in high dimensions. Observe, however, that the special case of k = 1 is equivalent to the standard VAE objective shown in Eqn. 3. Using more samples can only improve the tightness of the bound:

 

The bound Lk can be estimated using the straightforward Monte Carlo estimator, where we generate samples from the recognition network and average the importance weights. One might worry about the variance of this estimator, since importance weighting famously suffers from extremely high variance in cases where the proposal and target distributions are not a good match. However, as our estimator is based on the log of the average importance weights, it does not suffer from high variance. This argument is made more precise in Appendix B.

---

6. Conclusion

In this paper, we presented the importance weighted autoencoder, a variant on the VAE trained by maximizing a tighter log-likelihood lower bound derived from importance weighting. We showed empirically that IWAEs learn richer latent representations and achieve better generative performance than VAEs with equivalent architectures and training time. We believe this method may improve the flexibility of other generative models currently trained with the VAE objective.

---

Proof of Theorm 1.