-
[Lecture 7] (2/2) Function ApproximationResearch/RL_DeepMind 2024. 8. 3. 09:55
https://www.youtube.com/watch?v=ook46h2Jfb4&list=PLqYmG7hTraZDVH599EItlEWsUOsJbAodm&index=7



Now we can't update towards the true value function if we don't have that yet, so instead we're going to substitute the targets.
For Monte Carlo, we could plug in the Monte Carlo return, of course we could also do Temporal Difference learning.
And then we could plug in the Temporal Difference target which is just in the one-step case, it's just the immediate reward plus the discounted value at the next state. So this is now a placeholder for the true value of this state. And we can use that to have data dependent updates where we don't have any hidden information anymore. We don't have any privileged information about the true value of the state.
Of course we can also go in between these with TD lambda.

Now return is an unbiased sample of the true value and therefore we can view this as supervised learning where we have a data set of states and returns.
And then the linear Monte Carlo policy evaluation algorithm which uses that return, but then instead of the gradient has its feature vector will converge to the global optima. This is known because we're trying to find the minimum of a quadratic function which is convex and then stochastic gradient descent with an appropriately decaying step size, we'll find the optimal solution.

We can also consider TD learning. We know that the target here is a biased sample of the true value. But we can apply the same trick where we consider this to be training data where we have states and we have the associated targets for those states and we could update towards those in a very similar way.
This is very similar to Monte Carlo. This is just doing a regression in some sense but using the TD error rather than the Monte Carlo. This is a non-stationary regression problem because we're using the value function itself to construct the targets. That is different from the Monte Carlo case.
The target depends specifically on our parameter. So it's not just any non-stationary regression problem, it's one where we're updating the parameters ourselves and that makes the targets non-stationary. This turns out to be important for the stability of these algorithms.


Policy iteration depends on two steps. One is policy evaluation and the other one is policy improvement.
For policy improvement, if we estimate action value functions, we can use epsilon greedy policy improvement or greey policy improvement, but then you wouldn't explore sufficiently but we can just consider something fairly simple there.
But then the evaluation step is the difficult one if your state space is really large, and therefore we're going to plug in value functions approximation for that step.

So we're going to approximate the value function for the state action pairs in a very similar way as before.
And if we use a linear function, we could define our feature vectors as dependent not just on state but also on action. And then they have the shared parameter vector w which is applied to this feature vector. And then gives you the suitable value estimate. The update is as before.

In linear case, it turns out there's multiple things we could be doing. So a different way to approximate the action value function is as follows where instead of defining a feature vector that depends on state and action, we could have a feature vector that only depends on state. Now the action value function is no longer a scalar function.
Now we have a feature matrix W, and we are going to multiply a feature vector that only depends on state with this feature matrix. And feature matrix is shaped in such a way that the output of this will have the same number of elements as we have actions.
A different way to write down the same thing would be as follows, where we still have this scalar function for state and action, and it's going to be defined as indexing this vector that we get from this first operation with the action.
So we have a matrix that has size number of actions by number of features, so when we multiply that with the number of features, we get a vector of size number of actions, and then we just index in there to get the action value for this action that we're interested in.
This can also be written as follows, where we have a separate parameter function per action, but we have a shared feature vector. Now we have one shared feature vector and separate weights per action.

This raises a question, should we use action-in, where the action is part of your feature representation or action-out, where we just have a state dependent feature representation and then compute all of the action values for all of the different actions.
So the action-in approach is when your feature vector depends on state and action, you have the shared weight vector w. The action-out approach is when you have a weight matrix W and you have features that only depend on state.
One reuses the same weights across actions, the other one reuses the same features across actions.
It's unclear which one is better in general, but they do have some certain other properties. For instance, if we have continuous actions, it does seem easier to have an action-in approach, because you can't have an infinitely large matrix. So the action-out approach seems much more troublesome if you have continous actions.
For small discrete action spaces, the most common approach these days is, action-out.


What the actual optimal policy is, to go left first then start driving down and use the momentum from going down to then drive up the other hill. This is sometimes used because it's a somewhat tricky exploration problem. If you don't know there's any goals to be had or any like rewards to be attained that are non-zero, it could be quite hard for the car to figure out it should leave this ravine at the bottom.
What we see here is, a value function after a number of episodes. We see that the shape of value function changes over time as we add more episodes.
The interesting thing that I want you to look at here is not just the evolution of this value function but also its shape at the end which is quite special. It's not a very simple value function. This is because it depends where you are.
If you're far enough up the hill to the left, then the optimal choice would be to go down and then up the other end. But if you happened to be slightly further down, you're not high up the hill enough yet. Then it could be better to go up further and this also depends on your velecity.
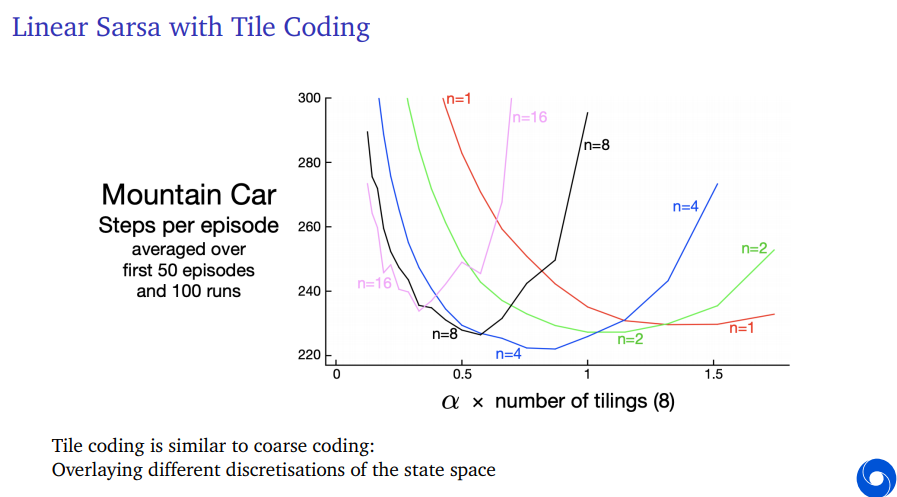
What was the representation here for this mountain car? It's using Tile Coding. There's two inputs. There's the velocity of the agent and it's position. And this was cut up into small little tiles by discretizing them.
No what Tile Coding does so, the simplest version of Tile Coding is, state aggregation. You just cut up the whole space into little squares. This is your feature representation. Alternatively you could also cut it up into larger squares but then have multiple of those overlapping. This is similar to course coding where now instead of being in one of these squares, you could be in multiple squares at the same time.
One such discretization of the space, we could call a tiling of the state space and then Tile Coding could apply multiple tilings that overlap. But they don't exactly overlap, so they're kind of offset from each other, so that you could be in one tile from one tiling but in a different tile from a different tiling.
And then if you have that, you have a feature mapping, you can apply a linear function approximation to this.


When do these algorithms converge? What do we mean with convergence? We mean that they find a solution reliably that they find some sort of a minimum of something.
So do they converge when you bootstrap? When you use function approximation? When you learn Off-policy? It's not always the case. Ideally, we want algorithms that converge in all of those cases or alternatively we want to understand when the algorithms converge and when they do not. So we can avoid cases where they do not.

Let's start with the simplest case which is the Monte Carlo setting. We want to find parameters that minimize the squared error. We're going to call that w_MC for Monte Carlo.
The solution is the expectation of the outer product of your features and that expectation is then inverted, this is an inverse matrix times the expectation of the return times your features. That turns out to be the solution that Monte Carlo finds.
The algorithm is a gradient-based algorithm. So we are converged when the gradient is zero.
So when is the last step valid? There's a distribution over states and an outer product of feature vectors. So when is this typically valid? It's typically valid if your state space is large and your feature vector is small. That's like one case in which it's valid. Because then assuming at least that your features are non-degenerate. So you have different features for different states. Then if there's at least as many different feature vectors that you can encounter as there are numbers in your feature vector as there are like components in your feature vector then this inner product typically exists. So this is the common case you will have many more states and you will have features that do change when you go to different states and then this outer product the expectation of that will be invertible. It's a technical assumption. Otherwise you're not guaranteed to converge.

Let's consider the TD fixed point. This converges to different thing. There's a different outer product. Instead of being the outer product of the feature itself, it's the other product of the feature with itself minus the next feature. That matrix is inverted if it exists under similar assumptions. And then times the reward times your feature vector. Not the return but the reward.
So this is a different fixed point. It's actually different from the Monte Carlo fixed point.
Typically the Monte Carlo solution is the one that you want. Because the Monte Carlo solution is defined as minimizing that thing we want. This is minimizing the difference between the return and the value. This is called the "value error" or the "return error". And this is an unbiased with respect to the using the true value instead of the return as well.
In general it's quite true that Monte Carlo typically converges to a better value than Temporal Difference learning does when you start using function approximation. However, Temporal Difference learning often converges fater.
And we can trade-off. We can pick an intermediate lambda or an intermediate n and get the best of both worlds.

The true TD error is bounded in the following way.

Temporal Difference learning update is not a true gradient update.

Temporal Difference learning does not always converge. And now I'm going to show you an example in which it doesn't. So this is an example of divergence of temporal difference learning where we have two states and our feature vector has exactly one element. And this feature vector has an element equal to 1 in the first state and the same element is equal to two in the second state. What this means is, it is depicted above the states is our value estimate in the first state is just w because it's just this number w which is also single number because our feature vectors also only has one element and we're doing linear function approximation. So our value in the first state is w and the value in the second state is 2w. Because it's just the same number w times your feature which is two. The reward along the way is 0. It's simple problem.
But now we're going to consider it's a partial problem. I didn't say what happends after you reach states where the feature vector is 2. I'm just going to consider this one transition and then, let's see what happends if we apply TD.

So let's step through that. Let's first write down the TD equation. This is Temporal difference update for parameters of the value function.
Let's consider that your weight is positive. Let's say you initialize it at 1 and let's consider a discount factor which is larger that half. This whole term here on the right will be added to the previous weight which means our new weight will be larger than the previous weight. But the weight was already positive, so we're moving away from zero. Note the true value function here would be zero.
You can expand this example to actually have a fixed point of zero, but in this case, it will continue to grow and your weight in the limit will reach infinity.
What's even worse, it tends to grow faster and faster because your weight keeps going up and this term multiplies with your weight. So this is an example of a problematic behavior of temporal difference learning.
And now we can dig into why this has happened, when this has happened, how can we characterize this and how can we avoid this.
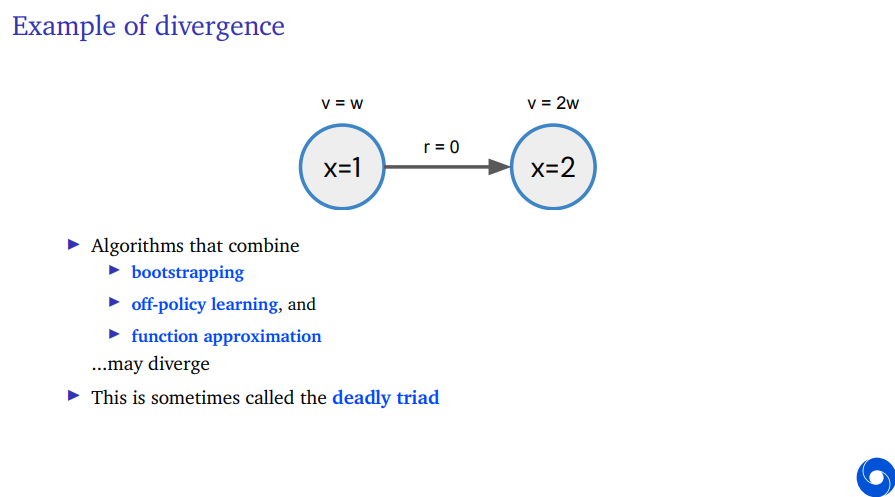
What's happening here is that, we're combining multiple different things at the same time. We're combining bootstrapping, we're bootstrapping on that state value on the right, we're combining Off-policy learning, we're combining function approximation and when you combine these three things together, you can get these divergent dynamics. This is sometimes called the deadly triad, because you need all three for this to matter for this to become a problem.
The Off-policy learning, why did I say this is Off-policy? There's no policies here, there's no actions here, so what's happening here, there's a certain dynamics and your dynamics would give you get you from this one state to the other state, but then what we're doing is, we're going to resample that transition over and over and we're never going to sample any transitions that come from the states that we've enterd just now.
And that is Off-policy in the sense that they're actually in this case. There are no policies that would sample the states over and over again specifically that way so what we're doing instead, we have an Off-policy distribution of our updates. This can emerge.
Why this is called Off-policy is, this can emerge if you're tying to predict the value of a certain policy while following a different policy, for instance in could be that the value from this state (x=2) that there are actions but we're just not interested in their values, and hence they get zeroed out in your update in some sense.

Now we could also consider On-policy updating by extending the example to be a full example and now we consider this second transition as well. Let's assume that this transition terminates with a reward of 0 and then maybe you get transitioned back to this first stage. So you see this episode over and over again but now we sample on policy which means, we sample the transition going from the second state as often as we sample the transition going to that state. If that is the case, turns out the learning dynamics, in general, are convergent. TD learning will converge also with linear function approximation if you're updating On-policy.
And indeed, it has been proven, in general, that On-policy Temporal Difference learning with linear function approximation will converge to the optimal policy that's already the optimal values in terms of its fixed point. So the fixed point of TD is still different from Monte Carlo, but if we consider that fixed point to be the goal, it will find that fixed point in the On-policy case.
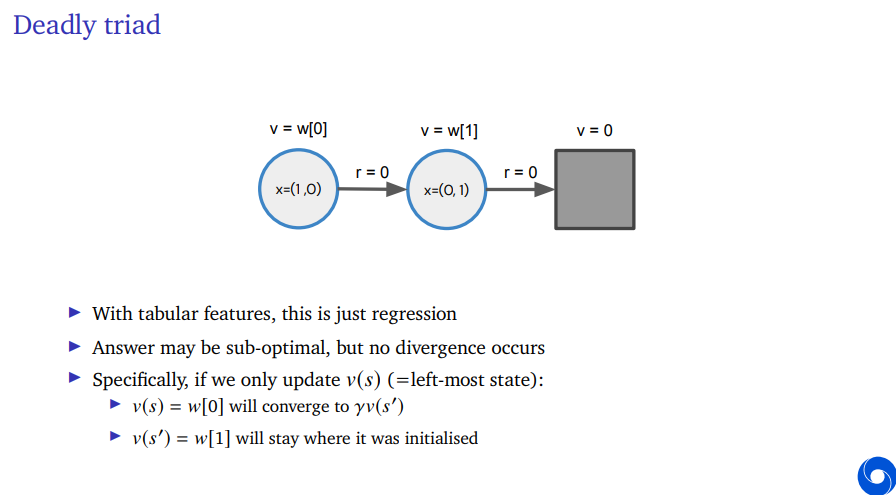
So Off-policy is a problem, On-policy fixes it. Let's dig into one of the other aspects. Function approximation as one aspect of this. So let's see what happens if we don't function approximation.



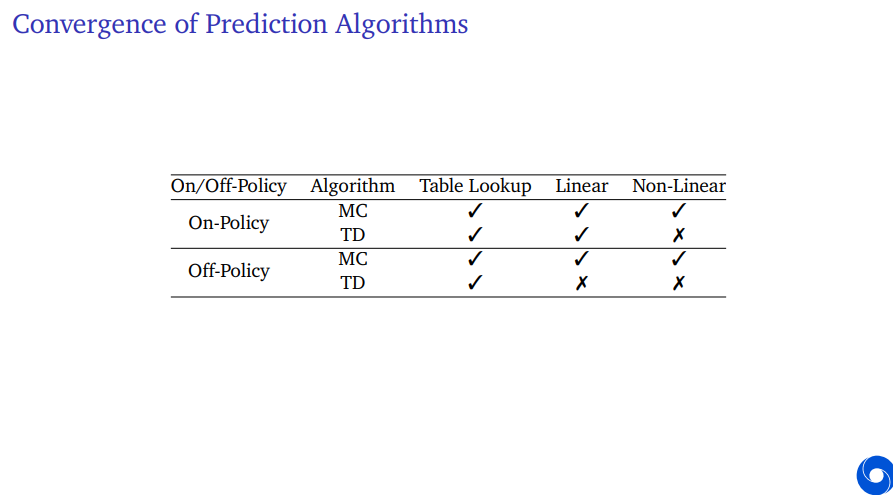
There's a couple of different categories. So you have your algorithm which could be Monte Carlo or it could be TD, it could be On-policy or it could be Off-policy. And you could pick a certain function class.
Now in terms of summarizing the convergence properties of these algorithms, if you're On-policy, you're mostly good to go. The only thing that's not 100 guaranteed is, non-linear convergence, but even for that one, we can say some cases you can guarantee that TD converges for the non-linear case. But it requires more assumptions. So we can't say in general it always converges.
If we go Off-policy, we see that linear function approximation also becomes problematic for TD. Although this doesn't mean it's always a problem. It means there are cases in which we can't guarantee convergence. It doesn't mean the algorithm doesn't work in general.



Now we're going to consider updating these functions in batch settings.





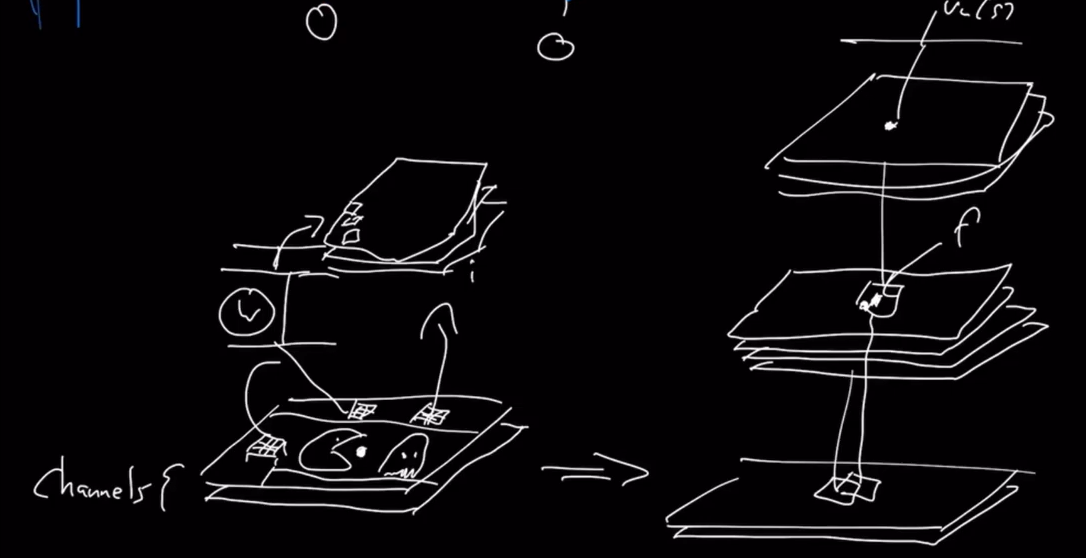


An Online neural Q-learning agent include a neural network which takes your observations and outputs an action-out Q value. So the idea is that, this is a non-linear function that looks at the pixels of the screen, let's say of pac-man, and then has some Conv layers to first do the spatial reasoning then merges that into a vector. That maybe has a couple of other layers. And then at the end, it outputs the same number of elements as you have actions. And then we index that with the action that we're interested in, if we want a specific action value.
Note that I have ignored agent state here, so the agent state is just your observation in this case. So this one wouldn't have memory and maybe that's okay for some games like pac-man.
Then we need an exploratory policies for instance. We just do epsilon greedy on top of this weight vector that we have. So that our action that we select will be greedy with respect to these action values with probability one minus epsilon, and fully random with probability epsilon.
And then we have a weight updates to the parameters of this network where we use in this case, gradient Q-learning.
Gradient Q-learning which is the Q-learning update, it's going to be your immediate reward plus the discounted value of the maximum value action in the next state minus our current estimate times the gradient of that current estimate. That would be a gradient extension of Q-learning.
Then we could use an optimizer. So typically what people do is, they take this update according to SGD, this gradient, and then they transform it for instance applying momentum. Or using more fancy optimizers like RMSProp and the Adam optimizer.

There's a neural network and the observation here is a little bit special. So the observation in DQN is not just the pixels on the screen. It's actually taking a couple of frames. A couple of steps into the past and also doing some operations on that. So the original DQN algorithm would down scale the screen slightly for computational reasons. It would gray scale it instead of keeping the color information. This actually throws away a little bit of information. Some recent approaches, people sometimes don't do that anymore.
And in addition to that, it would stack a couple of frames. So it has some slight history and there are two reasons for that. One is for instance, in a game like pong, where you're hitting a ball from one pedal to the other, it was thought that maybe this is important to be able to capture the direction of the ball. Because if you just know where the ball is, then you don't necessarily know whether it's going left or right.
There's a different reason as well, which is that India's Atari games, the screen would sometimes flicker. So certain enemies might sometimes be there on one frame but they wouldn't be there on the next frame. So therefore that was important to consider a couple of frames rather than just one frame. Otherwise a network doesn't have any memory.
'Research > RL_DeepMind' 카테고리의 다른 글
[Lecture 8] (2/2) Planning and Models (0) 2024.08.04 [Lecture 8] (1/2) Planning and Models (0) 2024.08.03 [Lecture 7] (1/2) Function Approximation (0) 2024.08.03 [Lecture 6] (2/2) Model-Free Control (0) 2024.08.02 [Lecture 6] (1/2) Model-Free Control (0) 2024.07.31