High-Resolution Image Synthesis with Latent Diffusion Models

https://arxiv.org/pdf/2112.10752

---

Abstract

By decomposing the image formation process into a sequential application of denoising autoencoders, diffusion models (DMs) achieve state-of-the-art synthesis results on image data and beyond. Additionally, their formulation allows for a guiding mechanism to control the image generation process without retraining. However, since these models typically operate directly in pixel space, optimization of powerful DMs often consumes hundreds of GPU days and inference is expensive due to sequential evaluations. To enable DM training on limited computational resources while retaining their quality and flexibility, we apply them in the latent space of powerful pretrained autoencoders. In contrast to previous work, training diffusion models on such a representation allows for the first time to reach a near-optimal point between complexity reduction and detail preservation, greatly boosting visual fidelity. By introducing cross-attention layers into the model architecture, we turn diffusion models into powerful and flexible generators for general conditioning inputs such as text or bounding boxes and high-resolution synthesis becomes possible in a convolutional manner. Our latent diffusion models (LDMs) achieve new state-of-the-art scores for image inpainting and class-conditional image synthesis and highly competitive performance on various tasks, including text-to-image synthesis, unconditional image generation and super-resolution, while significantly reducing computational requirements compared to pixel-based DMs.

---

1. Introduction

Image synthesis is one of the computer vision fields with the most spectacular recent development, but also among those with the greatest computational demands. Especially high-resolution synthesis of complex, natural scenes is presently dominated by scaling up likelihood-based models, potentially containing billions of parameters in autoregressive (AR) transformers [66,67]. In contrast, the promising results of GANs [3, 27, 40] have been revealed to be mostly confined to data with comparably limited variability as their adversarial learning procedure does not easily scale to modeling complex, multi-modal distributions. Recently, diffusion models [82], which are built from a hierarchy of denoising autoencoders, have shown to achieve impressive results in image synthesis [30,85] and beyond [7,45,48,57], and define the state-of-the-art in class-conditional image synthesis [15,31] and super-resolution [72]. Moreover, even unconditional DMs can readily be applied to tasks such as inpainting and colorization [85] or stroke-based synthesis [53], in contrast to other types of generative models [19,46,69]. Being likelihood-based models, they do not exhibit mode-collapse and training instabilities as GANs and, by heavily exploiting parameter sharing, they can model highly complex distributions of natural images without involving billions of parameters as in AR models [67].

Democratizing High-Resolution Image Synthesis

DMs belong to the class of likelihood-based models, whose mode-covering behavior makes them prone to spend excessive amounts of capacity (and thus compute resources) on modeling imperceptible details of the data [16, 73]. Although the reweighted variational objective [30] aims to address this by undersampling the initial denoising steps, DMs are still computationally demanding, since training and evaluating such a model requires repeated function evaluations (and gradient computations) in the high-dimensional space of RGB images. As an example, training the most powerful DMs often takes hundreds of GPU days (e.g. 150 - 1000 V100 days in [15]) and repeated evaluations on a noisy version of the input space render also inference expensive, so that producing 50k samples takes approximately 5 days [15] on a single A100 GPU. This has two consequences for the research community and users in general: Firstly, training such a model requires massive computational resources only available to a small fraction of the field, and leaves a huge carbon footprint [65, 86]. Secondly, evaluating an already trained model is also expensive in time and memory, since the same model architecture must run sequentially for a large number of steps (e.g. 25 - 1000 steps in [15]).

 

To increase the accessibility of this powerful model class and at the same time reduce its significant resource consumption, a method is needed that reduces the computational complexity for both training and sampling. Reducing the computational demands of DMs without impairing their performance is, therefore, key to enhance their accessibility.

Departure to Latent Space

 

Our approach starts with the analysis of already trained diffusion models in pixel space: Fig. 2 shows the rate-distortion trade-off of a trained model. As with any likelihood-based model, learning can be roughly divided into two stages: First is a perceptual compression stage which removes high-frequency details but still learns little semantic variation. In the second stage, the actual generative model learns the semantic and conceptual composition of the data (semantic compression). We thus aim to first find a perceptually equivalent, but computationally more suitable space, in which we will train diffusion models for high-resolution image synthesis.

 

Following common practice [11, 23, 66, 67, 96], we separate training into two distinct phases: First, we train an autoencoder which provides a lower-dimensional (and thereby efficient) representational space which is perceptually equivalent to the data space. Importantly, and in contrast to previous work [23,66], we do not need to rely on excessive spatial compression, as we train DMs in the learned latent space, which exhibits better scaling properties with respect to the spatial dimensionality. The reduced complexity also provides efficient image generation from the latent space with a single network pass. We dub the resulting model class Latent Diffusion Models (LDMs).

 

A notable advantage of this approach is that we need to train the universal autoencoding stage only once and can therefore reuse it for multiple DM trainings or to explore possibly completely different tasks [81]. This enables efficient exploration of a large number of diffusion models for various image-to-image and text-to-image tasks. For the latter, we design an architecture that connects transformers to the DM’s UNet backbone [71] and enables arbitrary types of token-based conditioning mechanisms, see Sec. 3.3.

In sum, our work makes the following contributions:

 

(i) In contrast to purely transformer-based approaches [23, 66], our method scales more graceful to higher dimensional data and can thus (a) work on a compression level which provides more faithful and detailed reconstructions than previous work (see Fig. 1) and (b) can be efficiently applied to high-resolution synthesis of megapixel images.

 

(ii) We achieve competitive performance on multiple tasks (unconditional image synthesis, inpainting, stochastic super-resolution) and datasets while significantly lowering computational costs. Compared to pixel-based diffusion approaches, we also significantly decrease inference costs.

 

(iii) We show that, in contrast to previous work [93] which learns both an encoder/decoder architecture and a score-based prior simultaneously, our approach does not require a delicate weighting of reconstruction and generative abilities. This ensures extremely faithful reconstructions and requires very little regularization of the latent space.

 

(iv) We find that for densely conditioned tasks such as super-resolution, inpainting and semantic synthesis, our model can be applied in a convolutional fashion and render large, consistent images of ∼ 1024^2 px.

 

(v) Moreover, we design a general-purpose conditioning mechanism based on cross-attention, enabling multi-modal training. We use it to train class-conditional, text-to-image and layout-to-image models.

 

(vi) Finally, we release pretrained latent diffusion and autoencoding models at https://github.com/CompVis/latent-diffusion  which might be reusable for a various tasks besides training of DMs [81].

---

2. Related Work

Generative Models for Image Synthesis

The high dimensional nature of images presents distinct challenges to generative modeling. Generative Adversarial Networks (GAN) [27] allow for efficient sampling of high resolution images with good perceptual quality [3, 42], but are difficult to optimize [2, 28, 54] and struggle to capture the full data distribution [55]. In contrast, likelihood-based methods emphasize good density estimation which renders optimization more well-behaved. Variational autoencoders (VAE) [46] and flow-based models [18, 19] enable efficient synthesis of high resolution images [9, 44, 92], but sample quality is not on par with GANs. While autoregressive models (ARM) [6, 10, 94, 95] achieve strong performance in density estimation, computationally demanding architectures [97] and a sequential sampling process limit them to low resolution images. Because pixel based representations of images contain barely perceptible, high-frequency details [16,73], maximum-likelihood training spends a disproportionate amount of capacity on modeling them, resulting in long training times. To scale to higher resolutions, several two-stage approaches [23,67,101,103] use ARMs to model a compressed latent image space instead of raw pixels.

Recently, Diffusion Probabilistic Models (DM)

[82], have achieved state-of-the-art results in density estimation [45] as well as in sample quality [15]. The generative power of these models stems from a natural fit to the inductive biases of image-like data when their underlying neural backbone is implemented as a UNet [15, 30, 71, 85]. The best synthesis quality is usually achieved when a reweighted objective [30] is used for training. In this case, the DM corresponds to a lossy compressor and allow to trade image quality for compression capabilities. Evaluating and optimizing these models in pixel space, however, has the downside of low inference speed and very high training costs. While the former can be partially adressed by advanced sampling strategies [47, 75, 84] and hierarchical approaches [31, 93], training on high-resolution image data always requires to calculate expensive gradients. We adress both drawbacks with our proposed LDMs, which work on a compressed latent space of lower dimensionality. This renders training computationally cheaper and speeds up inference with almost no reduction in synthesis quality (see Fig. 1).

Two-Stage Image Synthesis

To mitigate the shortcomings of individual generative approaches, a lot of research [11, 23, 67, 70, 101, 103] has gone into combining the strengths of different methods into more efficient and performant models via a two stage approach. VQ-VAEs [67, 101] use autoregressive models to learn an expressive prior over a discretized latent space. [66] extend this approach to text-to-image generation by learning a joint distributation over discretized image and text representations. More generally, [70] uses conditionally invertible networks to provide a generic transfer between latent spaces of diverse domains. Different from VQ-VAEs, VQGANs [23, 103] employ a first stage with an adversarial and perceptual objective to scale autoregressive transformers to larger images. However, the high compression rates required for feasible ARM training, which introduces billions of trainable parameters [23, 66], limit the overall performance of such approaches and less compression comes at the price of high computational cost [23, 66]. Our work prevents such tradeoffs, as our proposed LDMs scale more gently to higher dimensional latent spaces due to their convolutional backbone. Thus, we are free to choose the level of compression which optimally mediates between learning a powerful first stage, without leaving too much perceptual compression up to the generative diffusion model while guaranteeing highfidelity reconstructions (see Fig. 1).

 

While approaches to jointly [93] or separately [80] learn an encoding/decoding model together with a score-based prior exist, the former still require a difficult weighting between reconstruction and generative capabilities [11] and are outperformed by our approach (Sec. 4), and the latter focus on highly structured images such as human faces.

---

3. Method

To lower the computational demands of training diffusion models towards high-resolution image synthesis, we observe that although diffusion models allow to ignore perceptually irrelevant details by undersampling the corresponding loss terms [30], they still require costly function evaluations in pixel space, which causes huge demands in computation time and energy resources.

 

We propose to circumvent this drawback by introducing an explicit separation of the compressive from the generative learning phase (see Fig. 2). To achieve this, we utilize an autoencoding model which learns a space that is perceptually equivalent to the image space, but offers significantly reduced computational complexity.

 

Such an approach offers several advantages: (i) By leaving the high-dimensional image space, we obtain DMs which are computationally much more efficient because sampling is performed on a low-dimensional space. (ii) We exploit the inductive bias of DMs inherited from their UNet architecture [71], which makes them particularly effective for data with spatial structure and therefore alleviates the need for aggressive, quality-reducing compression levels as required by previous approaches [23, 66]. (iii) Finally, we obtain general-purpose compression models whose latent space can be used to train multiple generative models and which can also be utilized for other downstream applications such as single-image CLIP-guided synthesis [25].

---

3.1. Perceptual Image Compression

Our perceptual compression model is based on previous work [23] and consists of an autoencoder trained by combination of a perceptual loss [106] and a patch-based [33] adversarial objective [20, 23, 103]. This ensures that the reconstructions are confined to the image manifold by enforcing local realism and avoids bluriness introduced by relying solely on pixel-space losses such as L_2 or L_1 objectives.

 

More precisely, given an image x ∈ R^H×W×3 in RGB space, the encoder E encodes x into a latent representation z = E(x), and the decoder D reconstructs the image from the latent, giving x˜ = D(z) = D(E(x)), where z ∈ R^h×w×c . Importantly, the encoder downsamples the image by a factor f = H/h = W/w, and we investigate different downsampling factors f = 2^m, with m ∈ N.

 

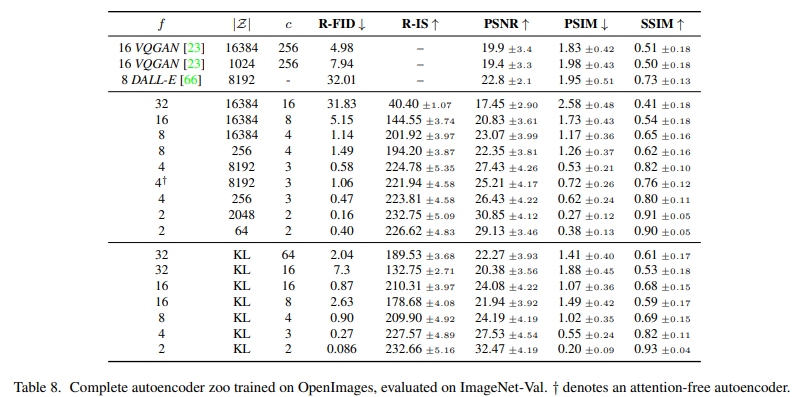
In order to avoid arbitrarily high-variance latent spaces, we experiment with two different kinds of regularizations. The first variant, KL-reg., imposes a slight KL-penalty towards a standard normal on the learned latent, similar to a VAE [46, 69], whereas VQ-reg. uses a vector quantization layer [96] within the decoder. This model can be interpreted as a VQGAN [23] but with the quantization layer absorbed by the decoder. Because our subsequent DM is designed to work with the two-dimensional structure of our learned latent space z = E(x), we can use relatively mild compression rates and achieve very good reconstructions. This is in contrast to previous works [23, 66], which relied on an arbitrary 1D ordering of the learned space z to model its distribution autoregressively and thereby ignored much of the inherent structure of z. Hence, our compression model preserves details of x better (see Tab. 8). The full objective and training details can be found in the supplement.

---

3.2. Latent Diffusion Models

Diffusion Models

[82] are probabilistic models designed to learn a data distribution p(x) by gradually denoising a normally distributed variable, which corresponds to learning the reverse process of a fixed Markov Chain of length T. For image synthesis, the most successful models [15,30,72] rely on a reweighted variant of the variational lower bound on p(x), which mirrors denoising score-matching [85]. These models can be interpreted as an equally weighted sequence of denoising autoencoders εθ(xt, t); t = 1 . . . T, which are trained to predict a denoised variant of their input xt, where xt is a noisy version of the input x. The corresponding objective can be simplified to (Sec. B)

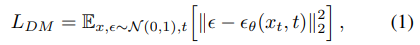
with t uniformly sampled from {1, . . . , T}.

Generative Modeling of Latent Representations

With our trained perceptual compression models consisting of E and D, we now have access to an efficient, low-dimensional latent space in which high-frequency, imperceptible details are abstracted away. Compared to the high-dimensional pixel space, this space is more suitable for likelihood-based generative models, as they can now (i) focus on the important, semantic bits of the data and (ii) train in a lower dimensional, computationally much more efficient space.

 

Unlike previous work that relied on autoregressive, attention-based transformer models in a highly compressed, discrete latent space [23,66,103], we can take advantage of image-specific inductive biases that our model offers. This includes the ability to build the underlying UNet primarily from 2D convolutional layers, and further focusing the objective on the perceptually most relevant bits using the reweighted bound, which now reads

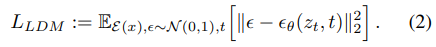
The neural backbone εθ(◦, t) of our model is realized as a time-conditional UNet [71]. Since the forward process is fixed, z_t can be efficiently obtained from E during training, and samples from p(z) can be decoded to image space with a single pass through D.

---

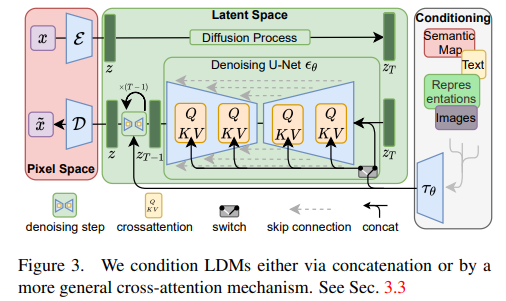
3.3. Conditioning Mechanisms

Similar to other types of generative models [56, 83], diffusion models are in principle capable of modeling conditional distributions of the form p(z|y). This can be implemented with a conditional denoising autoencoder εθ(zt, t, y) and paves the way to controlling the synthesis process through inputs y such as text [68], semantic maps [33, 61] or other image-to-image translation tasks [34].

 

In the context of image synthesis, however, combining the generative power of DMs with other types of conditionings beyond class-labels [15] or blurred variants of the input image [72] is so far an under-explored area of research.

 

We turn DMs into more flexible conditional image generators by augmenting their underlying UNet backbone with the cross-attention mechanism [97], which is effective for learning attention-based models of various input modalities [35,36]. To pre-process y from various modalities (such as language prompts) we introduce a domain specific encoder τ_θ that projects y to an intermediate representation τ_θ(y) ∈ R^M×d_τ , which is then mapped to the intermediate layers of the UNet via a cross-attention layer implementing

 

where both τθ and εθ are jointly optimized via Eq. 3. This conditioning mechanism is flexible as τθ can be parameterized with domain-specific experts, e.g. (unmasked) transformers [97] when y are text prompts (see Sec. 4.3.1)

---

4. Experiments

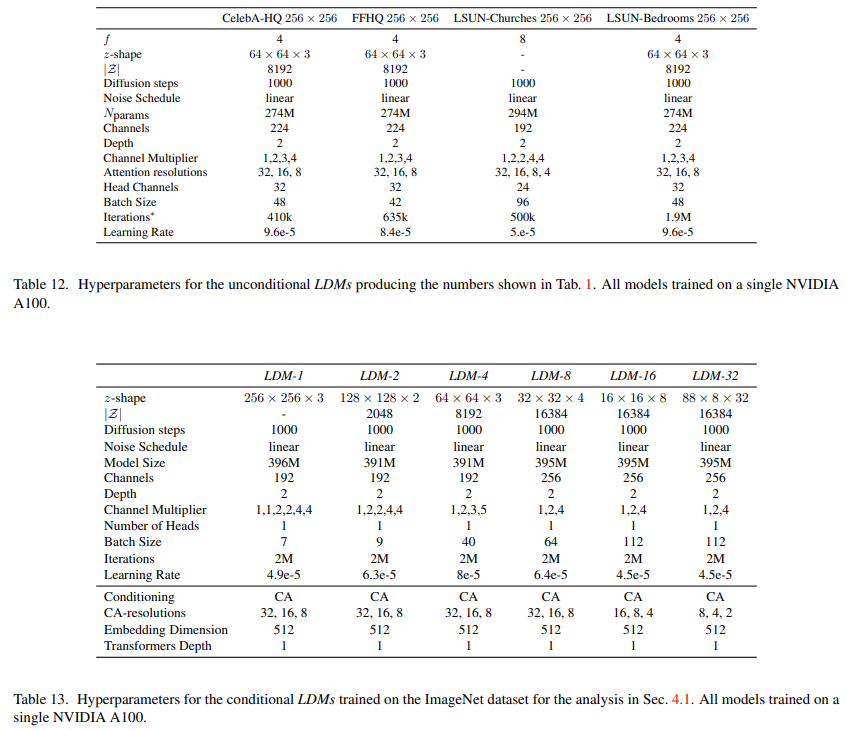
LDMs provide means to flexible and computationally tractable diffusion based image synthesis of various image modalities, which we empirically show in the following. Firstly, however, we analyze the gains of our models compared to pixel-based diffusion models in both training and inference. Interestingly, we find that LDMs trained in VQ-regularized latent spaces sometimes achieve better sample quality, even though the reconstruction capabilities of VQ-regularized first stage models slightly fall behind those of their continuous counterparts, cf. Tab. 8. A visual comparison between the effects of first stage regularization schemes on LDM training and their generalization abilities to resolutions > 256^2 can be found in Appendix D.1. In E.2 we list details on architecture, implementation, training and evaluation for all results presented in this section.

---

4.1. On Perceptual Compression Tradeoffs

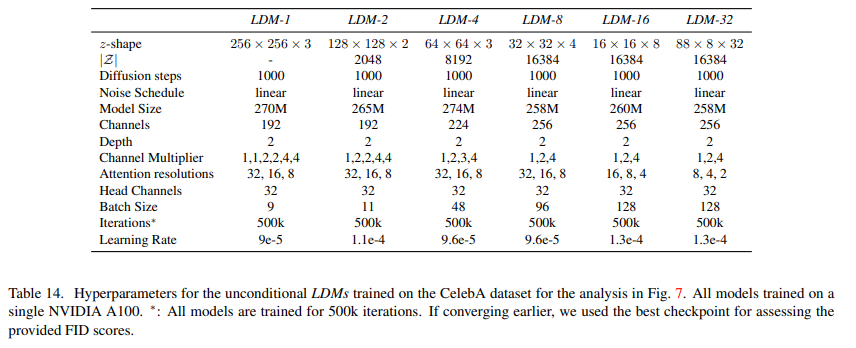
This section analyzes the behavior of our LDMs with different downsampling factors f ∈ {1, 2, 4, 8, 16, 32} (abbreviated as LDM-f, where LDM-1 corresponds to pixel-based DMs). To obtain a comparable test-field, we fix the computational resources to a single NVIDIA A100 for all experiments in this section and train all models for the same number of steps and with the same number of parameters.

 

Tab. 8 shows hyperparameters and reconstruction performance of the first stage models used for the LDMs compared in this section. Fig. 6 shows sample quality as a function of training progress for 2M steps of class-conditional models on the ImageNet [12] dataset. We see that, i) small downsampling factors for LDM-{1,2} result in slow training progress, whereas ii) overly large values of f cause stagnating fidelity after comparably few training steps. Revisiting the analysis above (Fig. 1 and 2) we attribute this to i) leaving most of perceptual compression to the diffusion model and ii) too strong first stage compression resulting in information loss and thus limiting the achievable quality. LDM-{4-16} strike a good balance between efficiency and perceptually faithful results, which manifests in a significant FID [29] gap of 38 between pixel-based diffusion (LDM-1) and LDM-8 after 2M training steps.

 

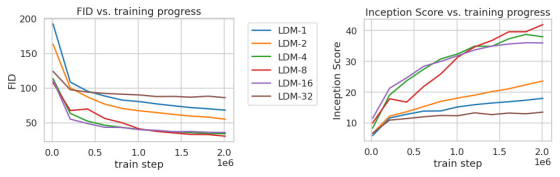
In Fig. 7, we compare models trained on CelebAHQ [39] and ImageNet in terms sampling speed for different numbers of denoising steps with the DDIM sampler [84] and plot it against FID-scores [29]. LDM-{4-8} outperform models with unsuitable ratios of perceptual and conceptual compression. Especially compared to pixel-based LDM-1, they achieve much lower FID scores while simultaneously significantly increasing sample throughput. Complex datasets such as ImageNet require reduced compression rates to avoid reducing quality. In summary, LDM-4 and -8 offer the best conditions for achieving high-quality synthesis results.

---

4.2. Image Generation with Latent Diffusion

 

We train unconditional models of 256^2 images on CelebA-HQ [39], FFHQ [41], LSUN-Churches and -Bedrooms [102] and evaluate the i) sample quality and ii) their coverage of the data manifold using ii) FID [29] and ii) Precision-and-Recall [50]. Tab. 1 summarizes our results. On CelebA-HQ, we report a new state-of-the-art FID of 5.11, outperforming previous likelihood-based models as well as GANs. We also outperform LSGM [93] where a latent diffusion model is trained jointly together with the first stage. In contrast, we train diffusion models in a fixed space and avoid the difficulty of weighing reconstruction quality against learning the prior over the latent space, see Fig. 1-2.

 

We outperform prior diffusion based approaches on all but the LSUN-Bedrooms dataset, where our score is close to ADM [15], despite utilizing half its parameters and requiring 4-times less train resources (see Appendix E.3.5). Moreover, LDMs consistently improve upon GAN-based methods in Precision and Recall, thus confirming the advantages of their mode-covering likelihood-based training objective over adversarial approaches. In Fig. 4 we also show qualitative results on each dataset.

---

4.3. Conditional Latent Diffusion

4.3.1. Transformer Encoders for LDMs

 

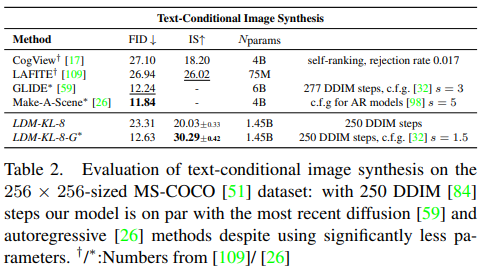
By introducing cross-attention based conditioning into LDMs we open them up for various conditioning modalities previously unexplored for diffusion models. For text-to-image image modeling, we train a 1.45B parameter KL-regularized LDM conditioned on language prompts on LAION-400M [78]. We employ the BERT-tokenizer [14] and implement τθ as a transformer [97] to infer a latent code which is mapped into the UNet via (multi-head) crossattention (Sec. 3.3). This combination of domain specific experts for learning a language representation and visual synthesis results in a powerful model, which generalizes well to complex, user-defined text prompts, cf . Fig. 8 and 5. For quantitative analysis, we follow prior work and evaluate text-to-image generation on the MS-COCO [51] validation set, where our model improves upon powerful AR [17, 66] and GAN-based [109] methods, cf . Tab. 2. We note that applying classifier-free diffusion guidance [32] greatly boosts sample quality, such that the guided LDM-KL-8-G is on par with the recent state-of-the-art AR [26] and diffusion models [59] for text-to-image synthesis, while substantially reducing parameter count. To further analyze the flexibility of the cross-attention based conditioning mechanism we also train models to synthesize images based on semantic layouts on OpenImages [49], and finetune on COCO [4], see Fig. 8. See Sec. D.3 for the quantitative evaluation and implementation details.

 

Lastly, following prior work [3, 15, 21, 23], we evaluate our best-performing class-conditional ImageNet models with f ∈ {4, 8} from Sec. 4.1 in Tab. 3, Fig. 4 and Sec. D.4. Here we outperform the state of the art diffusion model ADM [15] while significantly reducing computational requirements and parameter count, cf . Tab 18.

---

4.3.2. Convolutional Sampling Beyond 256^2

By concatenating spatially aligned conditioning information to the input of εθ, LDMs can serve as efficient general purpose image-to-image translation models. We use this to train models for semantic synthesis, super-resolution (Sec. 4.4) and inpainting (Sec. 4.5). For semantic synthesis, we use images of landscapes paired with semantic maps [23, 61] and concatenate downsampled versions of the semantic maps with the latent image representation of a f = 4 model (VQ-reg., see Tab. 8). We train on an input resolution of 256^2 (crops from 384^2 ) but find that our model generalizes to larger resolutions and can generate images up to the megapixel regime when evaluated in a convolutional manner (see Fig. 9). We exploit this behavior to also apply the super-resolution models in Sec. 4.4 and the inpainting models in Sec. 4.5 to generate large images between 512^2 and 1024^2 . For this application, the signal-to-noise ratio (induced by the scale of the latent space) significantly affects the results. In Sec. D.1 we illustrate this when learning an LDM on (i) the latent space as provided by a f = 4 model (KL-reg., see Tab. 8), and (ii) a rescaled version, scaled by the component-wise standard deviation.

 

The latter, in combination with classifier-free guidance [32], also enables the direct synthesis of > 256^2 images for the text-conditional LDM-KL-8-G as in Fig. 13.

---

4.4. Super-Resolution with Latent Diffusion

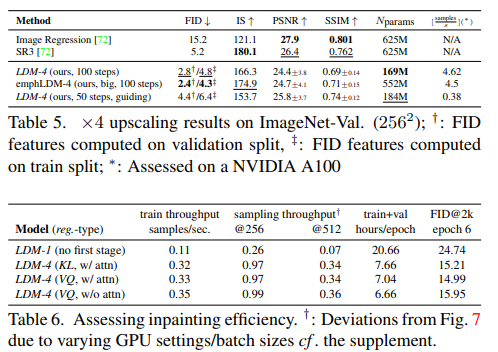
LDMs can be efficiently trained for super-resolution by diretly conditioning on low-resolution images via concatenation (cf . Sec. 3.3). In a first experiment, we follow SR3 [72] and fix the image degradation to a bicubic interpolation with 4×-downsampling and train on ImageNet following SR3’s data processing pipeline. We use the f = 4 autoencoding model pretrained on OpenImages (VQ-reg., cf . Tab. 8) and concatenate the low-resolution conditioning y and the inputs to the UNet, i.e. τθ is the identity. Our qualitative and quantitative results (see Fig. 10 and Tab. 5) show competitive performance and LDM-SR outperforms SR3 in FID while SR3 has a better IS. A simple image regression model achieves the highest PSNR and SSIM scores; however these metrics do not align well with human perception [106] and favor blurriness over imperfectly aligned high frequency details [72]. Further, we conduct a user study comparing the pixel-baseline with LDM-SR. We follow SR3 [72] where human subjects were shown a low-res image in between two high-res images and asked for preference. The results in Tab. 4 affirm the good performance of LDM-SR. PSNR and SSIM can be pushed by using a post-hoc guiding mechanism [15] and we implement this image-based guider via a perceptual loss, see Sec. D.6.

 

Since the bicubic degradation process does not generalize well to images which do not follow this pre-processing, we also train a generic model, LDM-BSR, by using more diverse degradation. The results are shown in Sec. D.6.1.

---

4.5. Inpainting with Latent Diffusion

Inpainting is the task of filling masked regions of an image with new content either because parts of the image are are corrupted or to replace existing but undesired content within the image. We evaluate how our general approach for conditional image generation compares to more specialized, state-of-the-art approaches for this task. Our evaluation follows the protocol of LaMa [88], a recent inpainting model that introduces a specialized architecture relying on Fast Fourier Convolutions [8]. The exact training & evaluation protocol on Places [108] is described in Sec. E.2.2.

 

We first analyze the effect of different design choices for the first stage. In particular, we compare the inpainting efficiency of LDM-1 (i.e. a pixel-based conditional DM) with LDM-4, for both KL and VQ regularizations, as well as VQ-LDM-4 without any attention in the first stage (see Tab. 8), where the latter reduces GPU memory for decoding at high resolutions. For comparability, we fix the number of parameters for all models. Tab. 6 reports the training and sampling throughput at resolution 2562 and 5122 , the total training time in hours per epoch and the FID score on the validation split after six epochs. Overall, we observe a speed-up of at least 2.7× between pixel- and latent-based diffusion models while improving FID scores by a factor of at least 1.6×.

 

The comparison with other inpainting approaches in Tab. 7 shows that our model with attention improves the overall image quality as measured by FID over that of [88]. LPIPS between the unmasked images and our samples is slightly higher than that of [88]. We attribute this to [88] only producing a single result which tends to recover more of an average image compared to the diverse results produced by our LDM cf . Fig. 21. Additionally in a user study (Tab. 4) human subjects favor our results over those of [88].

 

Based on these initial results, we also trained a larger diffusion model (big in Tab. 7) in the latent space of the VQregularized first stage without attention. Following [15], the UNet of this diffusion model uses attention layers on three levels of its feature hierarchy, the BigGAN [3] residual block for up- and downsampling and has 387M parameters instead of 215M. After training, we noticed a discrepancy in the quality of samples produced at resolutions 256^2 and 512^2 , which we hypothesize to be caused by the additional attention modules. However, fine-tuning the model for half an epoch at resolution 512^2 allows the model to adjust to the new feature statistics and sets a new state of the art FID on image inpainting (big, w/o attn, w/ ft in Tab. 7, Fig. 11.).

---

5. Limitations & Societal Impact

Limitations

While LDMs significantly reduce computational requirements compared to pixel-based approaches, their sequential sampling process is still slower than that of GANs. Moreover, the use of LDMs can be questionable when high precision is required: although the loss of image quality is very small in our f = 4 autoencoding models (see Fig. 1), their reconstruction capability can become a bottleneck for tasks that require fine-grained accuracy in pixel space. We assume that our superresolution models (Sec. 4.4) are already somewhat limited in this respect.

Societal Impact

Generative models for media like imagery are a double-edged sword: On the one hand, they enable various creative applications, and in particular approaches like ours that reduce the cost of training and inference have the potential to facilitate access to this technology and democratize its exploration. On the other hand, it also means that it becomes easier to create and disseminate manipulated data or spread misinformation and spam. In particular, the deliberate manipulation of images (“deep fakes”) is a common problem in this context, and women in particular are disproportionately affected by it [13, 24].

 

Generative models can also reveal their training data [5, 90], which is of great concern when the data contain sensitive or personal information and were collected without explicit consent. However, the extent to which this also applies to DMs of images is not yet fully understood.

 

Finally, deep learning modules tend to reproduce or exacerbate biases that are already present in the data [22, 38, 91]. While diffusion models achieve better coverage of the data distribution than e.g. GAN-based approaches, the extent to which our two-stage approach that combines adversarial training and a likelihood-based objective misrepresents the data remains an important research question.

 

For a more general, detailed discussion of the ethical considerations of deep generative models, see e.g. [13].

---

6. Conclusion

We have presented latent diffusion models, a simple and efficient way to significantly improve both the training and sampling efficiency of denoising diffusion models without degrading their quality. Based on this and our cross-attention conditioning mechanism, our experiments could demonstrate favorable results compared to state-of-the-art methods across a wide range of conditional image synthesis tasks without task-specific architectures.

---

Appendix

---

B. Detailed Information on Denoising Diffusion Models

---

C. Image Guiding Mechanisms

 

An intriguing feature of diffusion models is that unconditional models can be conditioned at test-time [15, 82, 85]. In particular, [15] presented an algorithm to guide both unconditional and conditional models trained on the ImageNet dataset with a classifier log pΦ(y|xt), trained on each xt of the diffusion process. We directly build on this formulation and introduce post-hoc image-guiding:

 

For an epsilon-parameterized model with fixed variance, the guiding algorithm as introduced in [15] reads:

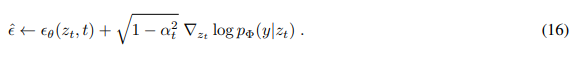
This can be interpreted as an update correcting the “score”  εθ with a conditional distribution log pΦ(y|zt).

 

So far, this scenario has only been applied to single-class classification models. We re-interpret the guiding distribution pΦ(y|T(D(z0(zt)))) as a general purpose image-to-image translation task given a target image y, where T can be any differentiable transformation adopted to the image-to-image translation task at hand, such as the identity, a downsampling operation or similar.

 

As an example, we can assume a Gaussian guider with fixed variance σ^2 = 1, such that

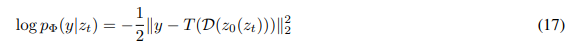
becomes a L2 regression objective.

 

Fig. 14 demonstrates how this formulation can serve as an upsampling mechanism of an unconditional model trained on 256^2 images, where unconditional samples of size 256^2 guide the convolutional synthesis of 512^2 images and T is a 2× bicubic downsampling. Following this motivation, we also experiment with a perceptual similarity guiding and replace the L2 objective with the LPIPS [106] metric, see Sec. 4.4.

---

D. Additional Results

D.1. Choosing the Signal-to-Noise Ratio for High-Resolution Synthesis

 

As discussed in Sec. 4.3.2, the signal-to-noise ratio induced by the variance of the latent space (i.e. Var(z)/σ^2_t) significantly affects the results for convolutional sampling. For example, when training a LDM directly in the latent space of a KL-regularized model (see Tab. 8), this ratio is very high, such that the model allocates a lot of semantic detail early on in the reverse denoising process. In contrast, when rescaling the latent space by the component-wise standard deviation of the latents as described in Sec. G, the SNR is descreased. We illustrate the effect on convolutional sampling for semantic image synthesis in Fig. 15. Note that the VQ-regularized space has a variance close to 1, such that it does not have to be rescaled.

---

D.2. Full List of all First Stage Models

We provide a complete list of various autoenconding models trained on the OpenImages dataset in Tab. 8.

---

D.3. Layout-to-Image Synthesis

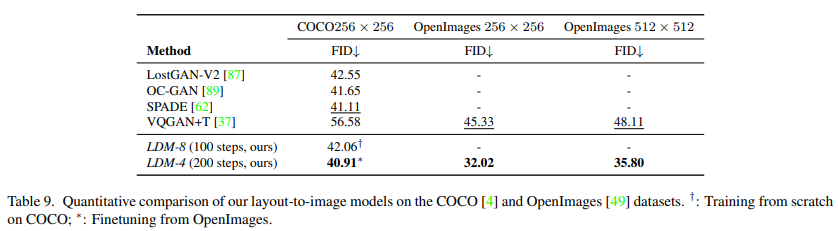
Here we provide the quantitative evaluation and additional samples for our layout-to-image models from Sec. 4.3.1. We train a model on the COCO [4] and one on the OpenImages [49] dataset, which we subsequently additionally finetune on COCO. Tab 9 shows the result. Our COCO model reaches the performance of recent state-of-the art models in layout-to-image synthesis, when following their training and evaluation protocol [89]. When finetuning from the OpenImages model, we surpass these works. Our OpenImages model surpasses the results of Jahn et al [37] by a margin of nearly 11 in terms of FID. In Fig. 16 we show additional samples of the model finetuned on COCO.

---

D.4. Class-Conditional Image Synthesis on ImageNet

 

Tab. 10 contains the results for our class-conditional LDM measured in FID and Inception score (IS). LDM-8 requires significantly fewer parameters and compute requirements (see Tab. 18) to achieve very competitive performance. Similar to previous work, we can further boost the performance by training a classifier on each noise scale and guiding with it, see Sec. C. Unlike the pixel-based methods, this classifier is trained very cheaply in latent space. For additional qualitative results, see Fig. 26 and Fig. 27.

---

D.5. Sample Quality vs. V100 Days (Continued from Sec. 4.1)

 

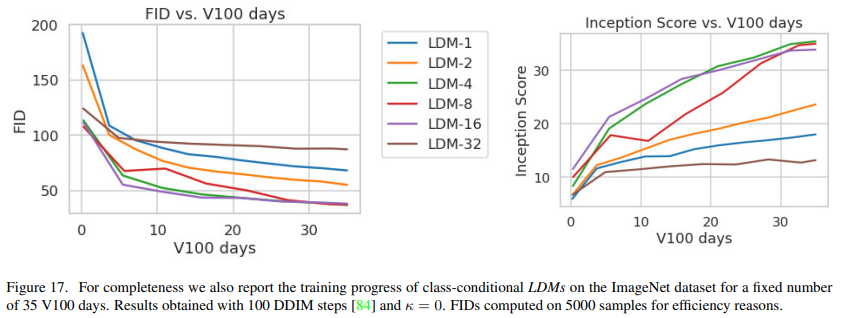
For the assessment of sample quality over the training progress in Sec. 4.1, we reported FID and IS scores as a function of train steps. Another possibility is to report these metrics over the used resources in V100 days. Such an analysis is additionally provided in Fig. 17, showing qualitatively similar results.

---

D.6. Super-Resolution

 

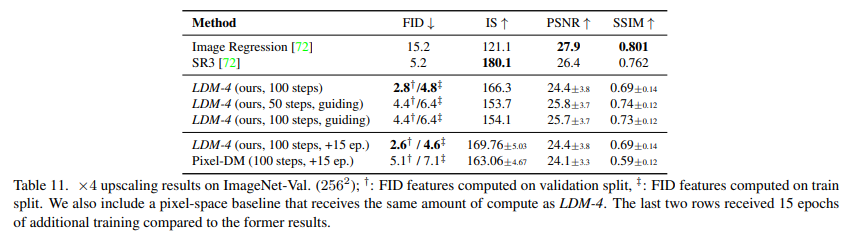
For better comparability between LDMs and diffusion models in pixel space, we extend our analysis from Tab. 5 by comparing a diffusion model trained for the same number of steps and with a comparable number 1 of parameters to our LDM. The results of this comparison are shown in the last two rows of Tab. 11 and demonstrate that LDM achieves better performance while allowing for significantly faster sampling. A qualitative comparison is given in Fig. 20 which shows random samples from both LDM and the diffusion model in pixel space.

---

E. Implementation Details and Hyperparameters

E.1. Hyperparameters

We provide an overview of the hyperparameters of all trained LDM models in Tab. 12, Tab. 13, Tab. 14 and Tab. 15.

---

E.2. Implementation Details

E.2.1. Implementations of τθ for conditional LDMs

For the experiments on text-to-image and layout-to-image (Sec. 4.3.1) synthesis, we implement the conditioner τθ as an unmasked transformer which processes a tokenized version of the input y and produces an output ζ := τθ(y), where ζ ∈ R^M×dτ . More specifically, the transformer is implemented from N transformer blocks consisting of global self-attention layers, layer-normalization and position-wise MLPs as follows 2 (adapted from https://github.com/lucidrains/x-transformers ):

With ζ available, the conditioning is mapped into the UNet via the cross-attention mechanism as depicted in Fig. 3. We modify the “ablated UNet” [15] architecture and replace the self-attention layer with a shallow (unmasked) transformer consisting of T blocks with alternating layers of (i) self-attention, (ii) a position-wise MLP and (iii) a cross-attention layer;

 

see Tab. 16. Note that without (ii) and (iii), this architecture is equivalent to the “ablated UNet”.

 

While it would be possible to increase the representational power of τθ by additionally conditioning on the time step t, we do not pursue this choice as it reduces the speed of inference. We leave a more detailed analysis of this modification to future work.

 

For the text-to-image model, we rely on a publicly available3 tokenizer [99] ( 3https://huggingface.co/transformers/model_doc/bert.html#berttokenizerfast ). The layout-to-image model discretizes the spatial locations of the bounding boxes and encodes each box as a (l, b, c)-tuple, where l denotes the (discrete) top-left and b the bottom-right position. Class information is contained in c.

 

See Tab. 17 for the hyperparameters of τθ and Tab. 13 for those of the UNet for both of the above tasks.

 

Note that the class-conditional model as described in Sec. 4.1 is also implemented via cross-attention, where τθ is a single learnable embedding layer with a dimensionality of 512, mapping classes y to ζ ∈ R 1×512 .

---

G. Details on Autoencoder Models

We train all our autoencoder models in an adversarial manner following [23], such that a patch-based discriminator Dψ is optimized to differentiate original images from reconstructions D(E(x)). To avoid arbitrarily scaled latent spaces, we regularize the latent z to be zero centered and obtain small variance by introducing an regularizing loss term L_reg. We investigate two different regularization methods: (i) a low-weighted Kullback-Leibler-term between q_E(z|x) = N (z; Eµ, Eσ2 ) and a standard normal distribution N (z; 0, 1) as in a standard variational autoencoder [46, 69], and, (ii) regularizing the latent space with a vector quantization layer by learning a codebook of |Z| different exemplars [96]. To obtain high-fidelity reconstructions we only use a very small regularization for both scenarios, i.e. we either weight the KL term by a factor ∼ 10^−6 or choose a high codebook dimensionality |Z|.

 

The full objective to train the autoencoding model (E, D) reads:

DM Training in Latent Space

Note that for training diffusion models on the learned latent space, we again distinguish two cases when learning p(z) or p(z|y) (Sec. 4.3):

 

(i) For a KL-regularized latent space, we sample

where ε ∼ N (0, 1). 

 

When rescaling the latent, we estimate the component-wise variance

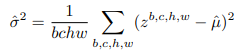
from the first batch in the data, where

 

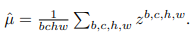
The output of E is scaled such that the rescaled latent has unit standard deviation, i.e.

 

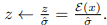
(ii) For a VQ-regularized latent space, we extract z before the quantization layer and absorb the quantization operation into the decoder, i.e. it can be interpreted as the first layer of D.

---