[Lecture 1] Introduction - Reinforcement Learning

https://storage.googleapis.com/deepmind-media/UCL%20x%20DeepMind%202021/Lecture%201%20-%20introduction.pdf

https://www.youtube.com/watch?v=TCCjZe0y4Qc&list=PLqYmG7hTraZDVH599EItlEWsUOsJbAodm&index=1

 

http://incompleteideas.net/book/the-book-2nd.html

---

You are subjected to some data or experience, but the experience is not fully out of your control. The actions that you take might influence the experience that you get.

---

An agent interacting with an environment. The agent executes actions and observes the environment. 

 

The main purpose of this course is then, to go inside that agent and figure out how we could build learning algorithms that can help that agent learn to interact better. And what does better mean, the agent is going to try to optimize some reward signal. This is how we're going to specify the goal. And the goal is not to optimize the immediate reward. We're interested in optimizing the sum of rewards into the future. 

---

 

---

---

---

---

---

---

The expectation depends on the dynamics of the world but also the policy that the agent is following. And then, the goal is to maximize the values we want to pick actions such that this value becomes large. So one way to think about that is that rewards and values together define the utility of states and actions.

 

There's no supervised feedback, so we're not saying this action is correct, that action is wrong, instead, we're saying this sequence of actions has this value, that sequence of actions has that value, and then maybe pick the one that has the highest value conveniently. This is used in many algorithms.

---

---

The value function of states and actions defined as the expected return conditioned on being in that state and then taking that action a.

---

---

Every time step, there's an observation that comes in, and then there's some internal state of the agent and, from the state, the agent might make predictions and it should define some policy somehow. And then, the action gets selected by this policy. 

 

The Agent State refers to everything that the agent takes along with it from one time to the next. 

---

---

An important concept to keep in mind then is that we can also formulate the whole interaction sequence into something that we could call the history of the agent and this is everything that the agent could have observed so far so that includes the observation from the environment but also the actions that the agent took and the rewards that it received. 

 

So this is just taking that interface and storing everything that happens on the interface level. And we could call that the history of the agent. So for instance, it could be the fulll sensory motor stream of the robot.

 

Now we can say that the history is the only thing that can be used to construct the Agent State in some sense. Everything else must be a funciton of your history. There's nothing else essentially the agent has no additional information apart from its sensory motor stream. So that's what you should be using to construct your agent state. 

---

In the full observable case, you can just look at your observation, you could say that tells me everything I need to know about the environment, so I don't need to log any of the previous interactions.

---

A process is Markovian or a state is markovian for this process if the probability of a reward and a subsequent state doesn't change if we add more history.

 

The probability of a reward and a state occuring on time of t+1 conditioned on state St is equal to conditioned on the full history up to that time step. That means the state contains all you need to know, so we don't need to store anything else from the history. 

---

---

The state at your next time step t+1 is some function of your previous state, the action that you've taken, the reward you've seen and the observation that you've seen. So we're taking one step in this interaction loop and we're saying we're going to update the state to be aware of this new time step. 

 

We want this agent update function to give us some compression of the full history maybe recursively and maybe the state actually stays the same size. So St could be of a certain size we see new action, reward and observation and we condense all of the information together into something that is the same size as St.

---

---

---

---

---

If the agent can't distinguish between these two, if it would be using the observation as its full agent state and its action selection policy must depend on only that observation, then it's unclear what it should be doing. There's no single policy, single function of this observation that will do the right thing in both cases. 

 

This is why it can be problematic to not have a Markovian state observation.

---

---

---

Policy pi denotes the probability of an action given a state. 

---

---

The value function depends on the policy, and the way to reason about this, if I have this conditioning on pi means that I could write this long form to say that every action at subsequent time steps is selected according to this policy pi. So note that we're not conditioning on a sequence of actions, conditioning on a "function" that is allowed to look at the states that we encounter and then pick an action.

 

If your discount factor is small or in a special case if it's zero then you only care about the near term future. If you don't want to optimize your policy, then the policy would also be a myopic policy, a short-sighted policy which only cares about immediate reward.

 

Conversely the other extreme would be when the discount factor is one, this is sometimes called the undiscounted case, because then the dicounts disappear from the value definition, where all rewards are equally important not just the first one but the second one also is equally important the first one and that also means that you no longer care in which order you receive these rewards.

 

We can use value function to select between actions. Note we've defined the value function as a function of a policy but then if we have a value function or estimated value function, we can then use that to determine a new policy. You can think of this as kind of being an incremental learning system where you first estimate the value of a policy and then you improve your policy by picking better policies according to these values.

---

The value of a state can be defined as the expected value of the immediate reward plus the discounted value at the future state for that same policy. 

 

V* the optimal value of state S is equal to the maximization over actions of the expected reward plus discounted next value conditioned on that state and action. Importantly, this does not depend on any policy. It just depends on the state. 

---

If you have an accurate value function, then we can behave optimally. If we have a fully accurate value function because then you can just look at the value function, and then the optimal policy could just be picking the optimal action according to those values. So if we have a fully accurate value function, we can use that to construct an optimal policy. 

 

This is why these value functions are important but if we have a suitable approximation which might not be optimal might not be perfect it might still be possible to behave very well even in intractably large domains.

---

---

A model here refers to a dynamics model of the environment. In reinforcement, when we say, we have a model, typically means, a model of the world in some sense. So that means the model predicts what the environment will do next. 

---

---

---

---

---

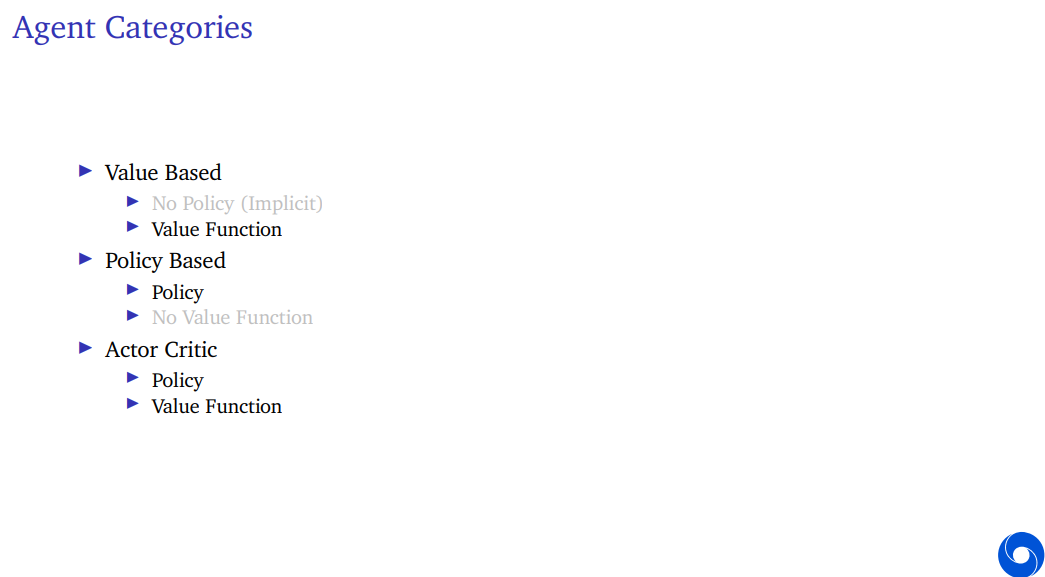
* ActorCritic

Actor Critic refers to an agent which has both an explicit representation of policy and an explicit representation of a value function. 

 

These are called Actor Critics because the actor refers to the policy part. There's some part of the agent that acts and the value function is then typically used to update that policy in some way. So this is an interpreted as a critic that critiques the actions that the policies takes and helps it select better policies over time.

---

---

Prediction is about evaluating the future, for instance learning a value function you could call a prediction problem. And when we say prediction we mean for a given policy. For instance you could think about predicting the value of the uniformly random policy. 

 

Conversely, control is about optimizing the future, finding the best policy. 

 

If we have good predictions, then we can use that to pick new policies. The definition of the optimal policy Pi* is the argmax of policies over these value functions. The value function defines the ranking on policies, your preferernce on policies.

---

There's two different parts to the reinforcement learning problem. One is about learning. And this is the common setting which we assume where the environment is initialy unknown and the agent interacts with the environment and someone has to learn whether it's learning a value function a policy or a model all of that could be put under the header of learning.

 

And then separately we could talk about planning. So planning is typically about when you have a model so let's say the model of the environment is just given to you and then the agent somehow figures out how best to optimize that problem. That would be planning. So that means you're using some compute to infer from the statement of the problem from the model is given, what the best thing to be done is. 

 

Learning refers to absorbing new experiences from this interaction loop and planning is something that sits internally inside the agent's head, it's a purely computational process.

 

Planning is any computational process that helps you improve your policies or predictions inside the agent without looking at new experience. 

 

Learning is the part that looks at a new experience that takes in your experience and somehow condenses that and planning is the part that does the additional compute that maybe turns in a model that you've learned into a new policy.

---

Policies map states to actions or to probabilities over actions.

Value functions map states to expected rewards or to probabilities of these.

Models map states to states or state actions to states.

Rewards map states to rewards or distributions over these.

State update function takes a state and an observation and potentially an action and an reward and maps it to a sebsequent state.

---

---

---

---

---