code example (3): Independence assumption

https://mixtape.scunning.com/04-potential_outcomes#physical-randomization

---

 

Simple difference in means decomposition

---

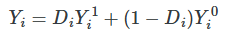
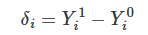
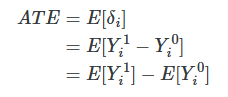
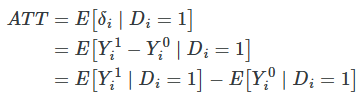
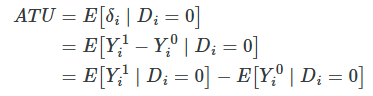
It’s biased because the individuals units were optimally sorting into their best treatment option, creating fundamental differences between treatment and control group that are a direct function of the potential outcomes themselves. 

---

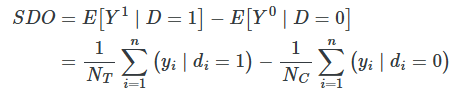
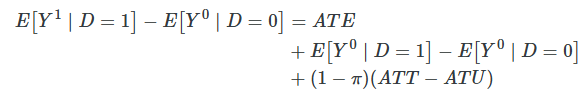
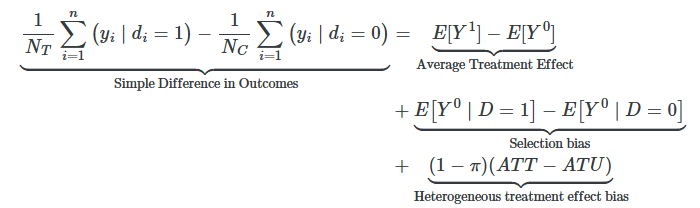
Independence assumption

---

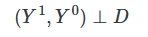
If treatment is randomly assigned, (i.e. independent of the potential outcomes), then the Selection bias and Heterogeneous treatment effect bias zero out, so Simple difference in outcomes equals to Average Treatment Effect.

---

---

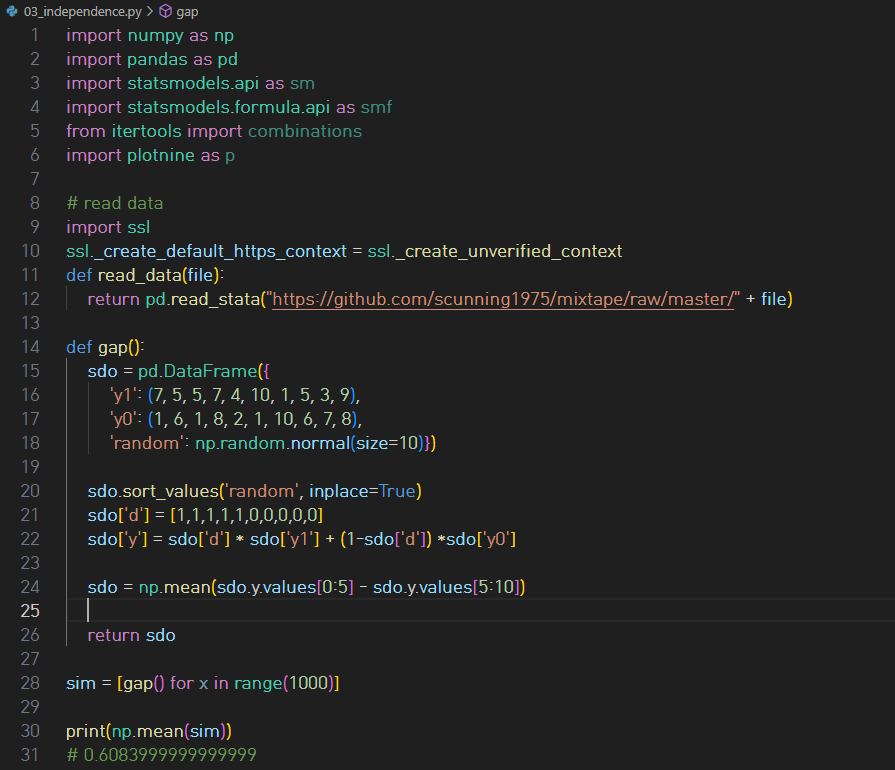
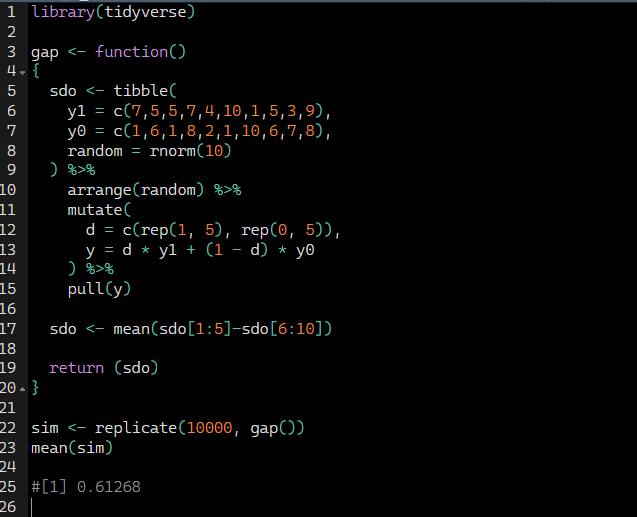
This Monte Carlo runs 10,000 times, each time calculating the average DSO under independence - which is ensured by the random number sorting that occurs. In my running of this program, the ATE is 0.6, and the SDO is on average equal to 0.5988.

 

How realistic is independence in observational data?

 

People are choosing their interventions, and most likely their decisions are related to the potential outcomes, which makes simple comparisons improper. Rational choice is always pushing against the indepencence assumption, and therefore simple comparison in means will not approximate the true causal effect. We need unit randomization for simple comparisons to help us understand the causal effects at play.

---