code example (5): subclassification

https://mixtape.scunning.com/05-matching_and_subclassification

---

Insofar as there exists a conditioning strategy that will satisfy the backdoor criterion, then you can use that strategy to identify some causal effect. We now discuss three different kinds of conditioning strategies. They are subclassification, exact matching, and approximate matching.

Subclassification is a method of satisfying the backdoor criterion by weighting differences in means by strata-specific weights. These strata-specific weights will, in turn, adjust the differences in means so that their distribution by strata is the same as that of the counterfactual’s strata. This method implicitly achieves distributional balance between the treatment and control in terms of that known, observable confounder. 

One of the concepts threaded through this chapter is the conditional independence assumption, or CIA. Sometimes we know that randomization occurred only conditional on some observable characteristics.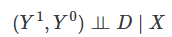

 

The expected values of Y1 and Y0 are equal for treatment and control group for each value of X.

 

Thinking about the simple difference in means decomposition from earlier, we know that contrasting the incidence of lung cancer between smokers and non-smokers will be biased in observational data if the independence assumption does not hold. And because smoking is endogenous—that is, people choose to smoke—it’s entirely possible that smokers differed from the non-smokers in ways that were directly related to the incidence of lung cancer.

 

Probably most damning, though, was the hypothesis that there existed an unobservable genetic element that both caused people to smoke and independently caused people to develop lung cancer. This confounder meant that smokers and non-smokers differed from one another in ways that were directly related to their potential outcomes, and thus independence did not hold. 

 

The connection between the independence assumption and the characteristics of the groups is called balance.

 

If the means of the covariates are the same for each group, then we say those covariates are balanced and the two groups are exchangeable with respect to those covariates.

 

This kind of adjustment raises a question—which variable(s) should we use for adjustment? First, recall what we’ve emphasized repeatedly. Both the backdoor criterion and CIA tell us precisely what we need to do. We need to choose a set of variables that satisfy the backdoor criterion. If the backdoor criterion is met, then all backdoor paths are closed, and if all backdoor paths are closed, then CIA is achieved. We call such a variable the covariate. A covariate is usually a random variable assigned to the individual units prior to treatment. This is sometimes also called exogenous. Harkening back to our DAG chapter, this variable must not be a collider as well. A variable is exogenous with respect to D if the value of X does not depend on the value of D. Oftentimes, though not always and not necessarily, this variable will be time-invariant, such as race. Thus, when trying to adjust for a confounder using subclassification, rely on a credible DAG to help guide the selection of variables. Remember—your goal is to meet the backdoor criterion.

 

In order to estimate a causal effect when there is a confounder, we need (1) CIA and (2) the probability of treatment to be between 0 and 1 for each strata. More formally,

 

These two assumptions yield the following identity

 

where each value of Y is determined by the switching equation. Given common support, we get the following estimator:

---

Imagine that we wanted to know whether or not being seated in first class made someone more likely to survive. But the problem was that women and children were explicitly given priority for boarding the scarce lifeboats. If women and children were more likely to be seated in first class, then maybe differences in survival by first class is simply picking up the effect of that social norm. Perhaps a DAG might help us here, as a DAG can help us outline the sufficient conditions for identifying the causal effect of first class on survival.

Now before we commence, let’s review what this DAG is telling us. This says that being a female made you more likely to be in first class but also made you more likely to survive because lifeboats were more likely to be allocated to women. Furthermore, being a child made you more likely to be in first class and made you more likely to survive. Finally, there are no other confounders, observed or unobserved.

 

Here we have one direct path (the causal effect) between first class (D) and survival (Y) and that’s D→Y. But, we have two backdoor paths. One travels through the variable Child (C): D←C→Y; the other travels through the variable Woman (W): D←W→Y. Fortunately for us, our data includes both age and gender, so it is possible to close each backdoor path and therefore satisfy the backdoor criterion. We will use subclassification to do that.

 

A simple difference in mean outcomes (SDO) is a biased estimate of the ATE, since this does not adjust for observable confounders age and gender. So we use subclassification weighting to control for these confounders. Here are the steps that will entail:

1. Stratify the data into four groups: young males, young females, old males, old females.
2. Calculate the difference in survival probabilities for each group.
3. Calculate the number of people in the non-first-class groups and divide by the total number of non-first-class population. These are our strata-specific weights.
4. Calculate the weighted average survival rate using the strata weights.

---

In a finite sample, subclassification becomes less feasible as the number of covariates grows, because as K grows, the data becomes sparse. This is most likely caused by our sample being too small relative to the size of our covariate matrix. We will at some point be missing values, in other words, for those K categories. In small sample, we probably will end up with many cells having missing information. This is called the curse of dimensionality. If sparseness occurs, it means many cells may contain either only treatment units or only control units, but not both. If that happens, we can’t use subclassification, because we do not have common support. And therefore we are left searching for an alternative method to satisfy the backdoor criterion.

---