Ensembling & Mixture of Experts

※ Summaries after taking 「Advanced NLP - Carnegie Mellon University」 course

https://www.youtube.com/watch?v=MueCRSZ3RQ0&list=PL8PYTP1V4I8DZprnWryM4nR8IZl1ZXDjg&index=14

https://phontron.com/class/anlp2024/assets/slides/anlp-14-multimodel.pdf

---

 

Combining multiple models, this is really important and useful if you want to get an extra few points of accuracy, because it's a pretty reliable way to get improvements. 

 

The basic background is that we have many models that exist and the reason why we have many models that exist is, multiple fold. Number one, we could have different model architectures and we could also have different initializations of those model architectures. 

 

So if we initialize a LLaMa architecture, we start out with random 7B parameters and then we get LLaMa 7B for our pre-training or LLaMa 2-7B. We might initalize another model, this could be the same architecture, different architecture, and train it on the same data or different data and get something like Mistral 7B, these are different architectures, we get a different pre-trained model and, we could also make it bigger or smaller, and then after we do that, there's a lot of fine-tuning that goes on according to different strategies. 

 

So we have a variety of architectures, a variety of random initializations of those architecures, a variety of pre-trained models due to pretraining data or base models and then a variety of fine-tuning models. 

 

The reason why this is important is, because when we're combining multiple models together, some of the methods are applicable to completely different models, some of the methods are only applicable to models that share the same architecture and some of them are only applicable to models that share the same initialization and training trajectory. 

 

So I'll try to distinguish between those as we go forward. 

---

 

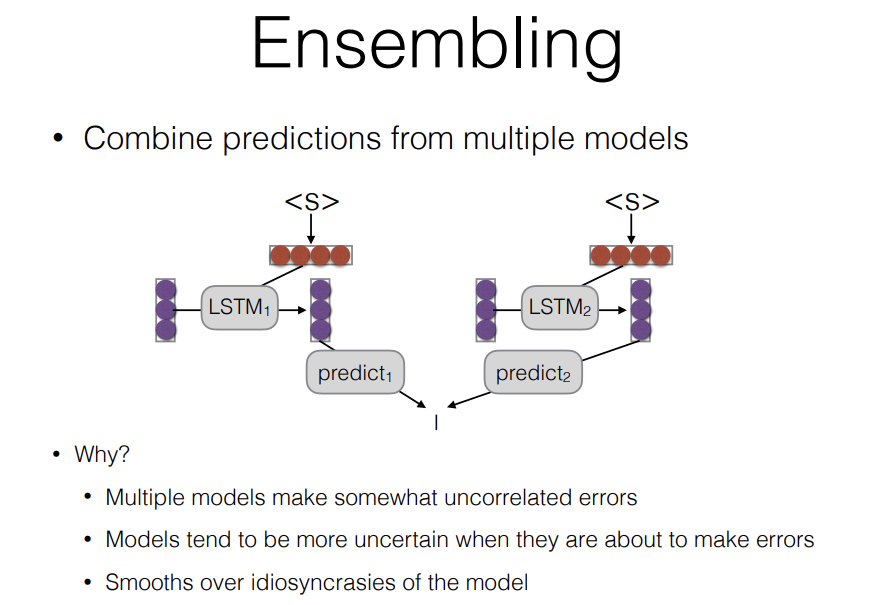
The first thing I'll talk about is model ensembling. Ensembling is a very general technique that you can use in a lot of different ways. But it has its disadvantages as well, so ensembling is combining the predictions from multiple models.

 

Why we want to use two models instead of using one model or just using the best model or in what situation we would want to do this? Number one, it reduces the bias caused by a single model, number two, it's kind of a bayesian perspective, and number three, we have different models and models are better at some things and worse at other things, so errors that models make tend to not be as consistent as when the model is getting it correct. So when you average the two together, you tend to get the right answer more often, because the mistakes that they make tend to less correlated than the probability of getting make that. 

 

And it's because of Smooths over idiosyncrasies of the models, you can even gist Ensemble models from different checkpoints, and that still gives you improvements. When you ensemble models from different checkpoints, it's what data did they see most recently and that also smooths over, the fact that this model happened to see some data more recently, and it's less biased towards doing that.

 

So this is a pretty efffective method, this is one of the few methods that is going to improve my accuracy almost every time. 

---

 

There are two main ways to combine models together, and both of them are useful in different situations. 

 

The first one is, linear interpolation. When you do linear interpolation, what you're doing is, you're taking the weighted average of model probabilities. 

 

This is the probability of the next token according to the model M, and this is the probability of selecting model M. So you talked a little bit about the bayesian approach to this. 

---

The other option is Log-linear interpolation. So linear interpolation, you're taking a linear combination of the probabilities of each model, log-linear interpolation, you're combining together the log probabilities of each model, and then renormalizing, so you get an probabilistic output. What you do is, you have this interpolation coefficient but you're combining together the log probabilities, and here we need to take the softmax. 

 

In linear interpolation, we didn't need to softmax, because probability of model m is gauranteed to be from zero to one, and add up to one and then when you multiply those together, the resulting thing will be between zero and one and add up to one. Here, that's not the case anymore, when we start doing things in log space, because it's not a linear function, so you need to renormalize. 

---

 

Linear vs Log Linear, think of this in logic. What I mean is, linear is kind of a logical OR. It tries to come up with examples where either one of the two assigns a high probability. This can be good at using models that capture different traits or it can also be useful, for example, you have a small model that really captures very specific vocabulary and you want to uppoint that specific vocabulary that gets a really low probability according to a general purpose model.

 

This is also necessary when any model can assign zero probabilities. So if you have an example of vacobulary that isn't included in the vocabulary of another model or you have models with different vocabularies, it's necessary to do this. 

 

Log-linear is more like logical AND. So the interpolated model only likes choices where all the models agree. This is particularly good when you want to restrict possible answers like you want to have one model be able to say no, I really don't like this, so never output it.

 

For example, if you wanted to train a model that was vary adverse to toxic language and prevent the model from outputting toxic language, you could use log-linear model.

---

 

Another thing I should point out is that, we don't necessarily need to use models only as positive evidence. If you're using log-linear interpolation, your interpolation coefficients do not need to be positive, they can also be negative and you can have things where you penalize the probabilities given by a particular model and this has actually been used for a long time. It was actually used in machine translation since 2005 or something like that. 

 

Basic idea is that, you have some models that serve as negative evidence. So you have a core model, this might be your strong general purpose language model, you have a positive model which is the model that you want to boost up and improve and, a negative mdoel which you want to decrease. 

 

One example of this is, a paper that we did in 2019, the core was a machine translation model, and the negative model is an out-of-domain language model, and the positive model is an in-domain language model. So the idea behind this is, a machine translation model you have to train it on machine translation data and machine translation data is not very easy to get for particular domains. For example, you might only have machine translation data in the news domain and you actually want to be doing translation in the medical domain or something, so what you do is, you have your positive model here, this could be a medical domain language model, and this could be a news domain language model. So you're subtracting out the news domain probabilities and adding in medical domain probabilities, move it in that direction.

 

Another example of this is, something called DExperts. The idea here is, you have a strong language model as your core and then as negative, you have a weak toxic language model. So it was trained on lots of bad texts that you don't want to be generating, and the positive is, a weak non-toxic language model that was trained on lots of innocuous posts. So that would help you detoxify the outputs of the language model. So there's lots of examples of things like this that you can do through. 

---

Another thing that I should point out is, there's a lot of other ways to get multiple models. A lot of people are familiar with dropout, it's method for regularizing. It's method for regularizing neural networks or deep learning models in general and the idea is every once in a while, during training, you dropout some portion of the nodes in the neural network model and normally what you do is, at the test time, then you just don't drop out anything and you use the whole neural network model. But another thing you can  do is, at test time, you can drop out five times and combine those different models together through ensembling. That's actually something that people tried in the dropout paper. This is one way to get multiple models and you can demonstrate this helps. The original motivation behind dropout was coming from this idea of ensembling.

 

Another ensembling method that has been around for a very long time is, bagging. The way bagging works is, you have a data and you just resample the data set. So you sample all of the output with replacement and you get another data set of equal size and then you train on this. But you do that like 10 times and you train 10 different models. And then you ensemble those models together. So this is another way to get multiple models. 

 

Both of these still improve your robustness. Because they get a different view on the data. So they smooth over some of the idiosyncrasies. You can also get multiple models from different checkpoints and then put them together.

 

All of these methods are pretty related. What they're doing is, they're taking advantage of the fact that you have particular models that saw different data or saw data in a different order or saw different parts of the data because you dropped out some of the nodes. 

 

And of course, you can also combine together very different models like this (negative evidence) and that also works in different ways.

---

---

The reason why I wanted to mention that dropout is, there's also other efficient methods for using multiple models. The big problem with ensembling is the cost.

 

Simple ensembling is very expensive because it requires you to run multiple models at inference time, and this is something you don't want to be doing if you're deploying a service or something. Because it linearly increases your cost by the amount of models that you're running. It requires both n times of computation and n times of memory. Memory is the worst thing because you need to deploy extra GPU machines.

---

 

So the question is, is there any way we can get some of the benefits of ensembling without having to create multiple models? And luckily the answer is yes.

 

The easiest method for doing so is, something called parameter averaging. What you do is, you just average the parameters of multiple models together. This only works under certain conditions. 

 

What these conditions might be? For different architectures, the parameters could mean different things, and even if the architecture is exactly the same, if your random initialization is different, then that would be a disastrous. Because in neural networks, there's no inherent meaning to like, parameter number one.

 

There's the idea of permutation invariant, which is you could randomly swap all of the dimensions within a neural network and get exactly the same function. 

 

So neural networks have this feature of permutation invariant, so models that were trained from different initializations won't be able to be combined together in this way. 

---

The good thing is actually we have a whole bunch of models that come from the same pre-trained model. So we have this initialization here. This initialization was used to train LLaMa2-7B. Now we have hundreds of models that are derived from LLaMa2. We have hundreds of models that are derived from Mistral. And there, all of the dimensions mean the same thing because they're derived from the same parameters in the first place. So those ones, we can average together. 

---

There's two ways that we can do this. One is by averaging multiple checkpoints during training. So this was the big thing that people did like, you would train model from scratch for a really long time but then you would take the final five checkpoints and you would just average them together. This helps reduce some of the noise that you get from stochastic gradient descent and can improve your overall accuracy, if you're fine-tuning any models, this is something you can do also, because you're probably going to be saving checkpoints, you can just take the best five checkpoints and average them together, and that actually can improve your accuracy quite a bit. 

 

Another thing is, fine-tuned model merging. so fine-tune in several ways, and then merge them together. For example, we might take LLaMa2-7B instruct and Vicuna-7B-1.5 and merge them together with some weights, and we could smooth over their idiosyncrasies and get better results too.

---

There's a few recent papers on this. Previous method (parameter averaging) has been around for a long time since at least 1996, but recently people have examined it a lot in the context of modern networks and this paper Model Soups examines two strategies.

 

The first one is, uniform averaging, where you just average all the parameters together like as you would expect, but they also have a greedy averaging method. And what they do here is, they add one model and check if the whole averaged model improves, and then only if the whole averaged model improves, do they keep that model. Otherwise, they throw it out and then they don't use it. 

 

So what they demonstrate this is, the purple star is when they use greedy averaging, and the blue circle is when they use the uniform averaging and the green is all of the models that they put into this average. What they found is, this is average accuracy on ImageNet, which is the thing that they used in deciding which models to merge in greedily, and then this is on distribution shifts, so on other datasets, other than the ones they use specifically for training. And what you can see is, the greedy averaging method does better than the best single model on the dataset that they used to decide that greedy average. The uniform averaging actually does worse than the best model. 

 

So you would be better off for ImageNet accuracy to just use the best model but uniform averaging is more robust on the distribution shift. 

 

They also demonstrate that averaging is correlated with ensembling. This is ImageNet accuracy of the parameter averaging model, this is ImageNet accuracy of the ensemble. What it shows that, there's a strong correlation between the two. Averaging is almost never better than ensembling the two together.

 

It's faster of course, so it's better because it's faster. There are situations where the ensemble is much better than the average model, so the averaging hurts, ensembling does not hurt. So what this shows you is, parameter averaging is safe and it nearly approximates model ensembling most of the time, but there are cases where it doesn't. So you do need to be a little bit careful and it might hurt your accuracy in some cases. 

---

Previously, we are just merging together two models by taking the parameters of the models and averaging them together. Task vectors and other related works specifically take advantages of the fact that we're looking at different fine-tuned models so, these are models where we have a base model and we know that we fine-tuned from this base model and the basic idea is that, we have our base model here, and the task vector is the difference between the base model parameters and the fine-tuned models parameters. So that's what they define as task vector.

 

What does this allow us to do? This allows us to do a number of interesting things. The first one is that, we can subtract out quote, unquote tasks that we don't want, so let's say, we had a model that was trained on lots of toxic text or we had a model that was trained on lots of private text or something like that, we could subtract out the task vector from this and attempt to remove the model's ability to do that sort of things. 

 

You can also take two task vectors and combine them together like get the model from the combination of the two. This isn't exactly the same as averaging the parameters, because if you average the parameters, you would probably get something in the middle but if you add the two vectors, you would get something different than taking the average, so it gives you a little bit more flexibility about things to do. 

 

(TIES) Another thing this allows you to do is, this allows you to try to resolve confilcts between vectors of different tasks. This has three tasks. It has model one, model two, model three, and each of them has vectors and you'll see that in some cases, these vectors conflict, so we have pink going up, yellow and purple going down, we have yellow going up, pink and purple going down etc etc. What this does is, this identifies the vectors that are pointing the most strongly in particular directions and then it resolves conflicts between them, and comes up with a vector that tries to move in a direction that improves all of the tasks at the same time. 

 

They demonstrate that this is better method for improving the ability to do all of the tasks compared to just averaging things together.

 

--------> 너무 generalist를 만드는 거 아닌감유..? 특정 task에서 잘 하기 위해 fine-tuning을 하는 건데.. 그럼 그 task 쪽으로 parameter가 옮겨가는 게 맞지 않나..? 그 차이(task vector)를 모든 task를 잘 하는 쪽으로 옮겨가겠다는 건.. 흠. 모난 돌이 정 맞는다는 속담이 생각나네.. -_-;; 두루두루 잘 해야 정을 안 맞는 건감유..? ;;

---

There's a popular toolkit called mergekit that makes it relatively easy to do this. It implements a lot of the methods that I talked about here, including the linear methods, the task arithmetic method, and TIES. There is a expansion on this, so if you want to merge together models, it's really easy to do from a software standpoint. 

---

Another simple thing is, distilling ensembles. We already talked about distillation. The idea is simple. You saw parameter averaging only works for same models with the same run. Same model architecture, same initialization. So knowledge distillation trains a model to copy the ensemble and so it tries to match the distribution over the predicted words for an ensemble. and so this allows the model to make the same good predictions as the ensemble, make the same bad predictions as the ensemble. It just allows you to learn more efficiently like distillation does in general. 

---

---

I'll move on to sparse mixture of experts models. This is really important. This is used in a lot of modern models. It's allegedly used in GPT4 and it is definitely used in Mistral which is one of the state-of-the-art open models. 

 

What these do is, they take advantage of sparse computation. So if you think about what happens when you do a scalar tensor multiply where the scalar is zero and the result of the entire resulting tensor is guaranteed to be zero and so you don't even need to do the computation, you don't need to even bother. So, this manifests itself in a bunch of different places in modern models. 

 

The first one could be single rows in a matrix multiply. So if you have a big matrix multiply or big matrix vector multiply, and some of the rows are zero then, that's one place where it happens. You can also do this between zero and in not just rows but also larger tensors and you can even do it in whole models in an ensemble. 

 

So the first one (single rows in matrix multiply) this can be optimzied automatically by GPU. The second one, this often occurs in sparse mixture of experts models and the final one, basically you just don't need to even use the model in ensemble so if you somehow optimize an ensemble, and it turns out that the probability of one of the models is zero, you just can throw it out and not use it at all. 

---

GPU-level sparsity, NVIDIA GPUs support a bunch of different types of sparsity. There's a library called "cuSPARSE" and this is used in PyTorch. 

 

Just to give an example, a vector matrix multiply with sparse vector, such as one that comes from a ReLU activation, what happens is, let's say, you only have three parts of this vector that are active, you just don't need to calculate any of the columns here. So that makes you life relatively easy. 

---

Specific thing that I wanted to talk about is Sparsely Gated Mixture of Experts Layer, because this is what is used in Mistral and probably the GPT models as well. You have a feed forward network and normally a feed forwatd network in Transformer is really wide thing. This huge wide feed forward network that you use to extract a whole bunch of features at each layer and that's where a lot of the computation in Transformer happens.

 

What sparsely gated mixture of experts layer do is, they first have this gating network here where it calculates mixture probability but the mixture probability is zero for many or most of the parts of this feed forward network. So for the ones where it's zero, you just don't calculate it and then, when you mix them together, you use the mixture rates.

 

This is really simple. It's several lines of PyTorch code. The basic idea here is, you have this gating function where you calculate the gating function based on the input and then, you have this keep top K operation and then, you take the softmax over this. The keep top K operation is if the value is wthin the top K, you just keep it and if it's not in the top K, you don't keep it. So that's all. 

 

What's great about this is, then you don't have to calculate many of them. For example, if you keep the top two out of eight, you reduce your computation by four times for this part. 

---

---

Pipeline systems are systems where we have models that the output of one model becomes the input of another model. 

 

To give an example of this, a cascaded system is a system like this, where you take the output of one system and then you feed it into the inputs of another system. So a very stereotypical example of this is, speech translation where you run speech and then you do speech recognition into text and then text you do machine translation into another language. One of the frustrating things about speech translation is, these systems are stubbornly better for a long time than many systems that try to do end-to-end like speech to text in another language. 

 

There's a couple reasons for this. Data availability is way better for speech to text in the same language and text to text in another language than it is for speech to text in another language. Because there aren't large datasets that have speech and text in many languages, so there's a bunch of tricks that you can do to fix this. But still it's tricky and there's a couple other reasons. 

 

Another reason is, speech to text in the same language is just a much more straightforward task and so it's a bit easier to learn. Another thing is, interpretability. And the reason why interpretability is important is, if I'm talking to you in a different language, I'm talking to you through a speech translation system, I want to know if the speech recognition worked because I know if the speech recognition didn't work, then I'm pretty sure that the translation didn't work either, and I can verify the speech recognition but I can't verify the translation. 

 

So there's other reasons why you might want a cascade system other than just accuracy or other things. 

---

There's another idea of stacking. Stacking is very similar to cascading but it allows you to take two different models for the same task with predictions in different ways.

 

So just taking another example, speech translation model, we would first do speech recognition into let's say English and then, we would do translation. And the input to the translation model would be speech in English and text in English, and we would generate the output in Japanese. So it would take both the speech and the text when it was doing translation.  And that would allow it to, number one, get a second opinion about whether the transcription was correct but also like let's say there was some unique information that only appeared in the speech. 

 

So just to give an example "I read the book" and "I read the book" are both transcribed exactly the same way and they're different translations obviously becuase one is present tense and the other is past tense, so there are examples where adding a cascaded system would lose information and a stackted system would not.

---

 

Another thing is an iterative refinement. This is really interesting because large language models have opened up a whole bunch of possibilities for us in this space. This is like cascading and stacking but it can be done multiple times with the same model. So we have an input, we feed it into the model, we get an output and then, we feed the output back in and gradually refine it and make it better and better. 

 

The first time this was done in neural networks was, through something called Deliberation networks. What they do is, they take in an output and then they just gradually refine it to make it better and better. They used a reinforcement learning algorithm to do this where you generated the output and then improved it.

 

Another thing that's really popular nowadays is diffusion models. The way a diffusion model works is very similar. You start out with nothing and then you gradually make it better and better.

 

The key difference between diliberation networks and diffusion models is, diffusion models, you can train from scratch by noising the input, applying noise to the input in training very efficiently and these are very widely used in image generation.

 

They're not super widely used in text just because regular autoregressive models are so good for text. But there are a few efforts to do that. And then a final one is, self-refine.

 

(※ SELF-REFINE: Iterative Refinement with Self-Feedback)

 

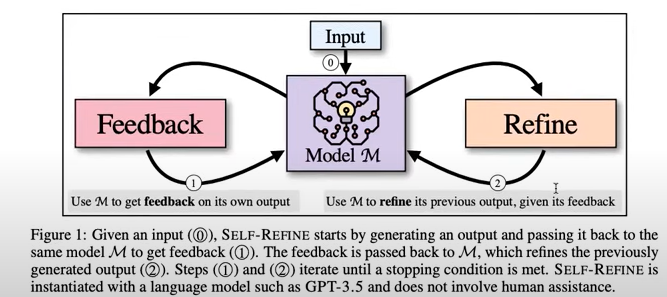
The idea behind self-refine is, what you do is, you feed in the input, you generate an output, and then you ask the model to give you feedback on the output and say yes, this output is good or no, this outout has an error, then you feed in both the output and the feedback back and ask the model to refine its output and you do this over and over again. And this allows you to improve the output. This is has ended up being pretty effective in a pretty wide number of tasks. 

 

One caveat about this is your model has to be really good for this to work. Only models kind of on the level of GPT4 not on the level of GPT3.5 have the ability to do this pretty consistently. So it is something you need to be aware of. 

---