#1 Summaries on Efficient Attentions

(1st version - Sep 14, 2024 @Soyoung, Park) 

Intro

Before dive into the content, I'd like to mention a few things. 

 

First, this is my first attempt to summarize various researches on making Transformer efficient. So it's really hard to cover exhaustively all of the great works that makes transformers efficient. 

 

These works can be categorized in many different ways and moreover, broadly, we can even think about optimization techniques such as lower-precision, quantization, distillation, pruning etc. 

 

However, here, I'd like to focus mainly on "efficient attention" and not cover other methods which optimizing Transformers such as techniques that I mentioned above. 

 

The reason is that, in this article, I'd like to focus on algorithms and models that have "lower complexity" - especially "linear complexity" than the original one. 

 

Second, since there're great studies going on, I'm going to keep updating.

 

Last but not least, the motivation that I write this article is that when I read Mamba-2 paper, I had a strong impression that the authors were trying to encounter attention.

 

Attention and Mamba(SSMs) have different architectures but they boil down to the same concern - the question of how to compress history (context) well to predict output (next token in LLM). 

 

More precisely, How to remember "more" tokens (longer sequences) "better" (more relevant information, context) and reflect them in output (next tokens) "efficiently".

 

I think they have commonalities/differences between each other and can be used as "complementary" to improve performance!

 

I hope to do research on this topic later on. 

 

So, it seems like attention is still dominent backbone of the most of successful AI applications. Then, what's the problem of attention? What made people such excited when Mamba first came out? - "Quadratic complexity". - (attention considers all possible pairs of words within the context window to understand the connections between them, resulting limitation on large context windows).

 

So in this article, I'd like to talk about various approaches that address this issue and make attention efficient - "reducing complexity".

---

source: Sasha Rush's blog

---

Table of Content

1. Sparse Factorization - 「Generating Long Sequences with Sparse Transformers」

2. LSH-Attention - 「Reformer: The Efficient Transformer」

3. 「Efficient Attention: Attention with Linear Complexities」

4. Kernelized Attention - 「Transformers are RNN's: Fast Autoregressive Transformers with Linear Attention」

5. Taylor Approximation - 「Linear Attention Mechanism: An Efficient Attention for Semantic Segmentation」

6. 「Linformer: Self-Attention with Linear Complexity」

7. 「Longformer: the Long-Document Transformer」

8. 「Big Bird: Transformers are Longer Sequences」

 

(Content will be updated continuously)

---

1. Sparse Factorization 

(2019) https://arxiv.org/pdf/1904.10509

 

 

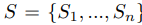
The idea of this paper is based on the fact that the attention matrix is typically sparse, meaning that in each row, only a few tokens have high weights and the rest have weights close to zero. So this paper introduces several sparse factorizations for the attention matrix.

 

In the original attention mechanism, we compute the attention weights for each token attending to all the tokens in the sequence. In factorized attention, we only attend to subset of tokens and thereby compute dot product of queries and keys in that subset only. 

 

This is done by adding Si to the attention equation that defines the connectivity patterns for the i token.

 

With the sparse attention, we can have different connectivity patterns at different heads. For defining the connectivity patterns, it is important to make sure that the signal can be propagated from any position to any other position within a constant number of steps.

 

A sparse attention proposes two schemes to define connectivity patterns. The first scheme is called a strided pattern. If you select any arbitrary positions, i and j, we can reach from i to j with maximum two steps. One step for traversing horizontally and the other step for traversing vertically. 

 

Such a strided sparse attention is suitable for data that have a periodic structure such as images.

 

For other types of data that lack such periodic structure, they define fixed patterns. In this paradigm, we have dedicated positions that summarize information from their previous locations and then propagate it to all future positions. 

 

The complexity of the sparse attention is order of n times the root of n.

---

※ Another design of connectivity pattern: Star-Transformer (https://arxiv.org/pdf/1902.09113)

---

2. LSH-Attention

(2020) https://arxiv.org/pdf/2001.04451

 

Instead of presetting the connectivity patterns, Reformer proposes to determine connectivity patterns using the similarities of queries and keys based on locality sensitive hashing.

 

So the general idea is that, we can use a locality sensitive hasing or LSH to group similar pairs together and define the connectivity patterns among each group. The LSH maps similar points to the same bucket with a high probability while the distant points are placed in different buckets with high probability.

 

For LSH attention, we have to use identical queries and keys. We map each query to a bucket by applying the LSH function. After mapping all the queries to the buckets, we define the connectivity patterns based on these buckets. After obtaining the buckets, we sort these buckets and create chunks of equal size.

 

This algorithm has complexity of order of n log of n. But it is important to note that while the complexity with respect to n is reduced from quadratic to n log of n, there is a large constant c, so LSH attention is only faster when dealing with very long sequences. 

 

Reversible layers: ( A ) In a standard residual network, the activations from each layer are used to update the inputs into the next layer. ( B ) In a reversible network, two sets of activations are maintained, only one of which is updated after each layer. ( C ) This approach enables running the network in reverse in order to recover all intermediate values. source: https://research.google/blog/reformer-the-efficient-transformer/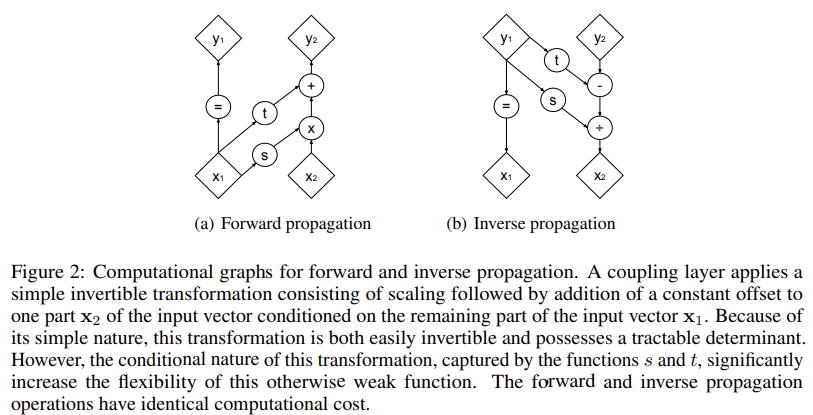

Density Estimation Using Real NVP https://arxiv.org/pdf/1605.08803

 

While LSH solves the problem with attention, there is still a memory issue. When training a multi-layer model with gradient descent, activations from each layer need to be saved for use in the backward pass. A typical Transformer model has a dozen or more layers, so memory quickly runs out if used to cache values from each of those layers.

 

The second novel approach implemented in Reformer is to recompute the input of each layer on-demand during back-propagation, rather than storing it in memory. This is accomplished by using reversible layers, where activations from the last layer of the network are used to recover activations from any intermediate layer, by what amounts to running the network in reverse. In a typical residual network, each layer in the stack keeps adding to vectors that pass through the network. Reversible layers, instead, have two sets of activations for each layer. One follows the standard procedure just described and is progressively updated from one layer to the next, but the other captures only the changes to the first. Thus, to run the network in reverse, one simply subtracts the activations applied at each layer.

---

3. Efficient Attention: Attention with Linear Complexities

(2018) https://arxiv.org/pdf/1812.01243

The general idea of efficient attention is very simple. From linear algebra, authors utilize the associativity of matrix multiplication. 

https://cmsflash.github.io/ai/2019/12/02/efficient-attention.html

 

"After the swapping, the size of the intermediate result changes from n*n to k*c. Since both k and c are constants under our control, the resultant memory complexity is O(1). After some calculation, you can get the computational complexity, which is O(n). This is the efficient attention mechanism."

 

"What about normalization? Since softmax is nonlinear, we cannot simply move the operation to N or another matrix. However, we can approximate its effect with two seperate softmax operations on C and B, respectively. The softmax on C is performed along its channel dimension, while the one on B is along the spatial dimension. After these operations, if we multiply C and B, their product will satisfy the same essential property as M that each row in it sums up to 1. Despite these operations are not exactly equivalent to the original, we have conducted empirical experiments to verify that the approximation doesn’t cause any degradation in performance." (https://cmsflash.github.io/ai/2019/12/02/efficient-attention.html)

https://cmsflash.github.io/ai/2019/12/02/efficient-attention.html

---

4. Kernelized Attention

(2020) https://arxiv.org/pdf/2006.16236

 

This paper also proposed a linear attention mechanism, but with a slight different approach which is based on the kernelized version of attention formulation.

 

"We express the self-attention as a linear dot-product of kernel feature maps and make use of the associativity property of matrix products to reduce the complexity from O(N^2) to O(N), where N is the sequence length. We show that this formulation permits an iterative implementation that dramatically accelerates autoregressive transformers and reveals their relationship to recurrent neural networks. Our linear transformers achieve similar performance to vanilla transformers and they are up to 4000x faster on autoregressive prediction of very long sequences." 

 

"In our paper, we show that replacing the softmax attention with a linear dot product of kernel feature maps ϕ(Q) and ϕ(K) allows us to express any transformer as a recurrent neural network with the following update equations, where xi denotes the i-th input, yi the i-th output and si, zi the hidden state at timestep i"  (https://linear-transformers.com/)

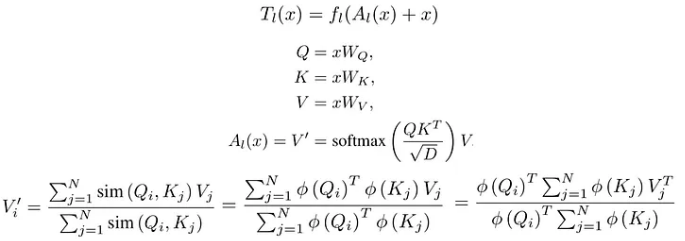
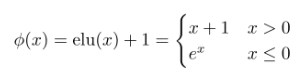
The above formulation allows for efficient autoregressive inference with linear time complexity and constant memory.

---

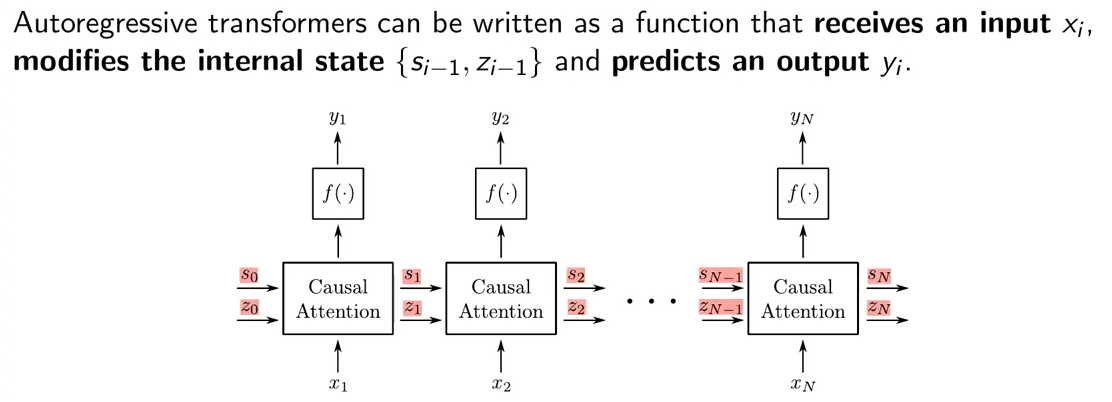
※ Universal Transormer: shares weights in every layer which can be viewed as RNN in depth-wise.

(https://arxiv.org/pdf/1807.03819)

---

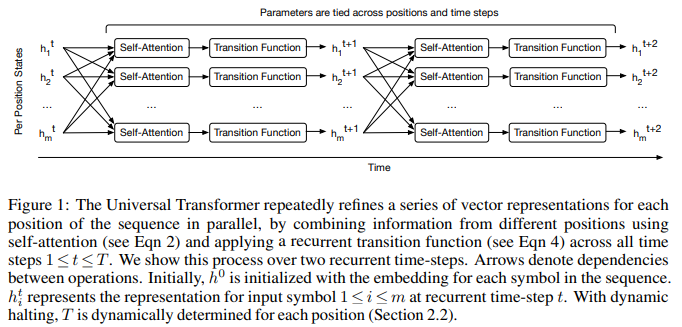
5. Taylor approximation

(2020) https://arxiv.org/pdf/2007.14902

This paper is based on first order Taylor series expansion to derive the attention with linear complexity.

 

"substituting the attention from the conventional softmax attention to first-order approximation of Taylor expansion lead to linear time and memory complexity."

---

6. Linformer

(2020) https://arxiv.org/pdf/2006.04768

 

Linformer is based on the low rank approximation of the attention matrix. So the attention matrix from softmax function is a low rank matrix. 

 

When we describe a matrix A as low rank, it implies that A can be closely approximated by the multiplication of two smaller matrices B and C. And to find these smaller matrices, we can use SVD or singular value decomposition. For example, with A, we can write that as A equals U times sigma times V where U and V contain the left and right singular vectors and sigma is a diagonal matrix with the singular values of A. Then we can take the r largest singular values and their corresponding singular vectors and approximate A.

 

The problem is that SVD by itself is computationally very expensive and the overhead cost of adding SVD will end up hurting rather than helping. So Linformer's attention tries to approximate the low rank attention matrix without explicitly computing the SVD. 

---

"Our approach is inspired by the key observation that self-attention is low rank. More precisely, we show both theoretically and empirically that the stochastic matrix formed by self-attention can be approximated by a low-rank matrix. Empowered by this observation, we introduce a novel mechanism that reduces self-attention to an O(n) operation in both space- and time-complexity: we decompose the original scaled dot-product attention into multiple smaller attentions through linear projections, such that the combination of these operations forms a low-rank factorization of the original attention."

 

"we apply singular value decomposition into P across different layers and different heads of the model, and plot the normalized cumulative singular value averaged over 10k sentences. The results exhibit a clear long-tail spectrum distribution across each layer, head and task. This implies that most of the information of matrix P can be recovered from the first few largest singular values."

 

"In Figure 1 (right), we plot a heatmap of the normalized cumulative singular value at the 128-th largest singular value (out of 512). We observe that the spectrum distribution in higher layers is more skewed than in lower layers, meaning that, in higher layers, more information is concentrated in the largest singular values and the rank of P is lower."

---

7. Longformer

(2020) https://arxiv.org/pdf/2004.05150

Longformer is designed to process long documents like the articles on archive.

 

Longformer's attention uses a combination of local and global attention patterns. For local attention, they use a sliding windows or dilated sliding windows. Capturing local context is very important since a lot of information about a token can be obtained from its neighboring tokens.

 

For global attention, they use some pre-selected tokens and make symmetric attention patterns. Meaning that all other tokens attend to these pre-selected global tokens and these tokens also attend to all other tokens.

 

This way, long range dependency signals can propagate from one position in the input sequence to another location.

 

---

8. BigBird

(2021) https://arxiv.org/pdf/2007.14062

 

Similar to Longformer, BigBird also uses a combination of local and global patterns. But in addition, they also use random patterns as well.

 

The idea of using random patterns comes from graph theory, where starting from a fully connected graph where nodes are tokens and edges represent the connectivity patterns.

 

Then with graph specification, we can randomly drop a large fraction of edges and still maintain a small average path between the nodes.

 

Next, for local attention, a window of size w around position i in the adjacency matrix is set to one. That is cells from i minus w half to i plus w half are set to one.

 

And finally for global attention, they propose two approaches. One is called BigBird-ITC or internal Transformer construction which makes use of the existing tokens for global attention. So a set of pre-selected tokens will attend to everyone and everyone will attend to them.

 

The second approach is called BigBird-ETC or extended Transformer construction where they introduce some additional tokens to the sequence and make everyone attend to them while they also attend to everyone.

 

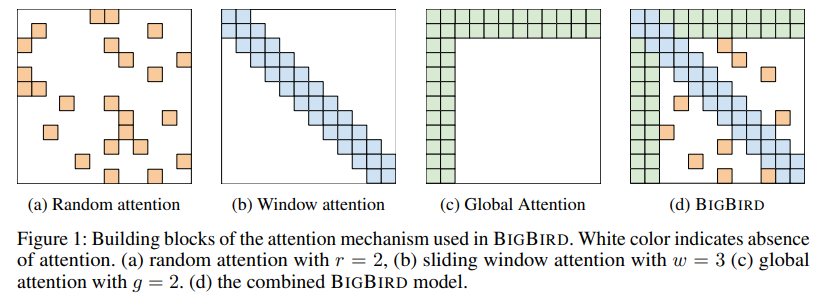
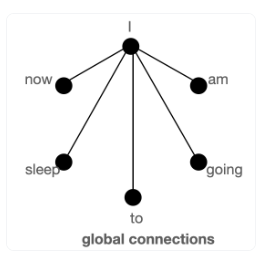
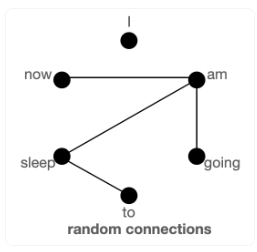
https://huggingface.co/blog/big-bird

---