PPO & RLHF & DPO

https://www.youtube.com/watch?v=SgC6AZss478&list=PLs8w1Cdi-zvYviYYw_V3qe6SINReGF5M-&index=1

https://www.youtube.com/watch?v=TjHH_--7l8g&list=PLs8w1Cdi-zvYviYYw_V3qe6SINReGF5M-&index=2

https://www.youtube.com/watch?v=Z_JUqJBpVOk&list=PLs8w1Cdi-zvYviYYw_V3qe6SINReGF5M-&index=3

https://www.youtube.com/watch?v=k2pD3k1485A&list=PLs8w1Cdi-zvYviYYw_V3qe6SINReGF5M-&index=4

---

---

---

 

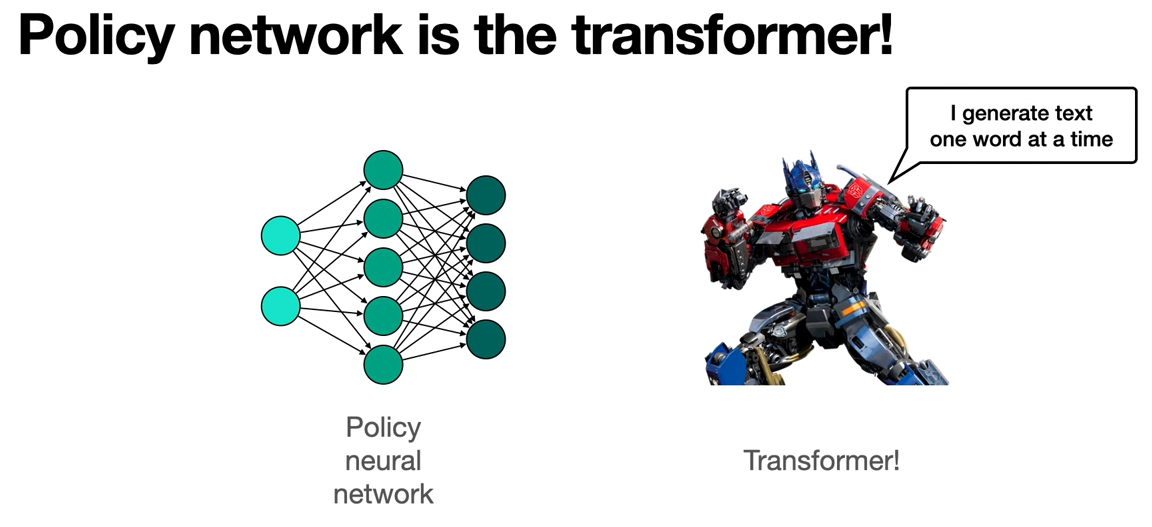
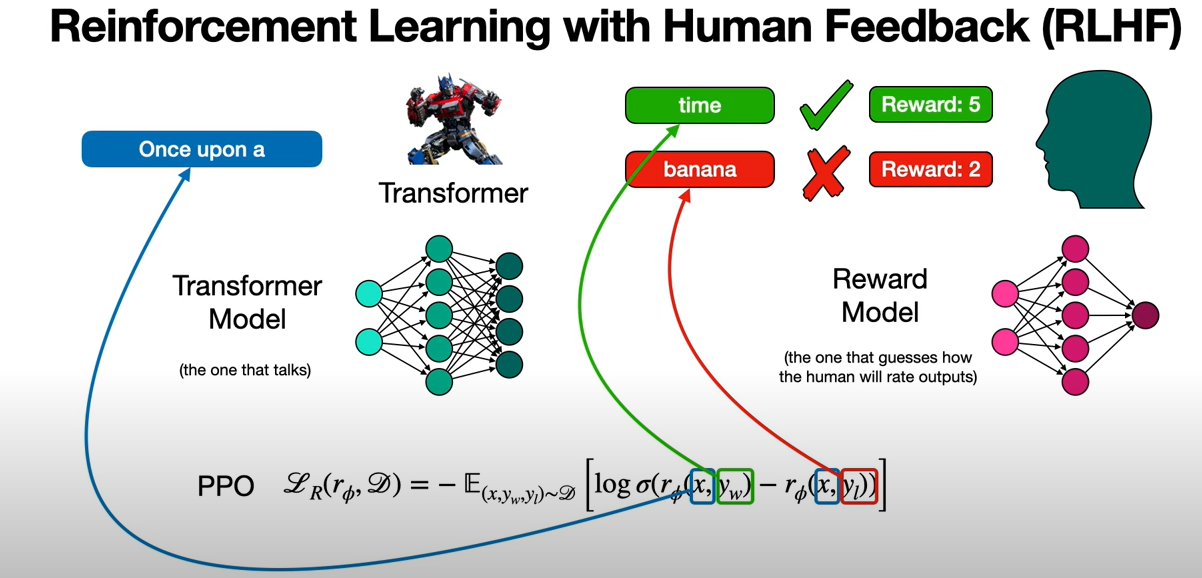
The idea is that, we have a Transformer that we have already trained. So it's already working well and we're going to use some human feedback to improve it. So in order to get the human feedback, we're going to feed it some prompts, for example, "Once upon a" and then, the Transformer's task is, to find the next word.

 

So the next word could be, "time" or could be "banana". Let's say, these are two responses that the Transformer gives, and it's up to a human to decide which one is better.

 

So a human evaluator will say, "well, time is better, because once upon a time is better thatn once upon a banana" and actually the human evaluator will not just say which one's better but it'll actually give some scores. For example, it's going to give a score 5 to the good answer and a score of 2 to the bad answer. 

And, we're going to call scores, rewards. 

 

So how does RLHF work? It has two neural networks. The first one is the policy neural network and the second one is the value neural network. Now from reinforcement learning, it's common to have a policy neural network and a value neural network. This time, they're going to have some very specific tasks. 

 

So the policy neural network is the Transformer model, so this is the one that talks. This is the model that when you input a prompt, it outputs the next word. 

 

And the value neural network is called the reward model. And this one learns to mimic what the human evaluator does. So given a lot of responses by a human, the reward model learns how a human responds, and then it mimics those responses. 

 

Now how do we train these two networks? They help train each other. So it's a cyclical process where one helps train the other one and the other one helps trains the one. 

 

Here is an objective function. In this formula, we have x which is the prompt and then, we have y_w which stands for winning and that's the winning response. And then, y_l which stands for losing which is losing response. Notice that this r refers to the reward model. 

 

However, there's problem with our RLHF which is that, we have to train two neural networks. This is a long process and it may not be very efficient all the time. So we want to do directly. So we're going to do away with our RLHF and we're going to bring Direct Preference Optimization.

---

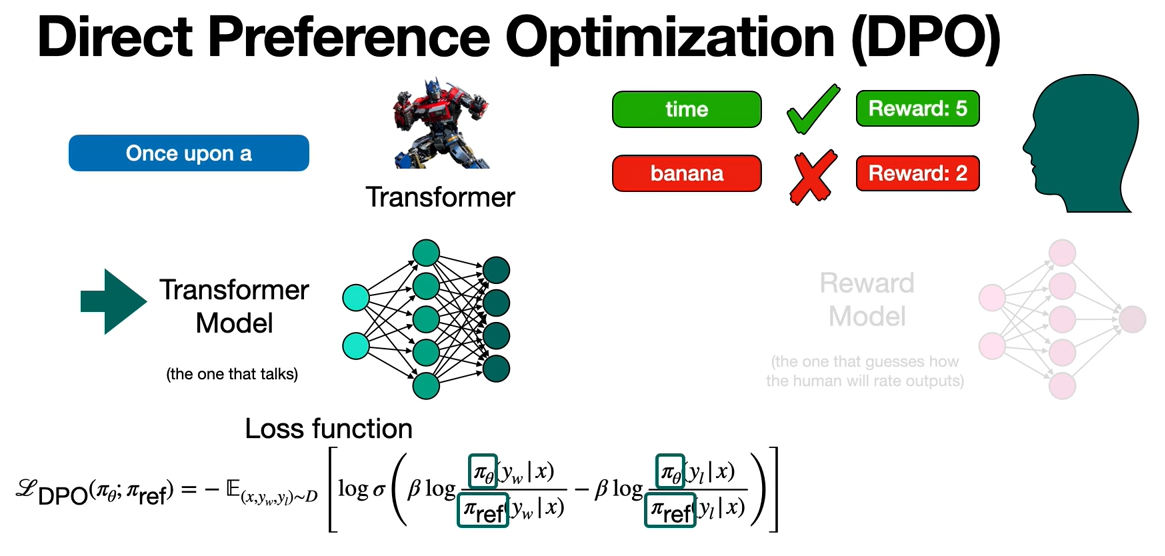
What Direct Preference Optimization does is, it only worries about one neural network that Transformer model. And it kind of doesn't use the reward model, so I'm kind of lying because it doesn't fully forget it. It actually embeds the reward function inside the Transformer model loss function.

 

Here is the loss function of the Transformer model. Notice a few things. This pi is the probability of the response y given the input x. So it's a probability that you would output "time" or output "banana" given that the input is "once upon a". And those pi come from the Transformer model. 

 

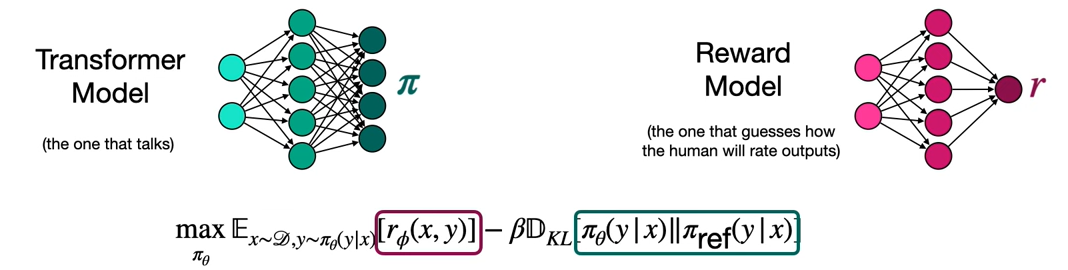
Now I mentioned that, we don't really forget about the reward model. What we do is that, we train the Transformer model with a loss function that includes the reward. And for that, we need a formula that contains the reward and the policy from the Transformer model. And it's this one over here. So this is going to help us get to that loss function. Notice that this formula has the reward over here from the reward model, and the policy over here from the Transformer model. You can think of pi as the probability of the next word. 

---

So let's focus on this formula. It has two main components. The first one is this one which is trying to maximize the rewards because at the end of the day, we want the Transformer neural network to output the words or the responses that have the highest reward. For example, if the input is "Once upon a" and we have "time" and "banana", we want it to output "time". So we want to maximize that reward. So that's the first part of the neural network. 

 

And the second part is this one, what it does is that, it prevents the model from changing too drastically from one iteration to the next. 

---

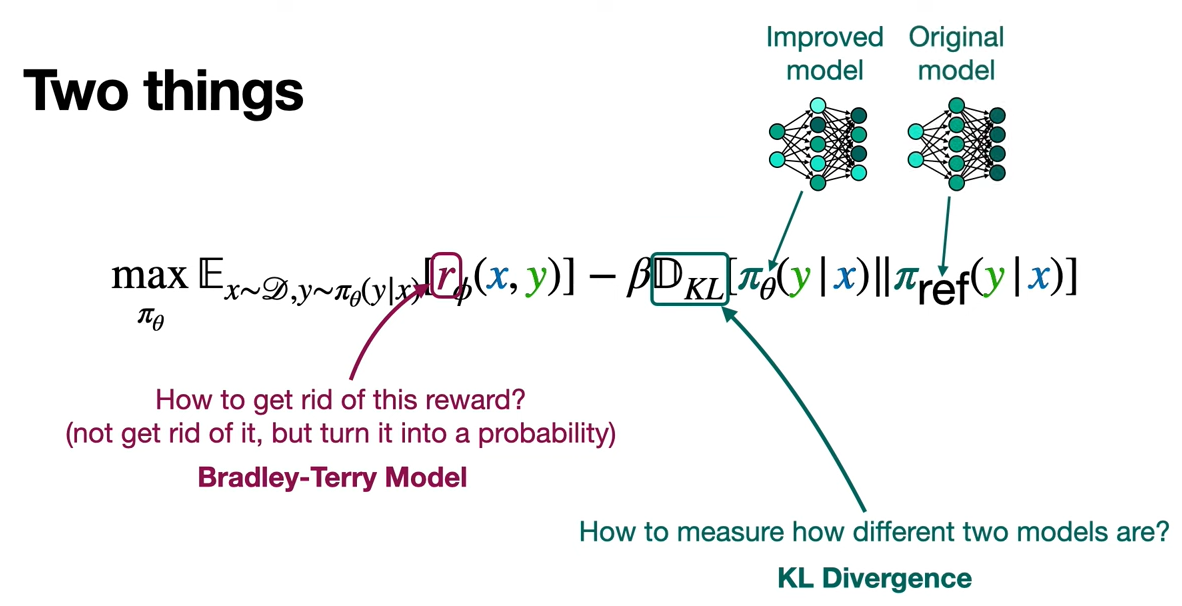
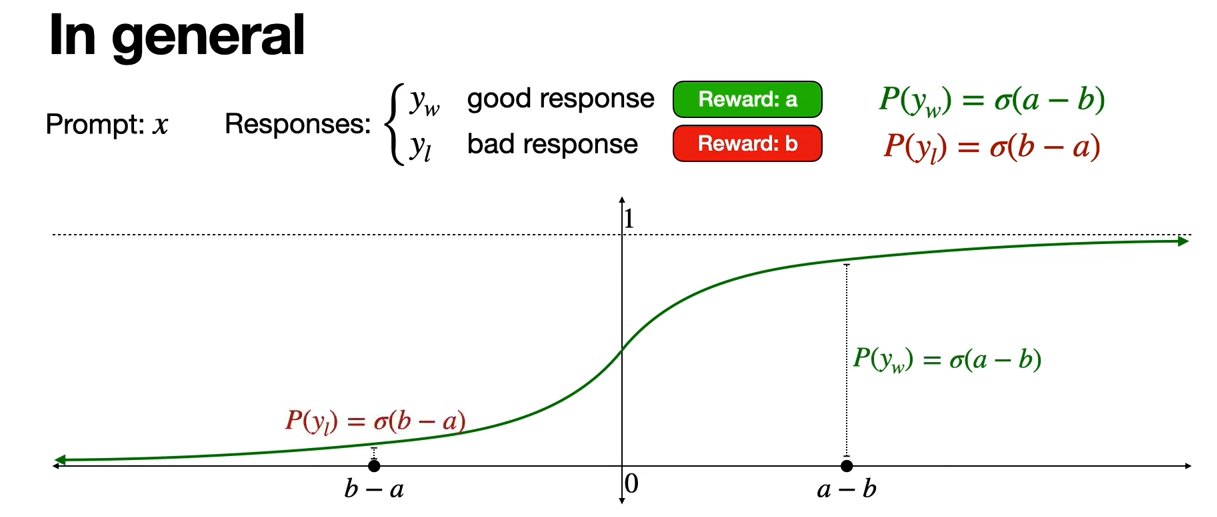
What we want is to get rid of the reward, not get rid of it, but we want to turn it into a probability. So that the loss function only has probabilities, and not rewards. How do we do that? Using something called the Bradley-Terry Model. 

 

And we have something called D_KL, that is a way to measure how different two models are, and that's called KL divergence. What are we comparing? We're comparing that improved model with the original model and what we're doing is, comparing the distributions that these models generate. Because what KL divergence does is, it compares two distributions and it outputs a large number if they're very different and a small number if they're very similar. 

---

Let's look at the Bradley-Terry Model. That is going to trun rewards into probabilities, so that we can rewrite this formula with only pi and not r. 

---

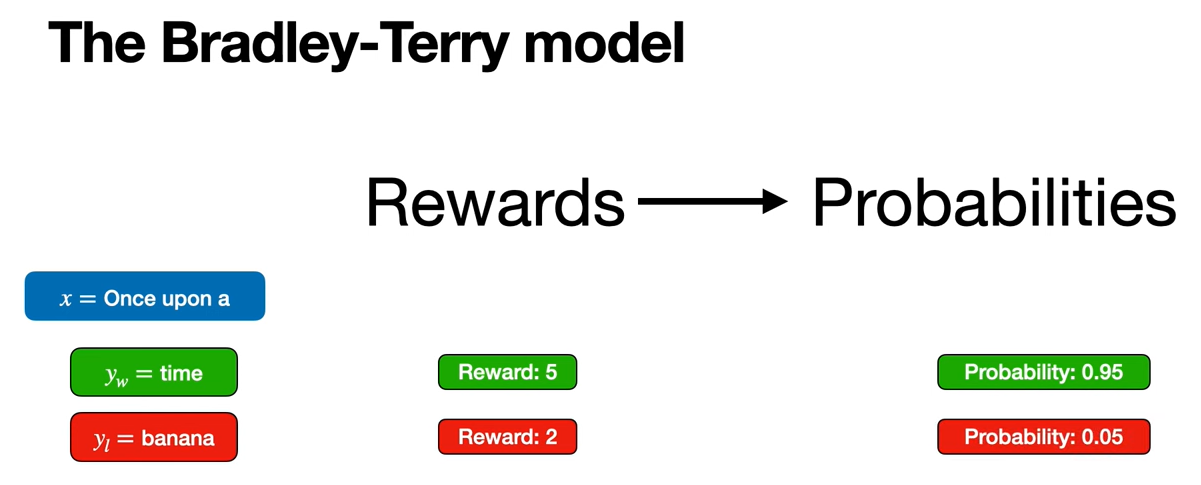
The Bradley-Terry model turns rewards into probabilities. For example, if the input is "once upon a" and the outputs are "time" and "banana", the human evaluator will give them some scores like 5 and 2. But we don't want scores. We want probabilities. So we're going to turn this into the probability of the word "time" is 0.95 and the probability of the word "banana" is 0.05. So I'm going to show you a very simple formula that turns rewards into probabilities. 

---

 

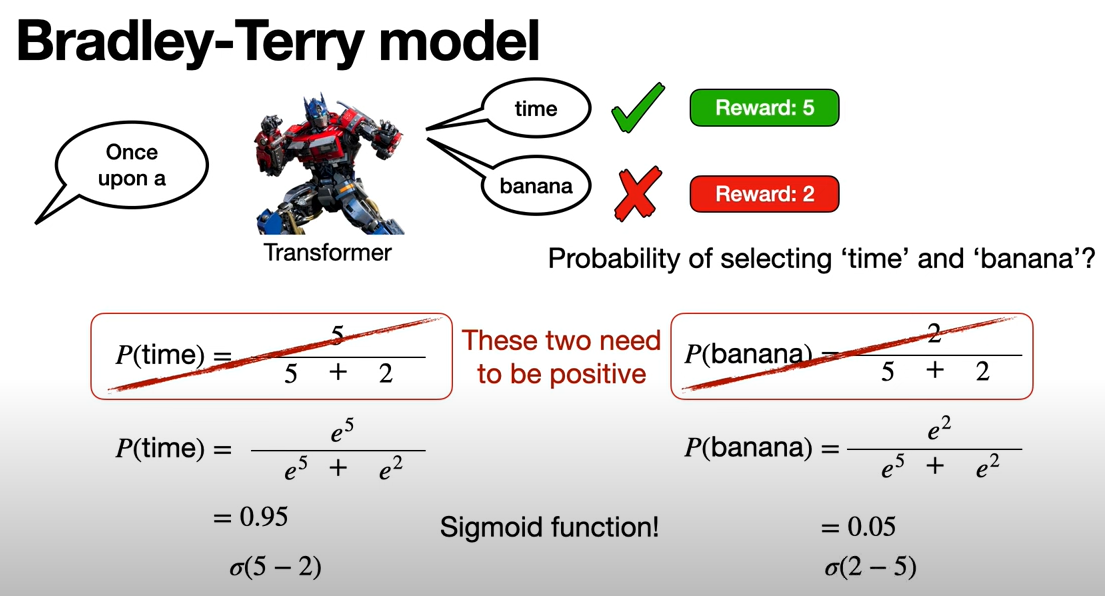
Let's say, we have a Transformer. We give it the input and it outputs two things. The human evaluator says, this one's good, this one's bad and gives them rewards of 5 and 2.

 

So now how would you turn these two scores into probablities? That's what the Bradley-Terry model provides. It provides one good way of turning this scores into probabilities.

 

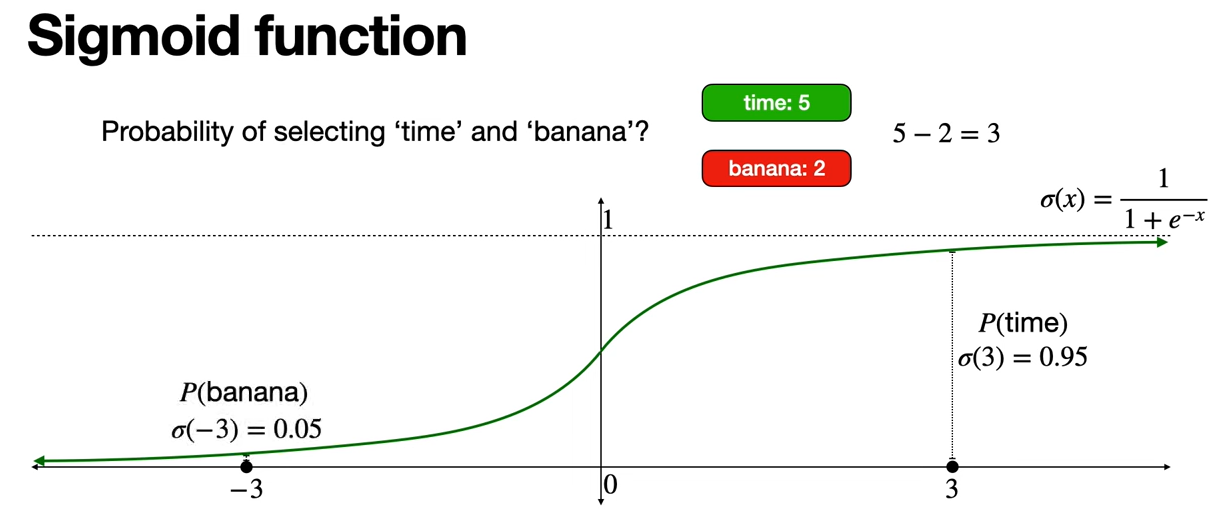
So let's think. How much would P(time) and P(banana) be? We want P(time) to be higher than P(banana), because time has a reward of 5 and banana has a reward of 2. So why don't we make them proportional to 5 and 2. 

 

This is precisely the sigmoid function. 

---

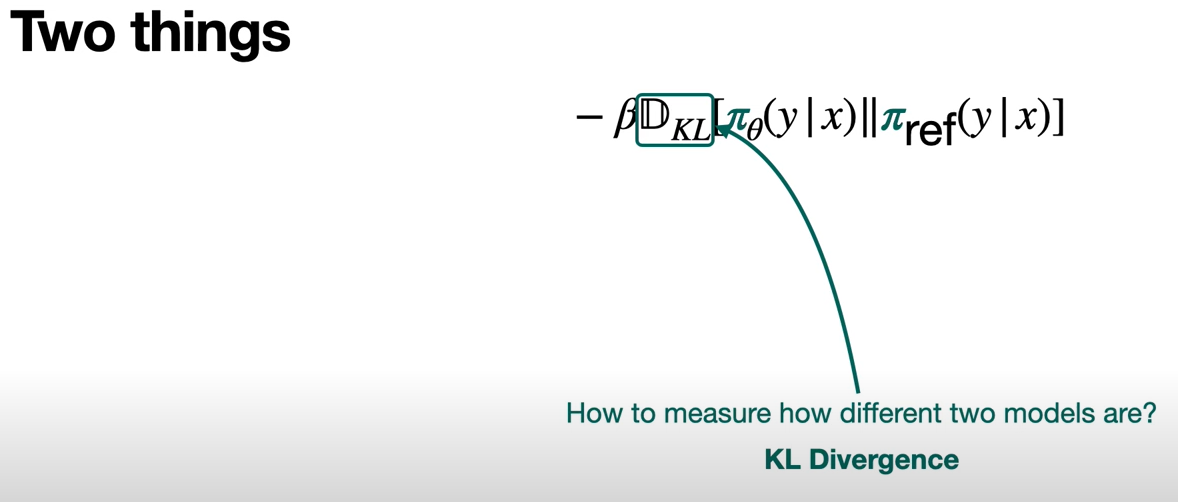
I'm going to tell you why we don't want the model to change too much.

Let's imagine that we are giving our friend a test and so our friend takes the test which has 10 questions and these are their numerical responses. Now our friend has studies a lot and did really well on the tests. So we trust our friend. However, we look at question 7 and we can give our friends some feedback and say, the actual answer for question 7 is this one over here, so you can improve a little bit and so our friend goes and studies a little more and then, comes back with this test which is very similar to the first one. And it does a little better in question 7. So we're happy with that. This is good.

 

But then, our friend says, wait, I did something different. Check this out. And then, it shows us a new set of responses and in here, question 7 is perfect now. The problem is that, in this test, our friend changed the responses very drastically.

 

The first time, our friend did really well. They fixed question 7, but they changed some responses. So now here is a question. Which one of the tests would you trust more? I would go for improved test 1, because even though the test 2 did much better in question 7, it changed everything so much that it may not be trustable. 

 

If the responses were good already, there's no reason to change them drastically. 

 

Now, how do we go for improved test 1? We need a metric for how similar tests are. So the original test and the improved test 1 are very similar, however, the test and the improved test 2 are very dissimilar. 

 

So we need a way to measure how similar these tests are. And that measure is going to be KL Divergence. 

 

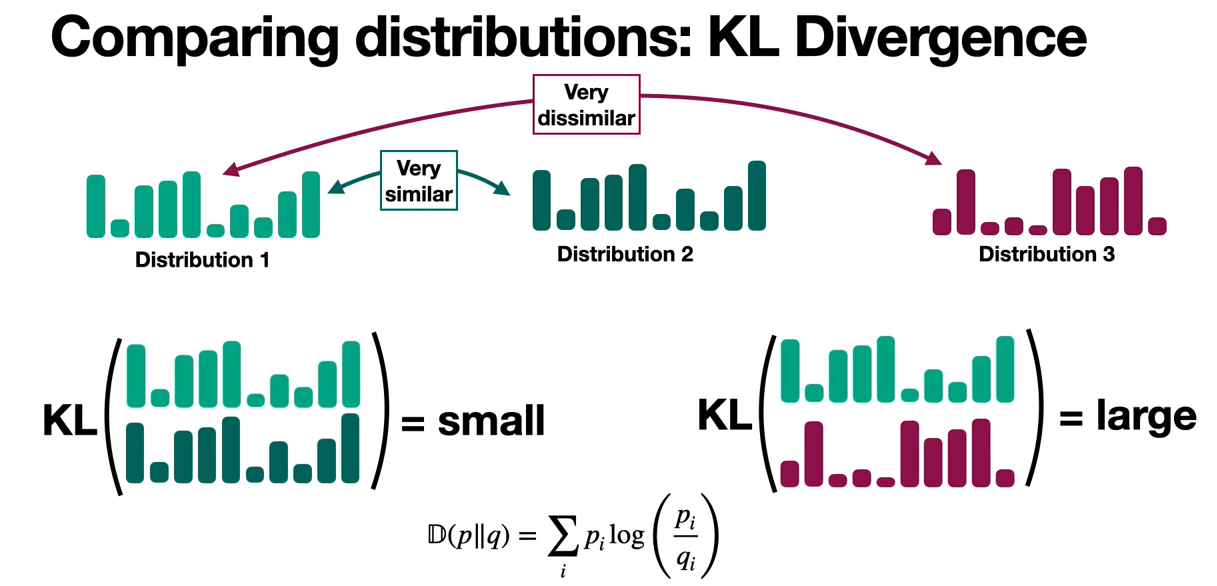
KL Divergence is a way to compare distributions. What KL Divergence does is, it takes a pair of distributions and returns a small number if they're very similar and a large number if they're very different. 

 

We're going to try the grade question 7 in a way that rewards the test that is similar to the original and punishes the test that is different from the original while still grading question 7. So we're going to come up with a modified grade for question 7. 

 

The grade is the grade in question 7 - the divergence with the original test. We're adding the grade in question 7, because we want to make sure the answer improved but we want to subtract the divergence with the original test to punish tests where the answers changed a lot and reward tests where the answers stay similar. 

---

 

And we're going to use the same rationale to find a loss function for a Transformer model. For a Transformer model, we're going to say that, the modified grade is going to be the performance in the new data - the divergence with the previous model. So the performance in the new data is the rewards from the data that we gave it from the new prompts. We want to measure this performance, because we want to make sure the model improved on the data we gave it, that the human evaluator rated. 

 

But we also want to punish the divergence with the previous model, because we want to make sure that the model does similarly on the other data that it doesn't change answers dramatically from others. Because we trust the model, we trust the original model. It's been trained already, so we need to fine-tune it but we don't need to change it drastically. 

---

 

The divergence here is calculated between the Transformer model which is the one we're training and the Transformer model that we started with. Those are the two models we use to calculate the KL Divergence.

 

And what is this Beta? That's a hyperparameter. We can tune that hyperparameter. This hyperparameter tells us, if we want to punish the change a lot or if we want to punish it very little. In other words, if we really don't want the model to change or if we're going to allow it to change a little bit in order to improve the answers. 

---

 

Now we're almost getting to the Loss function. Because we have our function which maximizes rewards and punishes when the model changes too much, and then we also have the Bradley Terry Model which turns a reward into a probability. Now what they did in the paper is, they put this together, did a lot of mathematical manipulation and out came the loss function.

 

Notice one thing that, this loss function does not have the letter r on it, and that's what we wanted. Because we didn't want the reward to be there directly. Because we don't want to be training our reward neural network. Now the r is there implicitly but thanks to the Bradley Terry model, it has been turned into a probability.

---

 

Now we can look at this loss function and say, it just came out of those other formulas. It's a mathematical manipulation that came out of those. And unfortunately that seems to be the big thing about this formula that it came out of the other three. However, we can still look at some things in this loss function that makes sense.

 

For example, we have the probability of the winning response, given x is the input. That means, we are maximizing the probability of a good response. 

 

Here is the probability the model gives to the bad response y_l given the input x, and want to minimize this reward. Why do we minimize? Because we have a minus sign here, so we're subtracting it. 

 

Notice that, we also have the probabilities given by the reference model. That is the original model. So here is where we don't want the model to change too much.

 

Now notice that we have this expected value, that's because we're averaging over all the responses. We have a lot of responses that we get evaluated, and the loss function is the average of all these.

 

Now why do we have a logarithm? When I see sums of logarithms, I like to see them as the logarithm of a product. And the product is normally of some numbers that are between 0 and 1. These are between 0 and 1 because you can see the sigmoid. So we could think of them as some probability of some event and the product is the probability of all the events independently. 

 

This is a trick I like to use when I see loss functions. I turn the summation of logarithm into logarithm of product and then, I imagine that product has to be the probability of many things happening at the same time. 

 

Now we want to maximize this probability which means, we want to maximize this sum over here. However, a loss funciton we normally want to minimize it. So why we minimize it? Because of this negative sign over here. So we're minimizing the negative. That means we're maximizing it. 

---

 

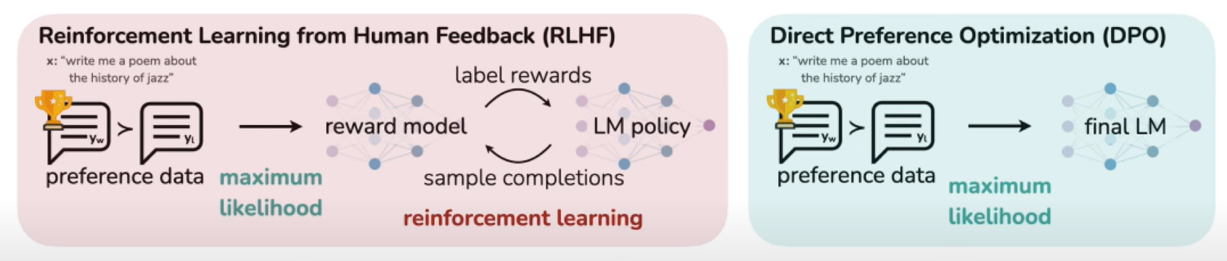
We have the Reinforcement Learning with Human Feedback which used two models. The Transformer model which is the policy model and the reward model which is the one that guesses the response from the human evaluator.

 

And we turn that into Direct Preference Optimization which only trains one neural network, the Transformer. It fine-tunes it using the elaborate loss function.

---